So berechnen sie die determinante einer 2×2-matrix

Auf dieser Seite erfahren Sie, was die Determinante einer 2×2-Matrix ist. Darüber hinaus finden Sie Schritt-für-Schritt-Lösungsbeispiele und Übungen zur Lösung von Determinanten 2. Ordnung, damit Sie es perfekt üben und verstehen können.

Was ist eine 2×2-Determinante?

Eine Determinante der Ordnung 2 ist eine Matrix der Dimension 2 × 2 , die durch einen vertikalen Balken auf jeder Seite der Matrix dargestellt wird. Wenn wir zum Beispiel die folgende Matrix haben:

\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}

Die Determinante der Matrix A wird wie folgt dargestellt:

\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}

Wie Sie gesehen haben, ist es einfach, die Determinante einer 2×2-Quadratmatrix zu schreiben. Schauen wir uns nun an, wie es berechnet wird:

Wie löst man eine Determinante der Ordnung 2?

Um die Determinante einer 2×2-Matrix zu berechnen, müssen wir die Elemente der Hauptdiagonale multiplizieren und das Produkt der Nebendiagonale subtrahieren.

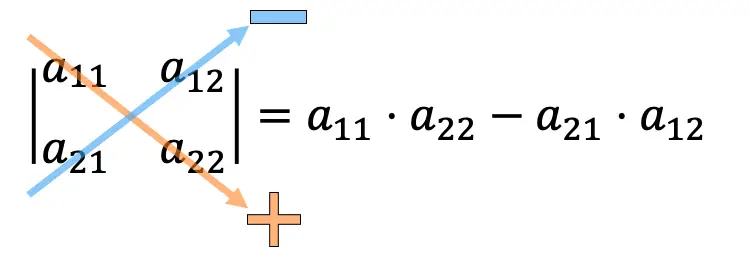
Beispiel für die Berechnung der Determinante einer 2x2-Matrix

Beispiele für die Berechnung von 2×2-Determinanten:

\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}

\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}

Probleme der Determinanten von 2 × 2-Matrizen gelöst

Übung 1

Berechnen Sie die folgende 2×2-Determinante:

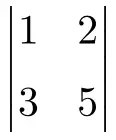
Übung Schritt für Schritt zur Determinante 2x2 gelöst

Um eine 2×2-Determinante zu erstellen, müssen Sie die Elemente der Hauptdiagonale multiplizieren und das Produkt der Nebendiagonale subtrahieren:

\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}

Übung 2

Lösen Sie die folgende Determinante der Dimension 2×2:

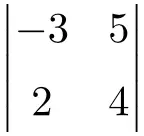
Schritt für Schritt gelöste Übungen zu 2x2 Determinanten

Um die Lösung einer Determinante 2. Ordnung zu finden, müssen Sie die Elemente der Hauptdiagonale multiplizieren und das Produkt der Nebendiagonale subtrahieren:

\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}

Übung 3

Finden Sie die Lösung für die folgende Determinante der Ordnung 2:

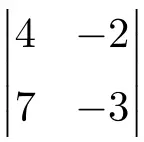
Übung Schritt für Schritt einer Determinante einer 2x2-Matrix gelöst

Um die Lösung einer Determinante der Dimension 2 zu finden, müssen Sie die Elemente der Hauptdiagonale multiplizieren und das Produkt der Nebendiagonale subtrahieren:

\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}

Übung 4

Berechnen Sie die folgende 2×2-Determinante:

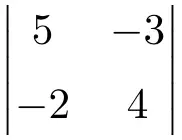
Wie man die Determinante einer 2x2-Matrix löst, Übung Schritt für Schritt gelöst

Um die Determinanten von 2×2-Matrizen zu berechnen, müssen wir die Elemente der Hauptdiagonale multiplizieren und das Produkt der Nebendiagonale subtrahieren:

\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}

Übung 5

Bestimmen Sie das Ergebnis der folgenden 2×2-Determinante:

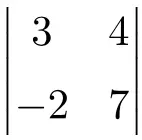
Übung zur schrittweisen Auflösung der Determinante einer Matrix 2. Ordnung gelöst

Um die Lösung einer 2×2-Determinante zu finden, müssen wir die Elemente der Hauptdiagonale multiplizieren und das Produkt der Nebendiagonale subtrahieren:

\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}

Hell! Sie wissen jetzt, wie Sie Determinanten der Dimension 2×2 erstellen! Jetzt können Sie sicher schon nachvollziehen, wie die 3×3-Determinante berechnet wird und auch, wie die Determinante einer 4×4-Matrix gelöst wird.

Kommentar verfassen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert

Nach oben scrollen