Multiplikation einer Zahl mit einer Matrix

Auf dieser Seite erfahren Sie, wie Sie eine Zahl mit einer Matrix multiplizieren. Sie haben auch Beispiele, die Ihnen helfen, es perfekt zu verstehen, und gelöste Übungen, damit Sie üben können. Außerdem finden Sie hier alle Eigenschaften des Produkts aus Skalar und Matrix.

Wie multipliziere ich eine Zahl mit einer Matrix?

Um eine Zahl mit einer Matrix zu multiplizieren , multiplizieren Sie jedes Element der Matrix mit der Zahl.

Beispiel:

Probleme bei der Multiplikation einer Zahl mit einer Matrix gelöst

Übung 1:

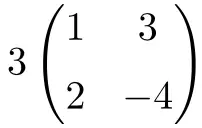
Gelöste Übung zum Produkt einer Zahl mit einer 2x2-Matrix, Operationen mit Matrizen

siehe Lösung

Es ist eine Multiplikation eines Skalars mit einer quadratischen Matrix der Ordnung 2:

$\displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}$

Übung 2:

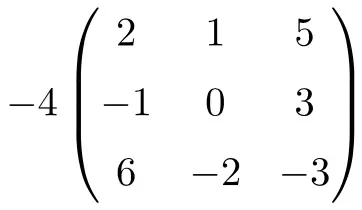
Schritt für Schritt gelöste Übung zur Multiplikation einer Zahl mit einer 3x3-Matrix, Operationen mit Matrizen

siehe Lösung

Es ist ein Produkt einer Zahl mit einer quadratischen Matrix der Ordnung 3:

$\displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}$

Übung 3:

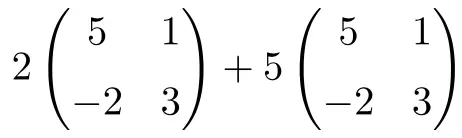
Gelöste Übung zur Multiplikation einer Zahl mit einer 2x2-Matrix, Operationen kombiniert mit Matrizen

siehe Lösung

Es handelt sich um eine Operation, die Produkte von Zahlen durch Matrizen und Summen von Matrizen der Dimension 2×2 kombiniert:

$\displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}$

Daher müssen wir zunächst nach Produkten auflösen:

$\displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}$

Und schließlich fügen wir die resultierenden Matrizen hinzu:

$\displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}$

Übung 4:

Betrachten Sie die folgenden Matrizen:

$\displaystyle A=\begin{pmatrix} 2 & -3 & 5 \\ 1 & 4 & 0 \\ -3 & 2 & -5 \end{pmatrix} \qquad B=\begin{pmatrix} 6 & 0 & 2 \\ -3 & 4 & 1 \\ 3 & 2 & 7 \end{pmatrix}$

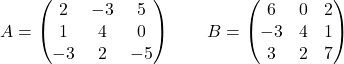
Berechnung:

$\displaystyle -2A+5I-3B$

siehe Lösung

Es handelt sich um eine Operation, die Skalarmultiplikationen mit Additionen und Subtraktionen von Matrizen der Dimension 3×3 kombiniert. Darüber hinaus die Matrix

$I$

ist die Identitätsmatrix, die sich aus 1 auf der Hauptdiagonale und 0 auf den restlichen Elementen zusammensetzt:

$\displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}$

Daher führen wir zunächst die Multiplikationen durch:

$\displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Wir fügen die ersten beiden Matrizen hinzu:

$\displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Abschließend führen wir die Subtraktion der Matrizen durch:

$\displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}$

Wenn diese Übungen zu Matrix-Skalarprodukten für Sie hilfreich waren, zögern Sie nicht, die Schritt-für-Schritt-Übungen zur Addition von Matrizen und zum Produkt von Matrizen zu üben, den beiden Arten von Matrixoperationen, die immer wiederkehren.

Eigenschaften des Produkts einer Zahl durch eine Matrix

Wie Sie wissen, gibt es viele Arten von Matrizen : quadratische Matrizen, dreieckige Matrizen, die Identitätsmatrix usw. Aber glücklicherweise gelten alle Eigenschaften des Produkts von Zahlen durch Matrizen für alle Matrizenklassen.

Hier sind die Eigenschaften der Multiplikation zwischen Skalaren und Matrizen:

Assoziative Eigenschaft:

$a \cdot (b \cdot A) = (a \cdot b) \cdot A$

Schauen Sie sich die folgenden zwei Operationen an, denn sie liefern das gleiche Ergebnis, egal wie wir 2 und 3 multiplizieren:

$\displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

$\displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

Verteilungseigenschaft bezüglich der Addition von Skalaren:

$(a+b) \cdot A = a \cdot A+ b \cdot A$

Wie Sie im Beispiel unten sehen können, ist es dasselbe, wenn wir zuerst 1+2 addieren und es dann mit einer Matrix multiplizieren, oder wenn wir die Matrix getrennt mit 1 und mit 2 multiplizieren und dann die Ergebnisse addieren:

$\displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

$\displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

Verteilungseigenschaft bezüglich der Matrixaddition:

$a \cdot \left(A + B \right) = a \cdot A + a \cdot B$

Mit anderen Worten: Die Addition zweier mathematischer Matrizen und deren anschließende Multiplikation mit einer Zahl entspricht der separaten Multiplikation der beiden Matrizen mit derselben Zahl und der anschließenden Addition der Ergebnisse. Im folgenden Beispiel können Sie Folgendes überprüfen:

$\displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

$\displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

Eigenschaft des neutralen Elements:

$1 \cdot A = A$

Wenn wir eine Matrix mit 1 multiplizieren, ändern wir daher die Matrix nicht:

$\displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}$

Dies sind alles Eigenschaften des Produkts aus einem Skalar und einer Matrix. Damit ist dieser Artikel abgeschlossen. Wir hoffen, dass es Ihnen gefallen hat und Sie vor allem gelernt haben, wie man die Multiplikation von Zahlen mit Matrizen löst.

Andererseits sind andere mit der Multiplikation verbundene und sehr nützliche Matrixoperationen Potenzen. Hier hinterlassen wir Ihnen die Seite, auf der Sie erfahren, was es ist und wie Sie die Leistung einer Matrix lösen können, falls Sie neugierig sind.

Eine zahl mit einer matrix multiplizieren

Wie multipliziere ich eine Zahl mit einer Matrix?

Beispiel:

Probleme bei der Multiplikation einer Zahl mit einer Matrix gelöst

Übung 1:

Übung 2:

Übung 3:

Übung 4:

Eigenschaften des Produkts einer Zahl durch eine Matrix

Kommentar verfassen Kommentieren abbrechen