Auf dieser Seite erfahren Sie, wie Sie Matrizen addieren und subtrahieren . Sie haben auch Beispiele, die Ihnen helfen, es perfekt zu verstehen, und gelöste Übungen, damit Sie üben können. Außerdem finden Sie hier alle Eigenschaften der Matrixaddition.
Wie addiere und subtrahiere ich Matrizen?
Um eine Addition (oder Subtraktion) zweier Matrizen zu berechnen, müssen Sie die Elemente addieren (oder subtrahieren), die dieselbe Position in den Matrizen einnehmen.
Beispiele:

Beachten Sie, dass zum Addieren oder Subtrahieren zweier Matrizen dieselbe Dimension haben müssen. Beispielsweise können die folgenden Matrizen nicht hinzugefügt werden, da die erste eine 2×2-Matrix und die zweite eine 3×2-Matrix ist:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-082c648e15685c4ddeac2cc2da502d96_l3.png)
Gelöste Aufgaben zur Addition und Subtraktion von Matrizen
Übung 1
Berechnen Sie die folgende Summe von 2×2-Matrizen:
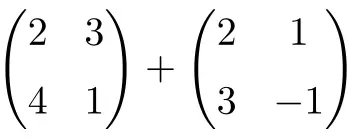
Es ist eine Summe zweier quadratischer Matrizen der Dimension 2×2:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d9428ad89a6bd149d5e63bc500879ac_l3.png)
Übung 2
Führen Sie die folgende Matrixsubtraktion durch:
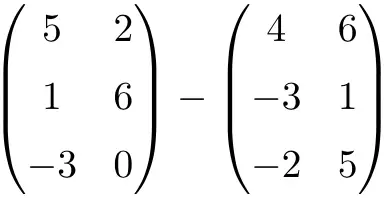
Es handelt sich um eine Subtraktion zweier Matrizen der Dimension 3×2:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c371e1f01df59f4b8abb018e476e66d7_l3.png)
Übung 3
Finden Sie das Ergebnis der folgenden Matrixsumme der Dimension 3×3:
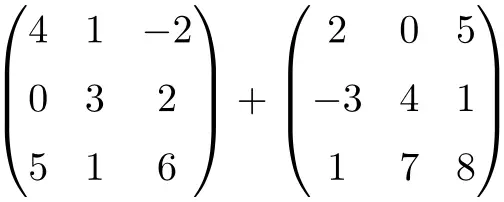
Es ist eine Summe zweier quadratischer Matrizen der Ordnung 3×3:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-280299cb0b37e1a585466c4570439ec4_l3.png)
Übung 4
Berechnen Sie die folgende Addition und Subtraktion quadratischer Matrizen der Ordnung 2:
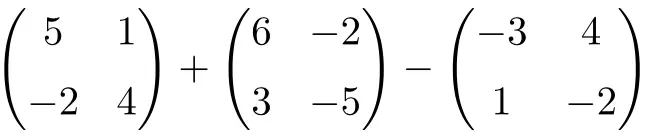
Es handelt sich um eine Operation kombiniert mit Addition und Subtraktion quadratischer Matrizen der Ordnung 2:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9fa4dba7699c0035ce5081756b4f62e_l3.png)
Also fügen wir zunächst die Matrizen auf der linken Seite hinzu:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e1544e4da9d5ad2ea3ec2e4ad0326023_l3.png)
Und dann berechnen wir die Subtraktion der Matrizen:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd7f32fc7c9429fdfc3b5b745e85975c_l3.png)
Übung 5
Lösen Sie die folgende Matrixaddition und -subtraktion:
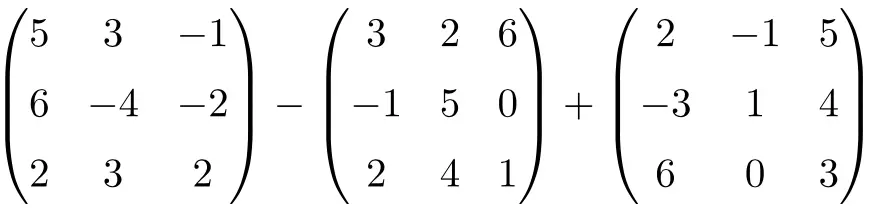
Es handelt sich um eine kombinierte Operation aus Subtraktion und Addition quadratischer Matrizen der Ordnung 3:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae66268adcd61258654056815542cf58_l3.png)
Zuerst lösen wir die Matrixsubtraktion:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4401b28babce2beaaa6f840c4ed8c959_l3.png)
Und schließlich fügen wir die Matrizen hinzu:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffba1ade3d98c434960b54fc0c7ffe1f_l3.png)
Nachdem Sie nun wissen, wie man Matrizen addiert und subtrahiert, ist es an der Zeit, sich mit der Multiplikation von Matrizen vertraut zu machen, der sicherlich wichtigsten Matrixoperation. Wie auf allen Seiten dieser Website finden Sie auch gelöste Schritt-für-Schritt-Matrixmultiplikationsübungen zum Üben. 😉
Matrixeigenschaften hinzufügen
Die Matrixaddition weist folgende Merkmale auf:
- Die Matrixaddition hat die kommutative Eigenschaft :
![]()
Daher ist die Reihenfolge, in der wir die Matrizen hinzufügen, dieselbe. Um dies zu demonstrieren, fügen wir zwei Matrizen hinzu, indem wir ihre Reihenfolge ändern, und Sie werden sehen, dass das Ergebnis dasselbe ist.
Wir fahren daher fort, zwei Matrizen in einer bestimmten Reihenfolge hinzuzufügen:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7eb454436dc3268ae8d6d2b62f395a7_l3.png)
Beachten Sie, dass das Ergebnis dasselbe bleibt, wenn wir die Reihenfolge der Addition der Matrizen umkehren:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c1e9cd77bc490913ed30ff63815da355_l3.png)
- Eine weitere Eigenschaft der Matrixaddition ist die des Gegenelements:
![]()
Mit anderen Worten, wenn wir eine Matrix plus dieselbe Matrix addieren, wobei alle ihre Elemente jedoch das Vorzeichen geändert haben, ist das Ergebnis eine Nullmatrix:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-add832e83fe554143cbd4c710315c1c0_l3.png)
- Die Matrixaddition hat auch die Eigenschaft eines neutralen Elements:
![]()
Diese Eigenschaft ist die offensichtlichste. Sie bezieht sich auf die Tatsache, dass jede Matrix plus einer Matrix voller Nullen derselben Matrix entspricht:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac7b0ba246075c196188798be2c6a034_l3.png)
- Die Matrixaddition hat die assoziative Eigenschaft:
![]()
Daher ist die Reihenfolge, in der wir die Matrizen hinzufügen, dieselbe. Schauen Sie sich das folgende Beispiel an, in dem wir drei Matrizen mit unterschiedlicher Reihenfolge hinzufügen und das Ergebnis das gleiche ist:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bae8e10bca43351f3a84f83bfe50ab55_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2cc2b7a14cacc7e403cd729cd863d309_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab1f88e74b139451eccb0471988c3db_l3.png)