Hier erfahren Sie, wie der Abstand einer Geraden zu einer Ebene berechnet wird und außerdem können Sie Beispiele und Übungen sehen, die Schritt für Schritt gelöst werden.
Wie groß ist der Abstand zwischen einer Linie und einer Ebene?
In der analytischen Geometrie hängt der Abstand zwischen einer Linie und einer Ebene im Raum von der relativen Position zwischen diesen beiden geometrischen Elementen ab:
- Wenn die Linie in der Ebene enthalten ist oder wenn die Linie und die Ebene parallel sind , ist der Abstand zwischen ihnen Null.
- Wenn die Linie parallel zur Ebene verläuft , wird der Abstand von der Linie zur Ebene ermittelt, indem man einen beliebigen Punkt auf der Linie nimmt und den Abstand von diesem Punkt zur Ebene berechnet.
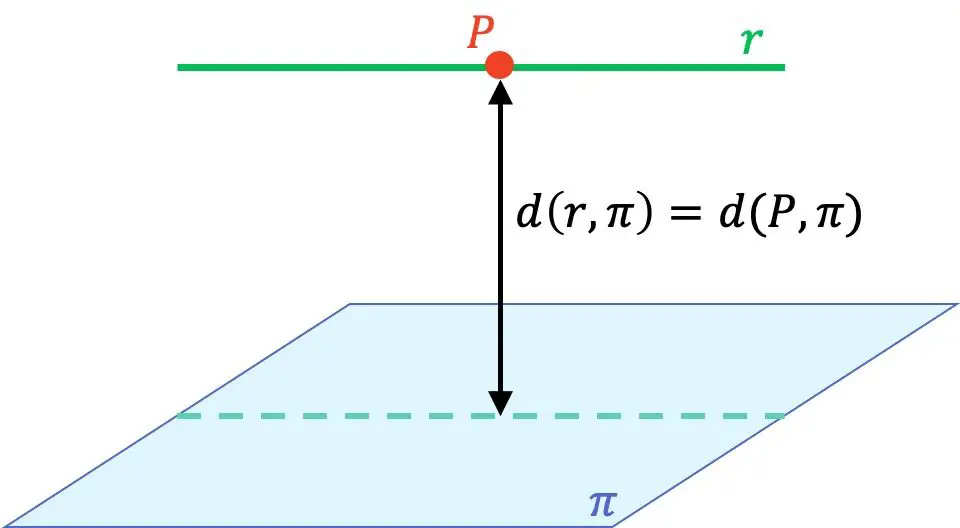
Um den Abstand einer Linie zu einer Ebene zu berechnen, ist es daher wichtig, dass Sie wissen, wie Sie die relative Position zwischen einer Linie und einer Ebene bestimmen und wie Sie den Abstand zwischen einem Punkt und einer Ebene berechnen. Wenn Sie also nicht ganz klar sind oder die Formeln nicht kennen, empfehlen wir Ihnen, zunächst einen Blick auf die verlinkten Seiten zu werfen, wo Sie Schritt für Schritt Erklärungen, Beispiele und gelöste Übungen finden.
Beispiel für die Berechnung des Abstands zwischen einer Linie und einer Ebene
Damit Sie sehen können, wie Sie den Abstand zwischen einer Geraden und einer Ebene im Raum (im R3) ermitteln, lösen wir beispielhaft eine Aufgabe:
- Wie weit ist die Linie?
im Flugzeug
?
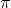
![\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4785f2386b4ff9387b56cf8c5645c62d_l3.png "Rendered by QuickLaTeX.com")
Um den Abstand zwischen der Linie und der Ebene zu ermitteln, müssen Sie zunächst die relative Position zwischen beiden kennen.
Einerseits wird die Linie in Form parametrischer Gleichungen definiert, ihr Richtungsvektor und ein Punkt, durch den sie verläuft, sind also:
![\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0765b71f9eead3b644fd5de150cdf321_l3.png "Rendered by QuickLaTeX.com")
Und andererseits ist der Vektor normal zur Ebene:
Um die relative Position zwischen der Ebene und der Linie zu bestimmen, muss daher das Skalarprodukt zwischen dem Richtungsvektor der Linie und dem Vektor normal zur Ebene berechnet werden:
![\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39d2d450c32a6fdf3182a3d16cc18116_l3.png "Rendered by QuickLaTeX.com")
Das Ergebnis des Skalarprodukts ist Null, die Gerade kann also nur in der Ebene enthalten oder parallel zu dieser sein. Um herauszufinden, um welchen Fall es sich handelt, setzen wir die kartesischen Koordinaten des Punktes auf der Geraden in die Gleichung der Ebene ein:
Indem wir den Punkt der Geraden in die Gleichung der Ebene einsetzen, erhalten wir eine Ungleichung, d. h. der Punkt respektiert die Gleichung der Ebene nicht und folglich sind die Gerade und die Ebene parallel.
Sobald wir wissen, dass die Linie und die Ebene parallel sind, können wir nun den geometrischen Abstand zwischen ihnen berechnen. Dazu nehmen wir den Punkt auf der Geraden und berechnen den Abstand von diesem Punkt zur Ebene.
Wir verwenden also die Formel für den Abstand von einem Punkt zu einer Ebene:
Jetzt setzen wir den Wert jeder Unbekannten in die Formel ein:
Und schließlich führen wir die Operationen durch:
Damit der Abstand zwischen der Linie und der Ebene dem Abstand zwischen dem Punkt und der Ebene entspricht, berechnet man:
Offensichtlich muss uns die Distanz immer einen positiven Wert geben, denn Distanzen sind immer positiv. Wenn wir ein negatives Ergebnis erhalten, bedeutet das, dass wir bei einem Schritt einen Fehler gemacht haben.