Hier erfahren Sie, wie der Winkel zwischen einer Linie und einer Ebene berechnet wird. Sie können sich auch Beispiele ansehen und zusätzlich mit Schritt für Schritt gelösten Übungen zu Winkeln zwischen Linien und Ebenen üben.
Wie groß ist der Winkel zwischen einer Geraden und einer Ebene?
Der Winkel zwischen einer Linie und einer Ebene ist der Winkel zwischen der Linie und ihrer orthogonalen Projektion auf die Ebene.
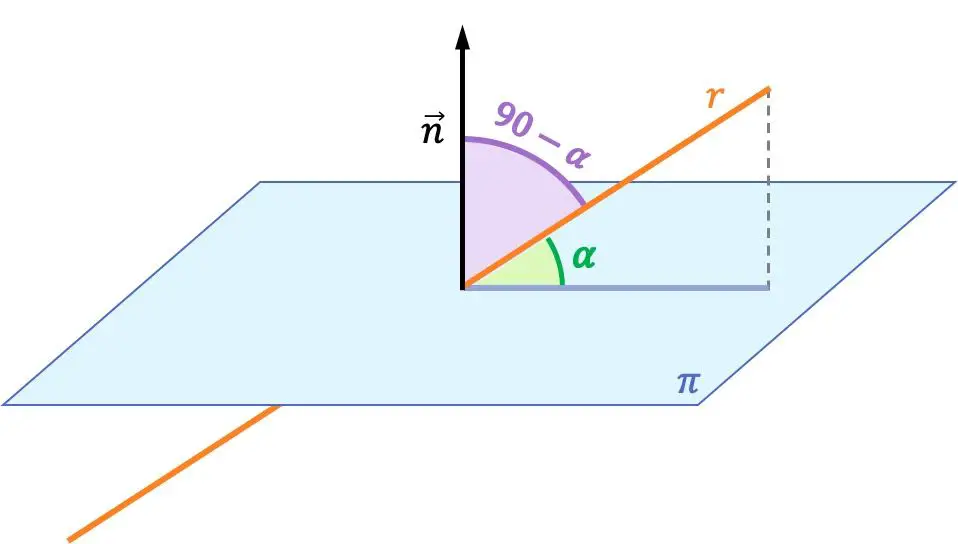
Der Winkel zwischen einer Linie und einer Ebene ist das Komplement des Winkels zwischen dieser Linie und dem Vektor normal zur Ebene. Daher wird der Winkel zwischen einer Linie und einer Ebene aus dem Winkel zwischen dem Richtungsvektor der Linie und dem Normalenvektor der Ebene berechnet.
Winkelformel zwischen einer Linie und einer Ebene
Um die Formel für den Winkel zwischen einer Ebene und einer Linie abzuleiten, müssen Sie wissen, wie man den Winkel zwischen zwei Vektoren ermittelt . Auf der verlinkten Seite finden Sie die Erklärung sowie Beispiele und Schritt für Schritt gelöste Übungen. Wenn Sie also nicht mehr wissen, wie es geht, empfehlen wir Ihnen, einen Blick darauf zu werfen.
Da also der Winkel zwischen einer Linie und einer Ebene komplementär zum Winkel zwischen dem Richtungsvektor dieser Linie ist
![]()
und der Normalenvektor zu dieser Ebene
![]()
Aus der Formel für den Winkel zwischen zwei Vektoren schließen wir, dass der Winkel zwischen einer Linie und einer Ebene dem folgenden Ausdruck entspricht:
![]()
Daher lautet die Formel für den Winkel zwischen einer Geraden und einer Ebene :
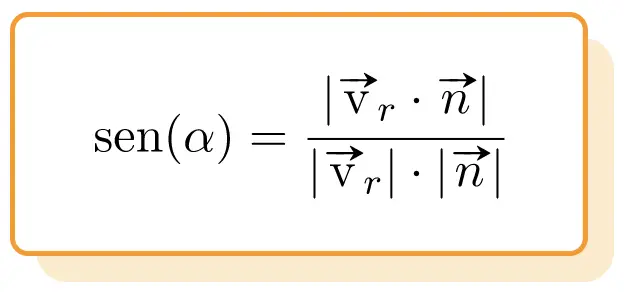
Gold:
-

ist der direkte Vektor der Geraden.
-
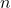
ist der Vektor normal zur Ebene.
Beispiel für die Berechnung des Winkels zwischen einer Linie und einer Ebene
Damit Sie sehen können, wie Sie ein solches Problem lösen können, finden Sie hier ein Beispiel für die Berechnung des Winkels zwischen einer Linie und einer Ebene:
- Berechnen Sie den Winkel, den die Linie bildet

mit dem Flugzeug
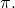
Ihre Gleichungen seien:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb8b61cb99a7af826a63ee098efc3a3c_l3.png)
Die Linie wird in Form parametrischer Gleichungen ausgedrückt, daher ist ihr Richtungsvektor:
![]()
Andererseits ist die Ebene in Form einer impliziten (oder allgemeinen) Gleichung definiert, sodass ihr Normalenvektor lautet:
![]()
Sobald wir also den Richtungsvektor der Linie und den Normalenvektor der Ebene kennen, wenden wir die Formel für den Winkel zwischen einer Linie und einer Ebene an:
![]()
Wir ersetzen die Vektoren in der Formel:
![]()
Und wir machen die Berechnungen:
![]()
![]()
![]()
![]()
Zum Schluss invertieren wir den Sinus mit dem Taschenrechner und ermitteln den Wert des Winkels:
![]()
Der Winkel zwischen der Geraden und der Ebene beträgt also etwa 51,80°.
Wir müssen berücksichtigen, dass, wenn wir jemals ein Ergebnis von 0° erhalten, dies bedeutet, dass die Linie und die Ebene parallel sind oder dass die Linie in der Ebene enthalten ist. Und wenn der Winkel 90° beträgt, bedeutet dies, dass die Linie und die Ebene senkrecht zueinander stehen.
Probleme des Winkels zwischen einer Linie und einer Ebene gelöst
Übung 1
Finden Sie den Winkel, den die Linie bildet
![]()
mit dem Flugzeug
![]()
Ihre Gleichungen seien:
![]()
![]()
Die Linie wird als kontinuierliche Gleichung ausgedrückt, daher ist ihr Richtungsvektor:
![]()
Andererseits hat die Ebene die Form einer impliziten (oder allgemeinen) Gleichung, sodass ihr Normalenvektor lautet:
![]()
Sobald wir also den Richtungsvektor der Linie und den Normalenvektor der Ebene kennen, verwenden wir die Formel für den Winkel zwischen einer Linie und einer Ebene:
![]()
![]()
![]()
![]()
![]()
![]()
Schließlich invertieren wir den Sinus und ermitteln den Wert des Winkels:
![]()
Daher beträgt der Winkel zwischen der Linie und der Ebene 4,10°.
Übung 2
Bestimmen Sie den Winkel, den die Linie bildet
![]()
mit dem Flugzeug
![]()
Ihre Gleichungen seien:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a8165b8e50fbc7764c77d1a984de353_l3.png)
![]()
Die Linie wird durch ihre impliziten (oder allgemeinen) Gleichungen ausgedrückt. Daher muss der Richtungsvektor der Linie ermittelt werden, indem das Vektorprodukt der Vektoren normal zu den beiden Ebenen berechnet wird, die die Linie bestimmen:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-54cc86087728e7e163034c95afc55286_l3.png)
![]()
Andererseits ist der Vektor normal zur Ebene:
![]()
Sobald wir also den Richtungsvektor der Linie und den Normalenvektor der Ebene kennen, verwenden wir die Formel für den Winkel zwischen einer Linie und einer Ebene:
![]()
![]()
![]()
![]()
![]()
Schließlich invertieren wir den Sinus und ermitteln den Wert des Winkels:
![]()
Daher beträgt der Winkel zwischen der Linie und der Ebene 46,33°.
Übung 3
Ermitteln Sie mithilfe der Formel für den Winkel zwischen einer Geraden und einer Ebene den Wert von
![]()
notwendig für das Recht
![]()
und das Flugzeug
![]()
parallel sein.
![]()
![]()
Erstens wird die Linie als Vektorgleichung ausgedrückt, sodass ihr Richtungsvektor lautet:
![]()
Andererseits hat die Ebene die Form einer allgemeinen Gleichung, sodass ihr Normalenvektor lautet:
![]()
Damit die beiden geometrischen Elemente parallel sind, muss der Winkel zwischen ihnen Null sein. Daher lautet die Formel für den Winkel zwischen einer Geraden und einer Ebene:
![]()
![]()
![]()
![]()
![]()
Daher muss das Skalarprodukt zwischen dem Richtungsvektor der Geraden und dem Normalenvektor Null sein. Und aus dieser Gleichung können wir den Wert der Unbekannten bestimmen
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wenn Sie diesen Artikel schließlich hilfreich fanden, sind Sie wahrscheinlich auch daran interessiert, wie man den Winkel zwischen zwei Ebenen ermittelt. Auf der Linkseite finden Sie eine sehr ausführliche Erklärung sowie die notwendige Formel zur Berechnung des Winkels zwischen zwei verschiedenen Ebenen. Darüber hinaus können Sie Beispiele und Übungen sehen, die Schritt für Schritt gelöst werden, um sie üben und verstehen zu können wie es perfekt gemacht wird.