Hier erfahren Sie, was rationale Funktionen sind. Darüber hinaus erklären wir, wie man den Definitionsbereich und die Asymptoten einer rationalen Funktion berechnet. Und nicht nur das, Sie werden auch alle Merkmale rationaler Funktionen sehen. Abschließend können Sie mit Schritt-für-Schritt-Übungen zu rationalen Funktionen üben.
Was ist eine rationale Funktion?
Die Definition einer rationalen Funktion lautet wie folgt:
Eine rationale Funktion ist eine Funktion, die durch den Quotienten zweier Polynome gebildet wird , d. h. eine rationale Funktion ist ein Bruch, dessen Zähler und Nenner ein Polynom haben.
Rationale Funktionen zeichnen sich durch Singularitäten an den Stellen aus, an denen der Nenner verschwindet.
![]()
Rationale Funktionen werden auch Bruchfunktionen genannt.
Andererseits sollten rationale Funktionen nicht mit irrationalen Funktionen verwechselt werden. Irrationale (oder radikale) Funktionen sind solche, die aus Wurzeln bestehen.
Beispiele für rationale Funktionen
Um den Begriff einer rationalen Funktion besser zu verstehen, sehen wir uns einige Beispiele dieser Art von Funktion an.
- Rationale Funktion mit einem Polynom ersten Grades im Zähler und Nenner:
![]()
Solche rationalen Funktionen werden auch Homographenfunktionen genannt.
- Rationale Funktion mit einer Konstante im Zähler und einem Polynom im Nenner:
![]()
Diese Arten rationaler Funktionen werden als inverse Proportionalitätsfunktionen bezeichnet und zur mathematischen Definition umgekehrt proportionaler Größen verwendet.
- Rationale Funktion mit einem Polynom dritten Grades im Zähler und einem Polynom zweiten Grades im Nenner:
![]()
Bereich einer rationalen Funktion
Eine durch 0 geteilte Zahl ist eine Unbestimmtheit, die Unendlich (∞) ergibt, sodass eine rationale Funktion immer existiert, es sei denn, der Nenner ist 0.
Daher besteht der Definitionsbereich einer rationalen Funktion aus allen reellen Zahlen mit Ausnahme von Werten, die den Nenner aufheben.
Um den Definitionsbereich einer rationalen Funktion zu erhalten, müssen wir also herausfinden, wann der Nenner 0 ist, da dieser Punkt der einzige ist, der nicht zum Definitionsbereich gehört
Sehen wir uns an, wie der Definitionsbereich einer rationalen Funktion berechnet wird, indem wir ein Beispiel lösen:
![]()
Wir setzen zunächst den Nenner auf 0 und lösen dann die resultierende Gleichung:
![]()
![]()
Wenn x also -2 ist, ist der Nenner 0 und die Funktion existiert daher nicht. Der Definitionsbereich der Funktion besteht daher aus allen reellen Zahlen außer x=-2. Dies wird wie folgt angegeben:
![]()
Asymptoten einer rationalen Funktion
Eine der Haupteigenschaften rationaler Funktionen sind ihre Asymptoten, da sie ihre grafische Darstellung bestimmen.
➤ Siehe: Grafische Darstellung einer Funktion
Die Asymptoten einer rationalen Funktion sind Linien, denen sich der Graph der Funktion auf unbestimmte Zeit annähert, die sie aber nie berührt.
Es gibt drei Arten von Asymptoten: vertikale Asymptoten, horizontale Asymptoten und schräge Asymptoten.
Unten sehen Sie die drei Arten von Asymptoten, die eine rationale Funktion in rot dargestellt haben kann.
Vertikale Asymptote einer rationalen Funktion

Horizontale Asymptote einer rationalen Funktion

Schräge Asymptote einer rationalen Funktion

Wie Sie sehen, ist die Bestimmung der Asymptote einer Funktion aus ihrem Graphen ziemlich einfach, aber die Berechnung der Asymptoten einer rationalen Funktion ohne deren Graphendarstellung ist ziemlich kompliziert. Aus diesem Grund empfehlen wir Ihnen, sich auf unserer Website anzusehen, wie die Asymptoten einer Funktion berechnet werden.
Merkmale einer rationalen Funktion
Rationale Funktionen haben die folgenden Eigenschaften:
![]()
- Wie wir oben gesehen haben, umfasst der Bereich rationaler Funktionen alle reellen Zahlen mit Ausnahme von Werten, die den Nenner des Bruchs aufheben.
- Im Allgemeinen umfasst der Bereich (oder Bereich) einer rationalen Funktion alle reellen Zahlen mit Ausnahme von Werten, bei denen die Funktion eine horizontale Asymptote aufweist.
- Rationale Funktionen sind in ihrem gesamten Bereich kontinuierlich. Mit anderen Worten, rationale Funktionen weisen Diskontinuitäten an Punkten auf, die nicht zu ihrem Bereich gehören.
- Die grafische Darstellung der meisten rationalen Funktionen besteht aus zwei Hyperbeln.
- Aus dem Polynomzähler lassen sich einige Regeln für die Asymptoten rationaler Funktionen ableiten.

und das Nennerpolynom
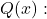
- Eine rationale Funktion hat eine vertikale Asymptote an den Punkten, die die Wurzeln von sind

aber das sind keine Wurzeln von
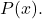
- Wenn der Grad von

ist kleiner als der Grad von

, die Linie y=0 ist eine horizontale Asymptote der rationalen Funktion.
- Wenn der Grad von

ist größer als der Grad von

, die rationale Funktion hat keine horizontale Asymptote.
- Wenn der Grad von

ist eine Einheit größer als der Grad von

und die beiden Polynome keine gemeinsame Wurzel haben, hat die rationale Funktion eine schiefe Asymptote.
- Eine rationale Funktion hat eine vertikale Asymptote an den Punkten, die die Wurzeln von sind
Gelöste Übungen zu rationalen Funktionen
Übung 1
Finden Sie den Definitionsbereich der folgenden rationalen Funktion:
![]()
Da es sich um eine rationale Funktion handelt, besteht der Definitionsbereich aus allen Zahlen mit Ausnahme derjenigen, die den Nenner aufheben, da die Funktion dann ∞ ergeben würde.
Also setzen wir den ganzzahligen Nenner gleich Null, um zu sehen, welche Zahl nicht zum Definitionsbereich gehört:
![]()
Und wir lösen die resultierende Gleichung:
![]()
![]()
Der Definitionsbereich der Funktion besteht daher nur aus Zahlen außer -2:
![]()
Übung 2
Finden Sie die Grenzwerte der folgenden rationalen Funktion mit den kartesischen Achsen:
![]()
Schnittpunkt mit X-Achse
Um den Schnittpunkt der Funktion mit der X-Achse zu finden, ist eine Lösung erforderlich
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wir haben zwei Lösungen der quadratischen Gleichung erhalten, sodass die rationale Funktion die Abszissenachse an zwei verschiedenen Punkten schneidet:
![]()
Schnittpunkt mit Y-Achse
Um den Schnittpunkt mit der Y-Achse zu finden, müssen Sie rechnen
![]()
![]()
Jede durch Null geteilte Zahl ist eine Unbestimmtheit, die Unendlich ergibt. Daher verläuft die rationale Funktion an keinem Punkt oberhalb der Y-Achse, das heißt, sie hat keinen Schnittpunkt mit der Y-Achse.
Übung 3
Zeichnen Sie die folgende rationale Funktion in ein Diagramm:
![]()
Als erstes muss der Definitionsbereich der Funktion berechnet werden:
![]()
![]()
![]()
![]()
Sobald wir den Definitionsbereich der Funktion kennen, erstellen wir eine Wertetabelle:

Zum Abschluss stellen Sie einfach die erhaltenen Punkte in einem Diagramm dar und zeichnen die Hyperbeln, um so die rationale Funktion zu zeichnen:

Übung 4
Bestimmen Sie die Asymptoten der unten dargestellten rationalen Funktion:
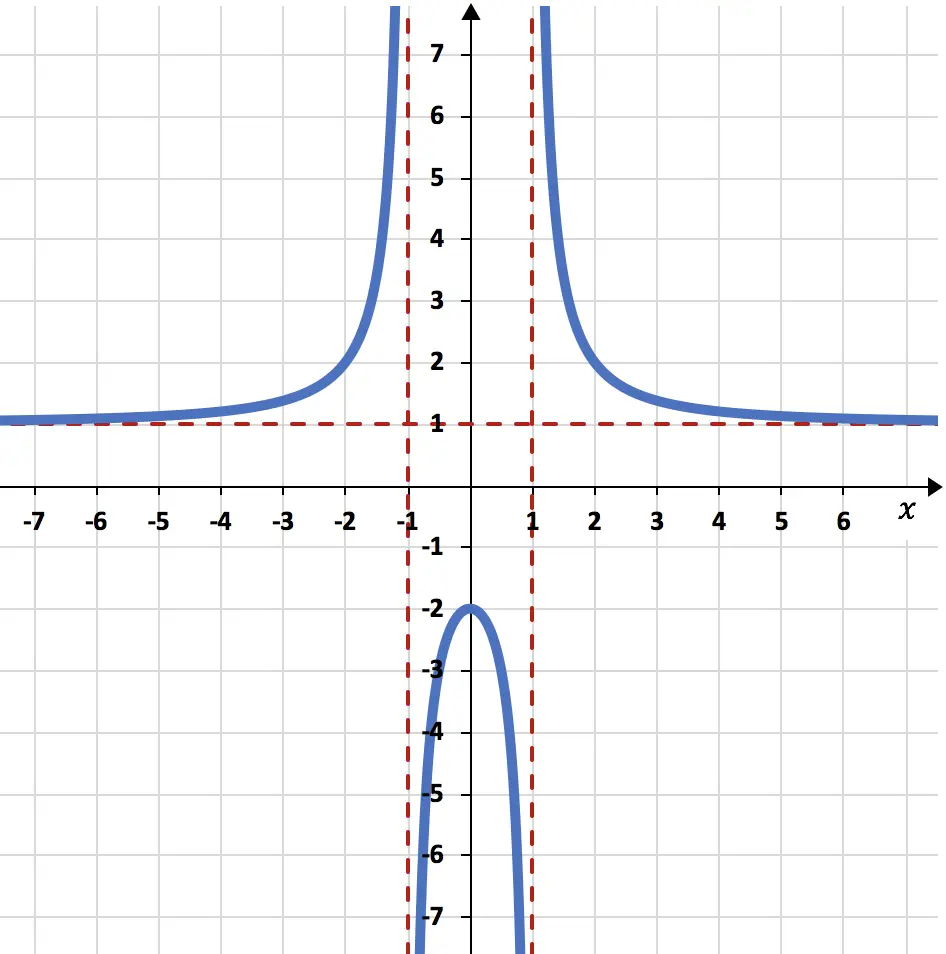
Die Asymptoten sind in der Grafik sehr deutlich sichtbar, da sie als rote gepunktete Linien dargestellt werden.
Bei diesem Problem liegt die Funktion sehr nahe an der horizontalen Linie y=1, berührt sie jedoch nie. Daher hat die rationale Funktion eine einzige horizontale Asymptote, nämlich y=1.
Ebenso liegt die grafische Darstellung der Funktion sehr nahe an den vertikalen Linien x=-1 und x=1, erreicht diese Werte jedoch nie. Die rationale Funktion hat daher zwei verschiedene vertikale Asymptoten, nämlich x=-1 und x=1.
Übung 5
Berechnen Sie alle Asymptoten der folgenden rationalen Funktion:
![]()
Hinweis: Um diese Übung zu lösen, empfehlen wir Ihnen, zunächst den Link oben zur Berechnung der Asymptoten einer Funktion aufzurufen und sich die Erklärung anzusehen.
vertikale Asymptote
Um die vertikalen Asymptoten einer Funktion zu berechnen, müssen wir zunächst den Definitionsbereich der Funktion ermitteln. Daher setzen wir den Nenner der rationalen Funktion gleich 0, um die Punkte zu finden, die nicht zum Definitionsbereich gehören:
![]()
![]()
![]()
Der Definitionsbereich der Funktion besteht daher aus allen Zahlen außer -1:
![]()
Also könnte x=-1 eine vertikale Asymptote sein. Um dies zu überprüfen, müssen wir den Grenzwert der Funktion an der Stelle berechnen:
![]()
Daher ist x=-1 eine vertikale Asymptote der rationalen Funktion, da der Grenzwert der Funktion an diesem Punkt Unendlich ergibt.
horizontale Asymptote
Um die horizontalen Asymptoten zu bestimmen, müssen wir den unendlichen Grenzwert der Funktion berechnen:
![]()
![]()
In diesem Fall ist das Ergebnis der unbestimmten Unendlichkeitsgrenze zwischen Unendlich die Division der Koeffizienten von x höchsten Grades, da Zähler und Nenner von gleicher Ordnung sind.
Die beiden unendlichen Grenzen der Funktion ergaben 3, also ist y=3 eine horizontale Asymptote der rationalen Funktion.
schräge Asymptote
Da es eine horizontale Asymptote gibt, hat die rationale Funktion keine schräge Asymptote.