Auf dieser Seite finden Sie eine Erklärung, was nebenläufige Leitungen sind, sowie Beispiele für nebenläufige Leitungen.
Was sind konkurrierende Linien?
Die mathematische Definition gleichzeitiger Linien lautet wie folgt:
In der Geometrie sind gleichzeitige Linien zwei oder mehr koplanare Linien , die sich im selben Punkt (dem sogenannten Parallelitätspunkt) schneiden. Daher hat eine Menge konkurrierender Geraden nur einen gemeinsamen Punkt.
Wenn wir in der Ebene (im R2) arbeiten, können zwei verschiedene Geraden nur zusammenfallen, parallel oder schneidend sein. Somit sind alle Sekantenlinien auch gleichzeitige Linien, da sie einen Schnittpunkt haben.
Wenn Ihnen das vorherige Konzept nicht klar war, empfehle ich Ihnen, einen Blick auf die Definition sich schneidender Linien zu werfen. Dort erfahren Sie, was diese Arten von Linien sind und wie Sie feststellen können, ob sich zwei Linien schneiden oder nicht.
Wenn wir andererseits im Raum (im R3) operieren, ist es schwieriger, konkurrierende Linien zu finden, da es komplizierter ist, dass sich 2, 3, 4, … Linien im selben Punkt schneiden und darüber hinaus im enthalten sind gleiches Flugzeug.
Andererseits gilt der Begriff des Wettbewerbs nicht nur für Linien: Wenn zwei oder mehr verschiedene geometrische Objekte einen gemeinsamen Punkt haben, bedeutet dies, dass sie Konkurrenten sind.
Beispiel konkurrierender Linien
Nachdem wir die Bedeutung gleichzeitiger Zeilen kennengelernt haben, schauen wir uns nun ein Beispiel für diesen Zeilentyp an:
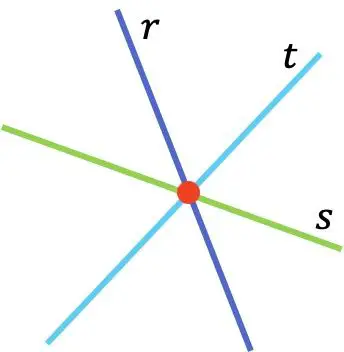
Wie Sie in der grafischen Darstellung der Linien r, s und t sehen können, sind die drei Linien gleichzeitig, da sie sich im selben Punkt schneiden (in Rot dargestellt).
Bevor wir jedoch fertig sind: Wenn Ihnen diese Seite gefallen hat, interessieren Sie sich möglicherweise auch für gerade Linien im Allgemeinen. Nun, ein sehr wichtiges Konzept über Linien ist die Berechnung ihrer Gleichung. Tatsächlich werden Liniengleichungen in der analytischen Geometrie sehr häufig verwendet. Wie diese Gleichung aussieht, können Sie auf der nächsten Seite sehen: So berechnen Sie die Gleichung der Geraden, die durch zwei Punkte verläuft .