Koplanare linien

Auf dieser Seite erfahren Sie, was es bedeutet, wenn zwei Geraden koplanar sind. Sie können auch sehen, wann zwei Linien koplanar sind, und außerdem finden Sie Beispiele und gelöste Aufgaben zu Koplanarlinien.

Was sind zwei Koplanarlinien?

In der analytischen Geometrie lautet die Definition koplanarer Linien wie folgt:

Zwei Linien sind koplanar, wenn sie in derselben Ebene liegen. Daher können koplanare Linien nur Sekantenlinien , parallele Linien oder zusammenfallende Linien sein.

Darüber hinaus reichen zwei Koplanarlinien aus, um eine Ebene vollständig zu definieren. Obwohl eine Ebene offensichtlich mehr als zwei Koplanarlinien haben kann, enthält jede Ebene tatsächlich unendlich viele Linien.

Wenn andererseits zwei Linien nicht koplanar sind, bedeutet dies, dass sie sich schneiden.

Beispiele für Koplanarlinien

Damit Sie das Konzept der Koplanarlinien besser verstehen, hier ein Beispiel mit drei Linien:

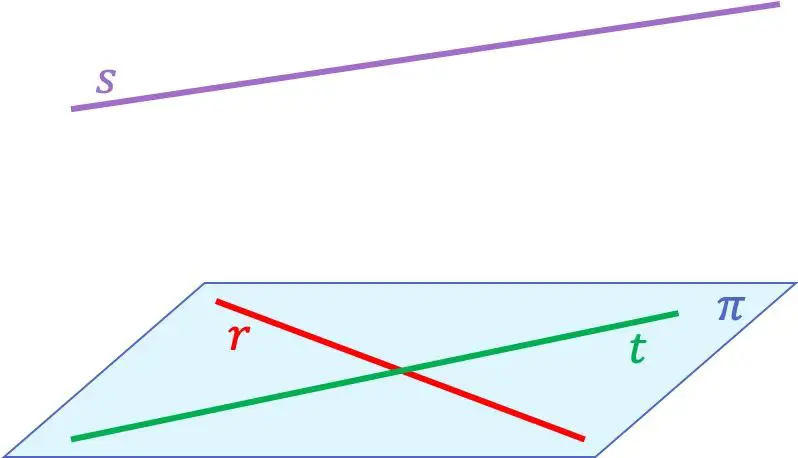
In diesem Fall die Zeilen

Und

Sie sind koplanar, weil sie zur gleichen Ebene gehören. Stattdessen die gerade Linie

ist mit keiner der beiden anderen Geraden koplanar, da sie die Geraden schneidet

Und

Woher wissen Sie, ob zwei Linien koplanar sind?

Wie wir oben bei der Erklärung der Koplanarlinien gesehen haben, kann es sich nur um Schnittlinien, parallele oder zusammenfallende Linien handeln. Mit anderen Worten, zwei gekreuzte Linien werden niemals koplanar sein.

Um zu wissen, ob zwei Linien koplanar sind, muss daher die relative Position zwischen ihnen bestimmt werden. Wenn es sich um zwei sich schneidende, parallele oder zusammenfallende Linien handelt, bedeutet dies, dass es sich um koplanare Linien handelt.

Um also die Koplanarität zweier Linien zu überprüfen, müssen Sie zunächst wissen, wie man die relative Position zweier Linien im Raum berechnet . Wenn Sie mit diesem Konzept noch nicht vertraut sind, schauen Sie sich am besten zunächst den Link an. Dort finden Sie die vollständige Erklärung sowie Beispiele, Übungen und gelöste Probleme.

Übung zu Koplanarlinien gelöst

Als Beispiel lösen wir eine typische Aufgabe zu Koplanaren:

• Bestimmen Sie, ob die folgenden zwei Linien koplanar sind oder nicht:

Als erstes müssen wir die relative Position zwischen den beiden Geraden ermitteln und dazu müssen wir beide mit der gleichen Art von Gleichung ausgedrückt haben. Dann überqueren wir die Gerade

von der allgemeinen (oder impliziten) Gleichung zu parametrischen Gleichungen:

Der Richtungsvektor jeder Geraden ist also:

Die Koordinaten der Richtungsvektoren der beiden Geraden sind proportional, es kann sich also nur um zusammenfallende oder parallele Geraden handeln. Daher besteht in diesem speziellen Fall keine Notwendigkeit, die genaue relative Position zu berechnen, da parallele Linien und zusammenfallende Linien koplanare Linien sind. Die beiden Geraden sind also koplanar .