Auf dieser Seite erfahren Sie, was die Exzentrizität der Ellipse bedeutet und wie sie berechnet wird (Formel). Darüber hinaus sehen Sie Beispiele für die Berechnung der Ellipsenexzentrizität.
Was ist die Exzentrizität der Ellipse?
Die Exzentrizität einer Ellipse ist ein Parameter, der misst, wie rund oder abgeflacht eine Ellipse ist. Das heißt, die Exzentrizität einer Ellipse gibt an, wie sehr die Ellipse einem Kreis ähnelt.
Andererseits erinnern wir uns auch daran, woraus eine Ellipse besteht: Die Ellipse ist der Ort aller Punkte einer Ebene, deren Summe der Abstände zu zwei anderen festen Punkten (genannt Brennpunkte F und F‘) konstant ist.
Ellipsen-Exzentrizitätsformel
Nachdem wir die Definition der Exzentrizität der Ellipse gesehen haben, sehen wir uns an, wie sie anhand ihrer Formel berechnet wird:
Die Formel für die Exzentrizität der Ellipse lautet wie folgt:
![]()
Gold:
-

ist die Exzentrizität der Ellipse
-

ist der Abstand von einem Brennpunkt (Punkte F und F‘) der Ellipse zu ihrem Mittelpunkt
-

ist die Länge der großen Halbachse (oder Hauptachse) der Ellipse.
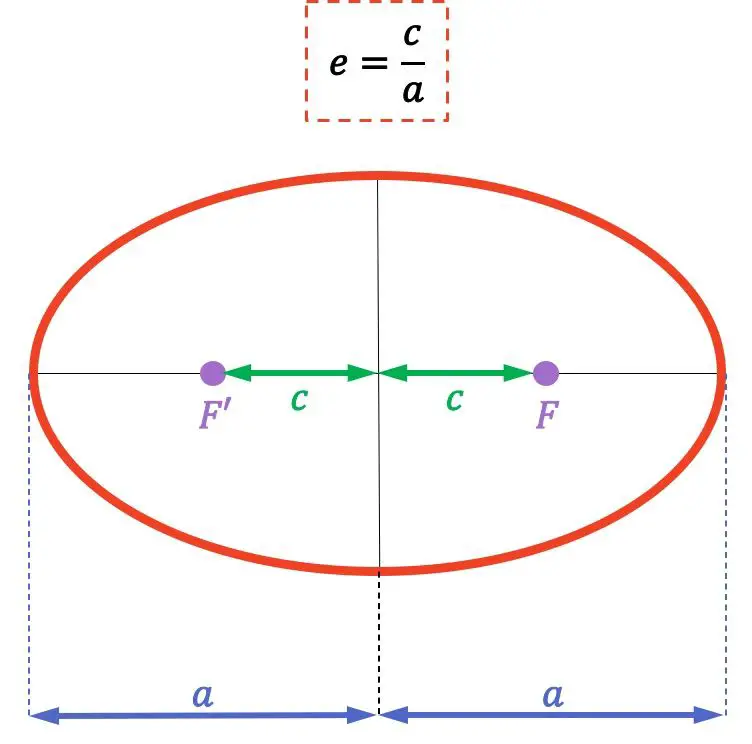
Denken Sie daran, dass die Brennpunkte einer Ellipse die festen Punkte sind, deren Summe der Abstände zu jedem Punkt auf der Ellipse konstant ist. Darüber hinaus wird der Abstand zwischen den beiden Brennpunkten als Brennweite bezeichnet.
Der Exzentrizitätswert reicht von Null, was bedeutet, dass es sich um einen perfekten Kreis handelt, bis zu Eins, was bedeutet, dass es sich um eine horizontale Linie handelt. Offensichtlich sind 0 und 1 nicht enthalten, da die resultierenden geometrischen Objekte keine Ellipsen mehr sind.

![]()
d(P,F)
![]()
d(P,F‘)
![]()
hat
![]()
hat

![]()
hat
![]()
vs,
![]()
e= \cfrac{c}{a} = \cfrac{4}{5} = \bm{0,8} $