Hier erfahren Sie, wie die Ellipsengleichung (Formel) berechnet wird, unabhängig davon, ob sie den Ursprung als Mittelpunkt hat oder nicht. Außerdem erfahren Sie, was die Elemente der Ellipse sind, wie man sie berechnet und wofür sie verwendet werden. Darüber hinaus können Sie sich Beispiele und gelöste Aufgaben zu Ellipsengleichungen ansehen.
Ellipsengleichungsformel
Die Formel für die Gleichung der Ellipse in kartesischen Koordinaten lautet:
![]()
Gold:
-

Und

sind die Koordinaten des Mittelpunkts der Ellipse:
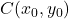
-

ist der horizontale Radius der Ellipse.
-

ist der vertikale Radius der Ellipse.
Gleichung der im Ursprung zentrierten Ellipse
Eine sehr häufige Art von Ellipse ist eine, deren Mittelpunkt im Koordinatenursprung liegt, also im Punkt (0,0). Deshalb werden wir sehen, wie man die Gleichung der Ellipse findet, deren Mittelpunkt im Ursprung liegt.
Folgen Sie der Formel für die Ellipsengleichung:
![]()
Wenn die Ellipse auf dem Koordinatenursprung zentriert ist, bedeutet dies Folgendes
![]()
Und
![]()
sind gleich 0, also lautet Ihre Gleichung:
![]()
Es gibt Mathematiker, die diesen Ausdruck auch kanonische Gleichung oder reduzierte Gleichung der Ellipse nennen.
Elemente der Ellipse
Sobald wir sehen, wie die Gleichung der Ellipse aussieht, werden wir sehen, was ihre Elemente sind. Aber erinnern wir uns zunächst daran, was genau eine Ellipse ist:
Die Ellipse ist eine flache, geschlossene, gekrümmte Linie, die dem Umfang sehr ähnlich ist, ihre Form jedoch eher oval ist. Insbesondere ist die Ellipse der Ort aller Punkte einer Ebene, deren Summe der Abstände zu zwei anderen festen Punkten (genannt Brennpunkte F und F‘) konstant ist.
Die Elemente einer Ellipse sind also:
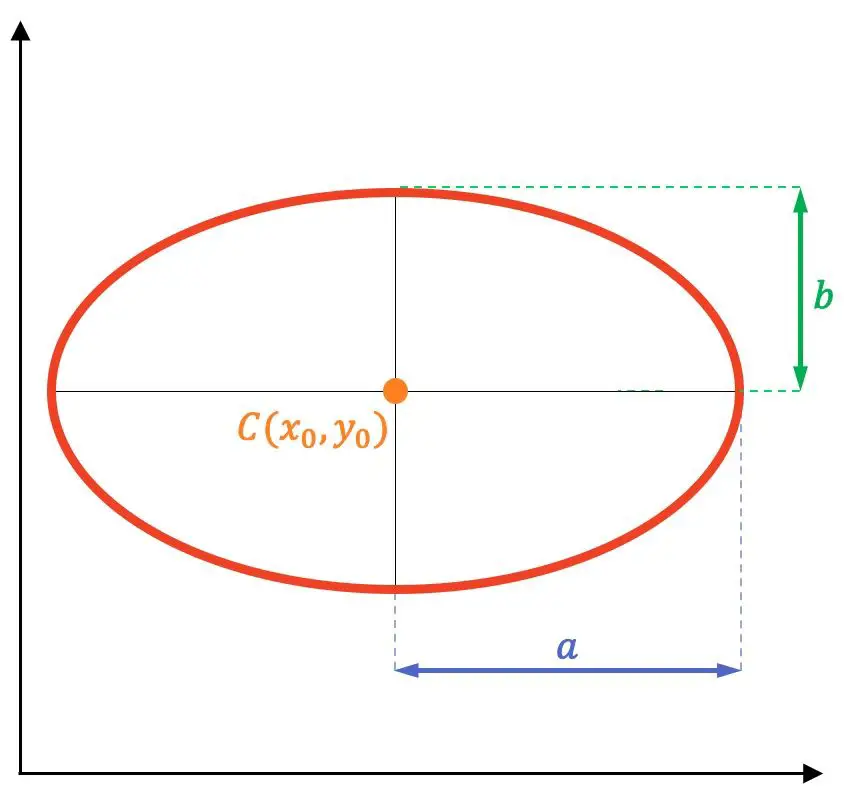
- Die Brennpunkte : Dies sind die Fixpunkte F und F‘ (lila gefärbte Punkte im Bild unten). Die Summe der Abstände zwischen jedem Punkt auf der Ellipse und jedem Fokus ist für alle Punkte auf der Ellipse konstant.
- Haupt- oder Brennachse : Dies ist die Symmetrieachse der Ellipse, in der sich die Brennpunkte befinden. Auch Hauptachse genannt.
- Sekundärachse : Dies ist die Symmetrieachse der Ellipse senkrecht zur Hauptachse. Sie wird auch Nebenachse genannt und entspricht der Mittelsenkrechten des Segments, das die Brennpunkte verbindet.
- Mittelpunkt : ist der Schnittpunkt der Achsen der Ellipse. Außerdem ist es das Symmetriezentrum der Ellipse (orangefarbener Punkt im Diagramm).
- Eckpunkte : Schnittpunkte der Ellipse mit ihren Symmetrieachsen (schwarze Punkte).
- Halbgroße Achse oder Hauptachse: Segment, das vom Mittelpunkt der Ellipse bis zu den Scheitelpunkten der Hauptachse reicht.
- Kleine Halbachse oder Nebenachse: Segment zwischen dem Mittelpunkt der Ellipse und den Scheitelpunkten der Nebenachse.
- Brennweite : Dies ist der Abstand zwischen den beiden Brennpunkten.
- Halbbrennweite : entspricht der Entfernung zwischen der Mitte und jedem der Brennpunkte.
- Die Radiovektoren sind die Segmente, die jeden Punkt der Ellipse mit jedem Fokus verbinden (blaue Segmente im Diagramm).

Beziehung zwischen Elementen einer Ellipse
Die verschiedenen Elemente einer Ellipse sind miteinander verknüpft. Darüber hinaus sind die Beziehungen zwischen ihnen für Übungen zu Ellipsen sehr wichtig, da sie normalerweise zum Lösen von Problemen auf Ellipsen und zur Bestimmung ihrer Gleichungen erforderlich sind.
Wie wir oben bei der Definition der Ellipse gesehen haben, ist der Abstand von jedem Punkt auf der Ellipse zum Brennpunkt F plus der Abstand vom gleichen Punkt zum Brennpunkt F‘ konstant. Nun, dieser konstante Wert entspricht dem Doppelten dessen, was die große Halbachse misst. Mit anderen Worten, die folgende Gleichung gilt für jeden Punkt auf einer Ellipse:
![]()
Gold
![]()
Und
![]()
ist der Abstand vom Punkt P zum Fokus F bzw. F‘ und
![]()
ist die Länge der Halbbrennachse.
Da der Scheitelpunkt der Sekundärachse genau in der Mitte der Brennachse liegt, entspricht der Abstand von diesem zu einem der Brennpunkte der Länge der Halbprimärachse (
![]()
):
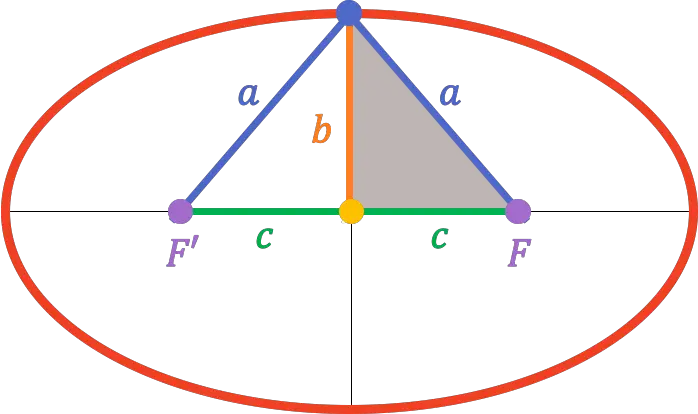
Aus dem Satz des Pythagoras lässt sich also die Beziehung ermitteln, die zwischen der Haupthalbachse, der Nebenhalbachse und der Halbbrennweite besteht:
![]()
Denken Sie an diese Formel, da sie für die Berechnung der Ergebnisse von Übungen mit Ellipsen sehr nützlich ist.
Exzentrizität der Ellipse
Natürlich sind nicht alle Ellipsen gleich, aber einige sind länger und andere flacher. Es gibt also einen Koeffizienten, der misst, wie rund eine bestimmte Ellipse ist. Dieser Koeffizient wird Exzentrizität genannt und mit der folgenden Formel berechnet:
![]()
Gold
![]()
ist der Abstand vom Mittelpunkt der Ellipse zu einem ihrer Brennpunkte und
![]()
die Länge der großen Halbachse.
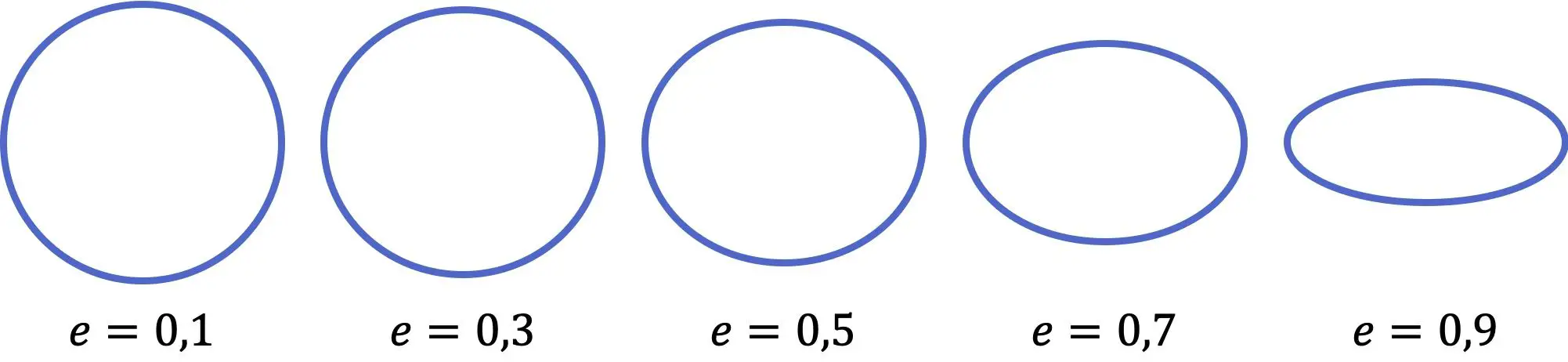
Wie Sie in der vorherigen Darstellung sehen können, ähnelt die Ellipse umso mehr einem Kreis, je kleiner der Wert der Exzentrizität ist. Andererseits gilt: Je größer der Koeffizient, desto abgeflachter ist die Ellipse. Darüber hinaus reicht der Exzentrizitätswert von Null (perfekter Kreis) bis Eins (horizontale Linie), beides nicht inklusive.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1 C(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}

![]()
d(P,F) + d(P,F‘)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Wenn dieser Artikel für Sie hilfreich war, werden Sie sicherlich auch an unseren Seiten zur Hyperbelformel und zur Parabelformel interessiert sein. Sie finden eine detaillierte Erklärung, was die Hyperbel und die Parabel sind, ihre Gleichungen, ihre Eigenschaften, Beispiele, gelöste Aufgaben, …