Winkel zwischen zwei Linien (Formel)

Auf dieser Seite finden Sie die Erklärung, wie Sie den Winkel zwischen zwei Geraden berechnen (Formel). Sie können sich auch einige Beispiele ansehen und darüber hinaus mit Schritt für Schritt gelösten Übungen üben.

Wie groß ist der Winkel zwischen zwei Geraden?

Der Winkel zwischen zwei Geraden ist der kleinste Winkel zwischen diesen beiden Geraden.

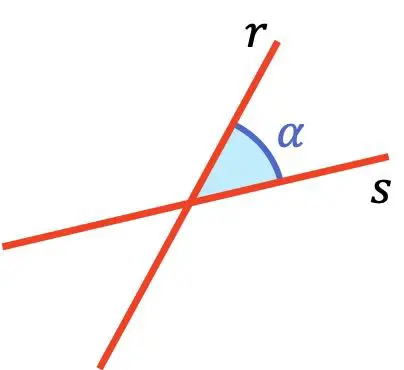
Im Plan gibt es vier Arten von Linien, je nachdem, welchen Winkel sie zwischen ihnen bilden: sich schneidende Linien (zwischen 0° und 90°), senkrechte Linien (90°), parallele Linien (0°) und zusammenfallende Linien (0°).

Schnittlinien

Winkel zwischen zwei sich schneidenden Linien

Schnittlinien schneiden sich in einem spitzen Winkel zwischen 0° und 90°.

Senkrechte gerade Linien

Senkrechte Linien schneiden sich im rechten Winkel von 90°.

Parallele Linien

Parallele Linien berühren sich nie und bilden zwischen sich einen Winkel von 0°.

zusammenfallende Linien

Zwei zusammenfallende Geraden haben alle Punkte gemeinsam und daher besteht zwischen ihnen immer ein Winkel von 0°.

Zusammenfassend lässt sich sagen, dass die Berechnung des Winkels zwischen zwei parallelen, zusammenfallenden oder senkrechten Linien unmittelbar erfolgt: Die parallelen Linien und die zusammenfallenden Linien bilden einen Winkel von 0 Grad, da sie die gleiche Richtung haben, und die senkrechten Linien schneiden sich in einem Winkel von 90 Grad . Um andererseits den Winkel zwischen zwei sich schneidenden Linien zu ermitteln, müssen Sie eine Formel anwenden (wir werden sie weiter unten sehen).

Wie berechnet sich der Winkel zwischen zwei Geraden?

Es gibt zwei Möglichkeiten, den Winkel zwischen zwei Linien zu berechnen. Die erste Methode verwendet den Richtungsvektor jeder Linie und die zweite Methode basiert auf der Steigung jeder Linie.

Keines der Verfahren ist besser als das andere, tatsächlich sind beide recht einfach, aber je nachdem, wie die Zeilen ausgedrückt werden, ist die eine oder andere Methode praktisch. Wir empfehlen Ihnen daher, sich mit der Anwendung beider mathematischer Methoden vertraut zu machen.

Ausrichtungsmethode für Linienvektoren

Die Formel zur Berechnung des Winkels zwischen zwei Geraden anhand ihrer Richtungsvektoren lautet:

Gegeben seien die Richtungsvektoren zweier verschiedener Geraden:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

Der Winkel zwischen diesen beiden Linien kann mit der folgenden Formel berechnet werden:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Gold

$\lvert \vv{\text{u}} \rvert$

Und

$\lvert \vv{\text{v}} \rvert$

sind die Module der Vektoren

$\vv{\text{u}}$

Und

$\vv{\text{v}}$

jeweils.

Denken Sie daran, dass die Formel für die Größe eines Vektors lautet:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Sehen wir uns anhand eines Beispiels an, wie man den Winkel zwischen zwei Linien ermittelt:

Berechnen Sie den Winkel zwischen den folgenden beiden Geraden:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

Um den Winkel zwischen den beiden Linien zu berechnen, müssen Sie zunächst den Richtungsvektor jeder Linie ermitteln.

das Recht

$r$

wird in Form einer parametrischen Gleichung ausgedrückt, daher sind die Komponenten des Vektors, der seine Richtung angibt:

$\vv{r} = (-3,4)$

und das Gesetz

$\displaystyle s$

ist in Form einer impliziten (oder allgemeinen) Gleichung definiert, daher sind die Koordinaten seines Richtungsvektors:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Da wir nun den Richtungsvektor jeder Linie kennen, können wir die Formel für den Winkel zwischen zwei Linien verwenden:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Wir bestimmen daher den Betrag der beiden Vektoren:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

Wir führen die Vektoroperationen der Winkelformel durch:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

Und schließlich berechnen wir den Winkel, den die beiden Geraden mit dem Kehrwert des Kosinus bilden:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

Denken Sie daran, dass Sie den Kehrwert des Kosinus mit dem Taschenrechner mit der Taste berechnen können

$\boxed{\cos ^{-1}}.$

Steigungsmethode

Um diese Methode zu verstehen, müssen Sie natürlich die Steigung der Geraden kennen. Sie können dieses Konzept unter dem Link nachlesen. Dort finden Sie eine detaillierte Erklärung seiner Bedeutung, seiner Berechnung, Beispiele und gelöste Übungen zur Steigung einer Linie.

Die Formel zur Berechnung des Winkels zwischen zwei Geraden aus deren Steigungen lautet:

Oder zwei unterschiedliche Zeilen:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

Der Winkel zwischen diesen beiden Linien kann mit der folgenden Formel ermittelt werden:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Gold

$m_1$

Und

$m_2$

sind die Steigungen der Linien

$r_1$

Und

$r_2$

jeweils.

Sehen wir uns anhand eines Beispiels an, wie man den Winkel zwischen zwei Geraden anhand ihrer Steigungen berechnet:

Finden Sie den Winkel zwischen den folgenden zwei Linien:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

Die Steigung jeder Linie ist die Zahl vor der Variablen

$x:$

$m_r = 4$

$m_s = -3$

Daher kann der Winkel zwischen den beiden Linien durch Anwendung der Steigungsformel ermittelt werden:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

Und schließlich finden wir den Winkel mit der Umkehrung der Tangente:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

Denken Sie daran, dass Sie den Kehrwert der Tangente mit dem Taschenrechner mit der Taste berechnen können

$\boxed{\tan ^{-1}}.$

Wir haben gerade ein Beispiel gesehen, bei dem die Steigungen zweier Geraden als explizite Gleichung ausgedrückt wurden. Wenn sie jedoch die Form einer Punktsteigungsgleichung hätten, müsste das gleiche Verfahren verwendet werden.

Winkelprobleme zwischen zwei Linien lösen

Übung 1

Bestimmen Sie den Winkel, den die folgenden zwei Geraden bilden:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

siehe Lösung

In diesem Fall verwenden wir die Richtungsvektormethode. Daher müssen wir zunächst den Richtungsvektor jeder Linie ermitteln. Beide Linien werden als parametrische Gleichungen ausgedrückt, sodass die Komponenten ihrer Richtungsvektoren die Terme vor dem Parameter sind

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

Da wir nun den Richtungsvektor jeder Linie kennen, können wir die Formel für den Winkel zwischen zwei Linien verwenden:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Wir bestimmen daher den Betrag der beiden Vektoren:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

Wir lösen das Skalarprodukt zwischen den beiden Vektoren des Zählers und der Multiplikation der Module des Nenners:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

Und schließlich ermitteln wir den Winkel, den die beiden Geraden bilden, indem wir den Kosinus umkehren:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Übung 2

Finden Sie den Winkel zwischen den folgenden zwei Linien:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

siehe Lösung

Wir werden dieses Problem mit der Richtungsvektormethode lösen, also müssen wir zuerst den Richtungsvektor jeder Linie finden. das Recht

$r$

wird in Form einer allgemeinen (oder impliziten) Gleichung ausgedrückt, sodass die Komponenten des Vektors, der seine Richtung markiert, sind:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

und das Gesetz

$\displaystyle s$

ist in Form einer kontinuierlichen Gleichung definiert, daher sind die kartesischen Koordinaten seines Richtungsvektors die Zahlen der Nenner:

$\vv{s} = (6,3)$

Sobald wir den Richtungsvektor jeder Linie kennen, können wir die Formel für den Winkel zwischen zwei Linien verwenden:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Wir bestimmen daher die Module der beiden Vektoren:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

Wir führen die Operationen zwischen Vektoren der Winkelformel durch:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

Und schließlich berechnen wir den Winkel, den die beiden Geraden mit dem Kehrwert des Kosinus bilden:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Übung 3

Wie groß ist der Winkel zwischen den folgenden beiden Linien?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

siehe Lösung

In diesem Fall verwenden wir die Methode der Steigungen der Linien, um den Winkel zu ermitteln, den sie bilden, da die Linien die Form einer expliziten Gleichung haben.

Die Steigung jeder Linie ist die Zahl, die die unabhängige Variable begleitet

$x:$

$m_r = -2$

$m_s = 5$

Daher kann der Winkel zwischen den beiden Linien durch Anwendung der Steigungsformel bestimmt werden:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

Und schließlich ermitteln wir den Winkel zwischen den beiden Geraden, indem wir die Tangente umkehren:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Übung 4

Finden Sie die Gleichung der Geraden, die durch den Punkt verläuft

$P(5,-1)$

und bildet mit der Linie einen Winkel von 45°

$r.$

Sei gesagt Zeile:

$\displaystyle r: \ y=2x+4$

siehe Lösung

Um das Problem zu lösen, rufen wir an

$s$

rechts, die wir berechnen werden. Darüber hinaus verwenden wir die Steigungsmethode, da wir die Steigung der Linie kennen

$r:$

$m_r=2$

Aus der Formel für den Winkel zwischen zwei Geraden (Steigungsmethode) können wir den Wert der Steigung der Geraden ermitteln

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

Wir setzen die bekannten Werte in die Formel ein:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

Und wir versuchen, die resultierende Gleichung zu lösen:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

Der absolute Wert der Gleichung macht es etwas schwierig, sie zu lösen, da Sie sowohl die positiven als auch die negativen Optionen analysieren müssen:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

Wir haben daher zwei mögliche Lösungen: eine Linie mit einer Steigung von -3 und eine weitere Linie mit einer Steigung von einem Drittel.

Die Formel für die Punkt-Steigungsgleichung einer Geraden lautet:

$y-y_0=m(x-x_0)$

Sobald wir also die Steigung der beiden möglichen Geraden kennen, können wir die Punkt-Steigungsgleichung jeder Geraden mit dem Punkt schreiben, durch den sie gemäß der Aussage verlaufen müssen:

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

Winkel zwischen zwei linien (formel)

Wie groß ist der Winkel zwischen zwei Geraden?

Wie berechnet sich der Winkel zwischen zwei Geraden?

Ausrichtungsmethode für Linienvektoren

Steigungsmethode

Winkelprobleme zwischen zwei Linien lösen

Übung 1

Übung 2

Übung 3

Übung 4

Kommentar verfassen Kommentieren abbrechen