Auf dieser Seite finden Sie alles über die explizite Gleichung einer Geraden: Was ist das, wie lautet ihre Formel, Berechnungsbeispiele usw. Außerdem finden Sie eine ausführliche Erläuterung der Bedeutung von Steigung und des Achsenabschnitts der expliziten Gleichung. Darüber hinaus sehen Sie verschiedene Beispiele und können anhand von Schritt für Schritt gelösten Übungen üben.
Wie lautet die explizite Gleichung der Geraden?
Denken Sie daran, dass die mathematische Definition einer Linie eine Menge aufeinanderfolgender Punkte ist, die in derselben Richtung ohne Kurven oder Winkel dargestellt werden.
Die explizite Liniengleichung ist also eine Möglichkeit, jede Linie mathematisch auszudrücken. Dazu müssen Sie lediglich die Steigung der Linie und den Punkt kennen, an dem sie die Y-Achse schneidet.
Formel für die explizite Gleichung der Geraden
Die Formel für die explizite Gleichung der Geraden lautet:
![]()
Gold
![]()
ist die Steigung der Geraden und
![]()
sein y-Achsenabschnitt, also die Höhe, in der er die Y-Achse schneidet.
Sehen wir uns anhand eines Beispiels an , wie die explizite Gleichung der Geraden berechnet wird :
- Schreiben Sie die explizite Gleichung der Geraden, die durch den Punkt verläuft
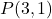
und Steigung m=2.
Die Formel für die explizite Gleichung der Geraden lautet:
![]()
In diesem Fall sagt uns die Aussage, dass die Steigung der Geraden m=2 ist, sodass die Gleichung der Geraden wie folgt lautet:
![]()
Es reicht daher aus, den Koeffizienten n zu berechnen. Dazu müssen wir einen Punkt, der zur Geraden gehört, in ihre Gleichung einsetzen. Und in diesem Fall sagt uns die Aussage, dass die Gerade durch den Punkt verläuft
![]()
Noch:
![]()
![]()
Und wir lösen die resultierende Gleichung, um den Wert von n zu finden:
![]()
![]()
![]()
![]()
Die explizite Gleichung der Geraden lautet daher:
![]()
Bedenken Sie, dass es neben der expliziten Gleichung auch andere Möglichkeiten gibt, eine Linie analytisch auszudrücken. Zum Beispiel die Vektorgleichung , bei der es sich um eine Art Liniengleichung handelt, die sich von allen anderen unterscheidet, da der Richtungsvektor und ein Punkt auf der Linie durch ihre eigenen Koordinaten ausgedrückt werden. Im Link können Sie sehen, was es ist und warum es so besonders ist.
Bedeutung der Parameter m und n
Wie wir in der Definition der expliziten Gleichung der Geraden gesehen haben, ist der Parameter
![]()
ist die Steigung der Geraden und
![]()
sein y-Achsenabschnitt. Aber was bedeutet das? Sehen wir uns dies anhand der grafischen Darstellung einer Linie an:

Der Begriff unabhängig
![]()
ist der Schnittpunkt der Linie mit der Computerachse (OY-Achse). In der Grafik oben
![]()
ist gleich 1, da die Linie die y-Achse bei y=1 schneidet.
Andererseits der Begriff
![]()
gibt die Steigung der Geraden an , also ihre Neigung. Wie Sie in der Grafik sehen können,
![]()
ist gleich 2, da die Linie um 2 vertikale Einheiten für 1 horizontale Einheit ansteigt.
Offensichtlich nimmt die Funktion zu, wenn die Steigung positiv ist (steigt), wenn die Steigung negativ ist, nimmt die Funktion ab (sinkt).
Berechnen Sie die Steigung einer Geraden
Darüber hinaus gibt es drei verschiedene Möglichkeiten, die Steigung einer Geraden numerisch zu bestimmen:
- Gegeben seien zwei unterschiedliche Punkte auf der Geraden

Und

Die Steigung der Geraden ist gleich:
- Ja

ist der Richtungsvektor der Geraden, ihre Steigung ist:
- Ja

ist der Winkel, den die Linie mit der Abszissenachse (X-Achse) bildet, die Steigung der Linie entspricht dem Tangens dieses Winkels:
![]()
![]()
![]()

Relative Position der Linien
Schließlich wird die Steigung einer Geraden auch genutzt, um die Beziehung zwischen mehreren Geraden zu kennen. Da zwei parallele Geraden die gleiche Steigung haben und andererseits die Steigung einer Geraden der negative Kehrwert der Steigung einer anderen Geraden ist, bedeutet dies, dass diese beiden Geraden senkrecht zueinander stehen.


Berechnen Sie die explizite Gleichung der Geraden, die durch zwei Punkte verläuft
Ein sehr typisches Problem besteht darin, die explizite Gleichung einer Geraden anhand zweier Punkte zu finden, durch die sie verläuft. Sehen wir uns anhand eines Beispiels an, wie es gelöst wird:
- Bestimmen Sie die explizite Gleichung der Geraden, die durch die folgenden zwei Punkte verläuft:
![]()
Um die explizite Gleichung der Geraden zu finden, müssen Sie den Wert der Parameter m und n kennen. Wir berechnen also zunächst die Steigung der Geraden mit der Doppelpunktformel:
![]()
![]()
Und dann können wir den y-Achsenabschnitt finden, indem wir einen Punkt auf der Geraden in die Gleichung einsetzen:
![]()
![]()
![]()
![]()
![]()
Die explizite Gleichung der Geraden lautet also:
![]()
Finden der expliziten Gleichung aus der impliziten Gleichung
Schließlich besteht ein weiteres Problem, auf das wir häufig stoßen, darin, die explizite Gleichung der Geraden aus ihrer impliziten Gleichung (auch allgemeine oder kartesische Gleichung genannt) zu finden. Um die folgende Methode zu verstehen, müssen Sie natürlich genau wissen, wie die implizite Gleichung lautet und wie sie lautet. Aber wenn Sie sich überhaupt nicht daran erinnern, können Sie es im Link nachlesen.
Wenn Sie also bereits die implizite (oder allgemeine) Gleichung einer Geraden beherrschen, sehen wir uns an, wie dieses Verfahren funktioniert:
- Finden Sie die explizite Gleichung der folgenden Zeile:
![]()
Um die explizite Gleichung der Geraden zu finden, müssen wir lediglich nach der Variablen auflösen
![]()
Also geben wir die Bedingungen ohne weiter
![]()
auf der anderen Seite der Gleichung:
![]()
Jetzt löschen wir die Variable
![]()
![]()
Und zum Schluss vereinfachen wir:
![]()
![]()
![]()
Die Steigung dieser Geraden beträgt also
![]()
und sein y-Achsenabschnitt ist 4.
Explizite Gleichungsprobleme gelöst
Übung 1
Geben Sie die Steigung und den y-Achsenabschnitt der folgenden Geraden an:
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3077643710747855c7b59a93551fbad8_l3.png)
Die explizite Gleichung einer Geraden folgt der folgenden Formel:
![]()
Gold
![]()
ist die Steigung und
![]()
Der Computer am Ursprung. Noch:
![Rendered by QuickLaTeX.com \bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f62bc45bc23ea6c323b1a5d95ba40ca2_l3.png)
![Rendered by QuickLaTeX.com \bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-683f74baf43275be7565fc744704e6ed_l3.png)
![Rendered by QuickLaTeX.com \bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39e8a1c6dbe8e5ff8db1fc8b08c4c95d_l3.png)
Die letzte Zeile wird durch ihre implizite Gleichung ausgedrückt, daher müssen wir sie zunächst an eine explizite Gleichung übergeben (auflösen nach).
![]()
) dann können wir die Parameter identifizieren:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{cases} m = -2 \\[2ex] n=3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50c2bb75ae362e0a2dee3a3670459df3_l3.png)
Übung 2
Finden Sie die explizite Gleichung der Geraden, die durch den Punkt verläuft
![]()
und hat die Steigung
![]()
Die Formel für die explizite Gleichung der Geraden lautet:
![]()
In diesem Fall muss die Steigung der Geraden -2 betragen, sodass die Geradengleichung die folgende Form hat:
![]()
Es reicht daher aus, den Koeffizienten n zu berechnen. Dazu müssen Sie einen Punkt, der zur Geraden gehört, in deren Gleichung einsetzen und die resultierende Gleichung lösen:
![]()
![]()
![]()
![]()
![]()
Kurz gesagt lautet die explizite Gleichung der Geraden:
![]()
Übung 3
Finden Sie die explizite Gleichung der Geraden, die durch die folgenden zwei Punkte verläuft:
![]()
Um die explizite Gleichung der Geraden zu finden, müssen Sie den Wert der Parameter m und n kennen. Wir berechnen daher zunächst die Steigung der Geraden aus den Koordinaten der beiden Punkte:
![]()
![]()
Und dann bestimmen wir den Achsenabschnitt, indem wir einen Punkt auf der Geraden in die Gleichung einsetzen:
![]()
![]()
![]()
![]()
Die explizite Gleichung der Geraden lautet also:
![]()
Übung 4
Berechnen Sie die explizite Gleichung der Linie, die mit der X-Achse einen Winkel von 45° bildet und durch den Koordinatenursprung verläuft.
Wenn die Linie mit der OX-Achse einen Winkel von 45 Grad bildet, beträgt ihre Steigung:
![]()
![]()
Und sobald wir die Steigung der Linie kennen, können wir den y-Achsenabschnitt berechnen, indem wir einen Punkt auf der Linie in die Gleichung einsetzen. Darüber hinaus sagt uns die Anweisung, dass die Linie durch den Koordinatenursprung verläuft, was bedeutet, dass sie durch den Punkt (0,0) verläuft. Noch:
![]()
![]()
![]()
Die explizite Gleichung der Geraden lautet also:
![]()
Übung 5
Finden Sie die explizite Gleichung der Geraden parallel zur Geraden
![]()
und was passiert über den Punkt hinweg
![]()
gerade sein
![]()
![]()
Damit die Linie parallel zur Linie ist
![]()
beide müssen die gleiche Steigung haben, also:
![]()
![]()
Und sobald wir die Steigung der Linie kennen, können wir den y-Achsenabschnitt berechnen, indem wir den Punkt, der zur Linie gehört, in die Gleichung einsetzen:
![]()
![]()
![]()
![]()
![]()
Die explizite Gleichung der Geraden lautet also:
![]()
Übung 6
Was ist die explizite Gleichung jeder graphischen Linie?

blau rechts
Die blaue Linie erhöht sich jeweils um ein Y
![]()
rechts grün
Die grüne Linie erhöht sich für jedes
![]()
rote Linie
Die rote Linie nimmt für jedes X um zwei Y ab, sodass ihre Steigung -2 beträgt. Und die Linie schneidet die y-Achse bei y=-2, sodass ihr y-Achsenabschnitt ebenfalls -2 ist.
![]()