Was ist lineare regression?

Die lineare Regression ist eine statistische Methode zur Untersuchung der Beziehung zwischen zwei kontinuierlichen Variablen . Die Hauptidee der linearen Regression besteht darin, die gerade Linie zu finden, die am besten zu den Daten passt. Darüber hinaus können Sie den Wert einer Variablen anhand des Werts einer anderen vorhersagen.

Diese Gerade wird „Regression“ genannt und dient dazu, unbekannte Werte vorherzusagen oder die Beziehung zwischen Variablen zu verstehen. Zusammenfassend ist die lineare Regression ein Werkzeug zur Analyse und Modellierung der Beziehung zwischen zwei kontinuierlichen Variablen.

Warum ist lineare Regression wichtig?

Die lineare Regression ist wichtig, da Sie damit die Beziehung zwischen zwei kontinuierlichen Variablen modellieren und analysieren können, was für die Vorhersage zukünftiger Werte und die Identifizierung von Mustern und Trends in Daten nützlich sein kann.

Darüber hinaus ist die lineare Regression ein grundlegendes Werkzeug in der Statistik und den meisten Bereichen der wissenschaftlichen und sozialen Forschung, darunter unter anderem Wirtschaftswissenschaften, Psychologie, Medizin, Ingenieurwesen und Physik. Es wird auch bei der betriebswirtschaftlichen Entscheidungsfindung und Prozessoptimierung in Industrie und Wirtschaft eingesetzt.

Zusammenfassend ist die lineare Regression ein leistungsstarkes und vielseitiges Werkzeug, das die Analyse und ein besseres Verständnis von Daten und Beziehungen zwischen Variablen in verschiedenen Bereichen der Forschung und Praxis ermöglicht .

Welche Arten der linearen Regression gibt es?

Es gibt verschiedene Arten der linearen Regression, darunter:

einfache lineare Regression

Die einfache lineare Regressionsanalyse ist ein weit verbreitetes Werkzeug zur Untersuchung der Auswirkung einer unabhängigen Variablen auf eine einzelne abhängige Variable , wobei davon ausgegangen wird, dass zwischen ihnen eine lineare Beziehung besteht. Die einfache lineare Regressionsgleichung ermöglicht es uns, die Werte der abhängigen Variablen basierend auf den Werten der unabhängigen Variablen zu schätzen.

Die einfache lineare Regressionsformel lautet:

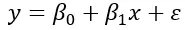
Dabei ist β ₀ der Wert der abhängigen Variablen, wenn die unabhängige Variable Null ist. β ₁ stellt die Änderung der abhängigen Variablen pro Einheitsänderung der unabhängigen Variablen dar und ε stellt das Residuum oder den Fehler dar. Das heißt, die Variabilität der Daten, die nicht durch die lineare Beziehung der Formel erklärt werden kann.

Multiple lineare Regression

Multiple lineare Regression wird verwendet, wenn es mehr als eine unabhängige Variable gibt, die sich auf die untersuchte abhängige Variable auswirken kann .

Die Formel für die multiple lineare Regression lautet:

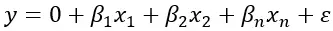
Dabei stellt Y _die abhängige Variable dar _{, β 1} , β ₂ , β _n sind die unabhängigen Variablen, die den Wert von Y beeinflussen können, die Regression und ε stellt den möglichen vorhandenen Fehler dar. Mit dieser Formel können wir den Wert von Y basierend auf den Werten der unabhängigen Variablen schätzen.

Was ist die lineare Regressionsformel?

Die lineare Regressionsformel lautet:

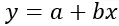
Gold:

y ist die abhängige Variable (oder Antwort), die vorhergesagt werden soll

x ist die unabhängige (oder Prädiktor-)Variable, die zur Erstellung der Vorhersage verwendet wird

a ist der Achsenabschnitt (oder der Punkt, an dem die Regressionsgerade die Y-Achse schneidet, wenn x=0)

b ist die Steigung der Regressionsgeraden (gibt die Änderungsrate von y für jede Änderung von x an)

Um die Werte von a und b zu ermitteln, verwenden wir die Methode der kleinsten Quadrate , die darauf abzielt, die Summe der quadratischen Fehler zwischen den beobachteten Werten und den durch die Regressionsgerade vorhergesagten Werten zu minimieren.

Hier sind die Formeln:

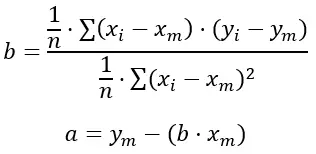
Gold:

n ist die Gesamtzahl der Datensätze, die wir haben.

x _i und y _i sind die Werte, die wir in der Summierung annehmen.

x _m und y _m sind die Durchschnittswerte jeder Variablen.

Wie wendet man die lineare Regressionsmethode an?

Die lineare Regressionsmethode kann wie folgt angewendet werden:

1. Daten sammeln : Als Erstes müssen Sie die Daten sammeln , die Sie interessieren. Wenn Sie beispielsweise den Zusammenhang zwischen dem Gehalt und dem Alter einer Gruppe von Personen untersuchen möchten, müssen Sie Informationen über das Gehalt und das Alter jeder einzelnen Person sammeln.
2. Plotten Sie die Daten – Als Nächstes müssen Sie die Daten auf einer kartesischen Ebene grafisch darstellen, wobei die unabhängige Variable (in diesem Fall das Alter) auf der horizontalen Achse und die abhängige Variable (Gehalt) auf der vertikalen Achse platziert wird.
3. Bestimmen Sie die Regressionsgerade : Es muss die Regressionsgerade ermittelt werden, die am besten zu den Daten passt. Diese Linie ergibt sich aus der linearen Regressionsformel, die anhand der statistischen Stichprobendaten berechnet wird.
4. Bewerten Sie die Anpassungsgüte – Es ist wichtig zu beurteilen, wie gut die Regressionslinie zu den Daten passt. Dies kann mithilfe statistischer Messungen erfolgen.
5. Vorhersagen treffen – Schließlich können mithilfe der resultierenden Regressionsgeraden Vorhersagen getroffen werden. Wenn Sie beispielsweise das Gehalt einer 30-jährigen Person vorhersagen möchten, würden Sie die lineare Regressionsformel verwenden und den Wert des Alters darin einsetzen.

Es ist wichtig zu beachten, dass diese Schritte je nach Art der verwendeten linearen Regression und der verwendeten Statistiksoftware leicht variieren können.

Wozu dient die lineare Regression?

Die lineare Regression wird verwendet, wenn Sie die Beziehung zwischen zwei Variablen analysieren möchten, wobei eine Variable den Wert einer anderen Variablen beeinflussen kann. Daher kann die lineare Regression verwendet werden, um zu verstehen, wie eine unabhängige Variable eine abhängige Variable beeinflusst, und um den Wert der abhängigen Variablen basierend auf der unabhängigen Variablen vorherzusagen.

Es ist wichtig zu beachten, dass die lineare Regression davon ausgeht, dass die Beziehung zwischen den beiden Variablen linear ist , was bedeutet, dass die Änderung der abhängigen Variablen proportional zur Änderung der unabhängigen Variablen ist.

Daher sollte die lineare Regression verwendet werden, wenn ein linearer Zusammenhang zwischen den beiden Variablen vermutet wird. Wenn diese Bedingung nicht erfüllt ist, ist es möglicherweise sinnvoller, andere nichtlineare Regressionsmodelle oder andere statistische Methoden zu verwenden.

Welche Anwendungen bietet die lineare Regression?

Die lineare Regression wird in einer Vielzahl von Anwendungen unter anderem in Bereichen wie Statistik, Wirtschaft, Ingenieurwesen, Sozialwissenschaften und Biologie eingesetzt. Hier sind einige der häufigsten Anwendungen der linearen Regression:

• Trendanalyse – Zur Analyse von Trends in historischen Daten und zur Vorhersage zukünftiger Trends.
• Prognose – Vorhersage des zukünftigen Werts einer Variablen basierend auf vergangenen Werten einer oder mehrerer Variablen.
• Marktforschung : Untersuchung des Zusammenhangs zwischen der Nachfrage nach einem Produkt und seinem Preis.
• Finanzanalyse – Untersuchung der Beziehung zwischen den Einnahmen und Ausgaben eines Unternehmens und Prognose zukünftiger Finanzergebnisse.
• Epidemiologische Studien : Untersuchen Sie den Zusammenhang zwischen der Exposition gegenüber einem Risikofaktor und der Wahrscheinlichkeit, eine Krankheit zu entwickeln.
• Sozialwissenschaften – Untersuchung der Beziehung zwischen zwei oder mehr Variablen in Bereichen wie Psychologie, Soziologie und Politikwissenschaft.
• Operations Research – Lineare Regression wird zur Modellierung und Optimierung komplexer Systeme in Bereichen wie Wirtschaftsingenieurwesen und Logistik eingesetzt.
• Umweltwissenschaften – werden zur Untersuchung der Beziehung zwischen Umweltfaktoren und Auswirkungen auf Ökosysteme verwendet.

Was sind Residuen in der linearen Regression?

Die Residuen in der linearen Regression sind die Differenz zwischen den beobachteten Werten der abhängigen Variablen und den vom linearen Regressionsmodell vorhergesagten Werten . Mit anderen Worten: Es handelt sich um den vertikalen Abstand zwischen den tatsächlichen Datenpunkten und der Regressionsgeraden.

Die Idee hinter Residuen besteht darin, dass die Residuen klein und zufällig sein sollten, wenn die Regressionsgerade gut zu den Daten passt. Wenn die Residuen groß sind oder einem bestimmten Muster folgen, kann dies ein Zeichen dafür sein, dass die Beziehung zwischen den Variablen nicht linear ist oder dass das lineare Regressionsmodell nicht an die Daten angepasst ist.

Residuen werden auch verwendet, um die Genauigkeit des linearen Regressionsmodells zu bewerten und Ausreißer oder einflussreiche Datenpunkte zu identifizieren, die sich auf die Qualität des Modells auswirken können.

Kann ich eine lineare Regression mit mehr als einer abhängigen Variablen ausführen?

Bei der linearen Regression ist die abhängige Variable immer eine einzelne Variable. Sie können jedoch mehr als eine unabhängige Variable haben. In diesem Fall würden wir von multipler linearer Regression sprechen .

Bei der multiplen linearen Regression besteht das Ziel darin, die Wirkung mehrerer unabhängiger Variablen auf eine einzelne abhängige Variable zu untersuchen.

Wie kann ich Koeffizienten in der linearen Regression interpretieren?

Bei der linearen Regression stellen die Koeffizienten die Steigung und den Achsenabschnitt der Regressionsgeraden dar. Die Steigung gibt die Änderung der abhängigen Variablen pro Einheitsänderung der unabhängigen Variablen an, während der Achsenabschnitt den Wert der abhängigen Variablen darstellt, wenn die unabhängige Variable gleich Null ist.

Numerische Beispiele für lineare Regression

Ein einfaches Beispiel könnte das Folgende sein:

Angenommen, wir haben die folgenden Alters- und Größendaten für eine Gruppe von Personen:

Alter)	Höhe (cm)
25	170
30	175
35	180
40	185
Vier fünf	190

Wir wollen herausfinden, ob es einen Zusammenhang zwischen dem Alter und der Körpergröße dieser Menschen gibt. Dazu verwenden wir die lineare Regression.

Zunächst können wir mit den Daten einstatistisches Diagramm zeichnen (in diesem Fall empfehlen wir die Verwendung eines Streudiagramms):

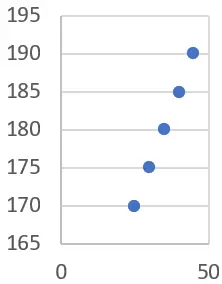
Wir können sehen, dass es einen klaren Trend gibt, dass mit zunehmendem Alter auch die Körpergröße zunimmt. Wir können dies bestätigen, indem wir die lineare Regressionsgerade berechnen.

Durch die Berechnung der Koeffizienten der linearen Regressionsgeraden mit den Formeln, die wir zuvor gesehen haben, erhalten wir:

bei = 145

b = 1

Daher lautet die Gleichung der linearen Regressionsgeraden:

Größe = 145 + 1 Alter

Mit dieser Gleichung können wir die Körpergröße einer Person anhand ihres Alters vorhersagen. Wenn eine Person beispielsweise 32 Jahre alt ist, können wir vorhersagen, dass sie folgende Größe haben wird:

Höhe = 145 + 1 32 = 177 cm