Absoluter Fehler und relativer Fehler sind zwei Maße zur Bewertung der Genauigkeit einer Berechnung oder Schätzung.
Der absolute Fehler bezieht sich auf die Differenz zwischen dem tatsächlichen Wert und dem geschätzten Wert . Der relative Fehler wiederum bezieht sich auf das Verhältnis zwischen dem absoluten Fehler und dem tatsächlichen Wert.
Beides ist wichtig, weil es Aufschluss über die Richtigkeit und Relevanz der Ergebnisse gibt. Darüber hinaus werden sie in vielen Bereichen eingesetzt, darunter im Ingenieurwesen, in der Physik und in den Wirtschaftswissenschaften. Wir beschreiben sie nachfolgend.
Was ist der absolute Fehler?
Der absolute Fehler ist ein Maß für die Differenz zwischen einem gemessenen oder geschätzten Wert und dem tatsächlichen Wert.
Es wird durch die Formel dargestellt: |gemessener Wert – realer Wert| . Mit anderen Worten ist der absolute Fehler der absolute Wert der Differenz zwischen den gemessenen oder geschätzten Werten und den tatsächlichen Werten.
In mathematischer Sprache ausgedrückt bleibt es wie folgt:
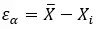
Es ist erwähnenswert, dass es sich um eine grundlegende Messung in vielen Bereichen wie Wissenschaft, Technologie, Ingenieurwesen und Wirtschaft handelt, da es die Bewertung der Genauigkeit der Ergebnisse und der Qualität von Modellen und Schätzungen ermöglicht.
Wie wird der absolute Fehler berechnet?
Die Berechnung des absoluten Fehlers ist einfach:
Der gemessene oder geschätzte Wert wird vom tatsächlichen Wert subtrahiert und der Absolutwert des Ergebnisses gebildet.
Wenn der tatsächliche Wert beispielsweise 10 beträgt und der gemessene oder geschätzte Wert 9 beträgt, wäre der absolute Fehler:
|9 – 10| = |-1| = 1.
Ein weiteres Beispiel: Wenn der tatsächliche Wert 15 und der gemessene oder geschätzte Wert 17 beträgt, wäre der absolute Fehler:
|17 – 15| = |2| = 2.
Sie können auch den mittleren absoluten Fehler berechnen, bei dem es sich um die Gesamtsumme der absoluten Fehler dividiert durch die Anzahl der Messungen oder Schätzungen handelt. Um es zu berechnen, müssen Sie der folgenden Formel folgen:
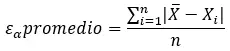
Dies ist nützlich, wenn Sie viele Messungen oder Schätzungen haben und sich einen allgemeinen Überblick über die Genauigkeit der Ergebnisse verschaffen möchten.
Angenommen, wir haben die folgenden Messungen oder Schätzungen:
Aktueller Wert: 20
Messwert 1:18
Messwert 2:22
Messwert 3:19
Wir berechnen den absoluten Fehler für jede Messung wie folgt:
Absoluter Fehler 1: |18 – 20| = 2
Absoluter Fehler 2: |22 – 20| = 2
Absoluter Fehler 3: |19 – 20| = 1
Wir berechnen den durchschnittlichen absoluten Fehler wie folgt: (2 + 2 + 1) ÷ 3 = 1,67. Dies bedeutet, dass Messungen oder Schätzungen im Durchschnitt innerhalb von 1,67 Einheiten vom wahren Wert abweichen.
Was ist der relative Fehler?
Der relative Fehler ist ein Maß für die Genauigkeit einer Messung oder Schätzung im Verhältnis des absoluten Fehlers zum wahren Wert.
Er wird durch die Formel dargestellt: (absoluter Fehler) ÷ (realer Wert) . In mathematischer Sprache ausgedrückt bleibt es wie folgt:
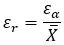
Der relative Fehler ist nützlich, um die Präzision verschiedener Messungen oder Schätzungen zu vergleichen, insbesondere wenn die tatsächlichen Werte unterschiedlich sind.
Wie wird der relative Fehler berechnet?
Bei der Berechnung des relativen Fehlers wird der absolute Fehler normiert , sodass die Genauigkeit verschiedener Messungen oder Schätzungen unabhängig von ihren tatsächlichen Werten verglichen werden kann.
Angenommen, Sie haben zwei Messungen oder Schätzungen, A und B, mit wahren Werten von 10 bzw. 100 und absoluten Fehlern von 1 bzw. 5.
Der relative Fehler für Messung A wäre (1) ÷ (10) = (0,1), während der relative Fehler für Messung B (5) ÷ (100) = (0,05) wäre. Dies weist darauf hin, dass Messung B relativ gesehen genauer ist als Messung A, obwohl sie einen größeren absoluten Fehler aufweist.
Hier sind einige Beispiele, wie der relative Fehler berechnet werden kann:
1. Messen Sie die Höhe eines Gebäudes und sie wird auf 100 Meter geschätzt:
Nach der Messung stellen wir fest, dass es tatsächlich 98 Meter lang ist.
Der absolute Fehler wäre 2 Meter und der relative Fehler wäre (2) ÷ (98) = 0,0204 oder 2,04 %.
2. Angenommen, Sie möchten das Gewicht eines Gegenstands messen und schätzen, dass dieser 10 Kilogramm wiegt.
Nach der Messung stellten wir fest, dass es tatsächlich 9,5 Kilogramm wiegt.
Der absolute Fehler wäre 0,5 Kilogramm und der relative Fehler wäre (0,5) ÷ (9,5) = 0,0526 oder 5,26 %.
3. Angenommen, Sie möchten die Länge eines Bretts messen und diese wird auf 200 Zentimeter geschätzt.
Nach der Messung stellen wir fest, dass es tatsächlich 201 Zentimeter sind.
Der absolute Fehler wäre 1 Zentimeter und der relative Fehler wäre (1) ÷ (201) = 0,00498 oder 0,498 %.
In jedem dieser Beispiele stellt der relative Fehler ein Maß für die Präzision der Messung dar, ausgedrückt als Verhältnis des absoluten Fehlers zum wahren Wert. Dadurch können Sie die Genauigkeit verschiedener Messungen und Schätzungen vergleichen, unabhängig von ihren tatsächlichen Werten.
Was ist der Unterschied zwischen absolutem Fehler und relativem Fehler?
Absoluter Fehler und relativer Fehler sind zwei unterschiedliche Maße zur Bewertung der Genauigkeit eines Ergebnisses oder Modells.
Der absolute Fehler bezieht sich auf die Differenz zwischen dem tatsächlichen oder wahren Wert einer Größe und dem geschätzten oder gemessenen Wert. Er kann als Differenz zwischen dem tatsächlichen Wert und dem geschätzten Wert berechnet werden:
Absoluter Fehler = tatsächlicher Wert – geschätzter Wert
Der absolute Fehler kann positiv oder negativ sein, je nachdem, ob der geschätzte Wert größer oder kleiner als der wahre Wert ist.
Andererseits bezieht sich der relative Fehler auf die Beziehung zwischen dem absoluten Fehler und dem realen oder wahren Wert . Er kann als Bruchteil des absoluten Fehlers und des wahren Werts berechnet werden:
Relativer Fehler = absoluter Fehler ÷ tatsächlicher Wert
Der relative Fehler wird üblicherweise als Prozentsatz ausgedrückt . Diese Art von Fehler ermöglicht es, die Genauigkeit verschiedener Ergebnisse oder Modelle unabhängig von ihrer Größe zu vergleichen.
Beispielsweise kann ein absoluter Fehler von 1,0 eine signifikante Abweichung von einem kleinen Betrag, aber nicht von einem großen Betrag sein. Der relative Fehler ist jedoch in beiden Fällen derselbe.
Kurz gesagt misst der absolute Fehler die Differenz zwischen dem tatsächlichen Wert und dem geschätzten Wert, während der relative Fehler die Genauigkeit der Schätzung im Hinblick auf ihre Beziehung zum tatsächlichen Wert misst.
Welche Anwendungen gibt es für den absoluten Fehler und den relativen Fehler?
Absolute Fehler und relative Fehler haben ein breites Anwendungsspektrum in verschiedenen Bereichen, darunter:
- Wissenschaft – In wissenschaftlichen Experimenten zur Bewertung der Genauigkeit von Messungen und der Qualität der Ergebnisse.
- Technologie – Herstellung und Qualitätskontrolle zur Bewertung der Genauigkeit von Maschinen und Geräten.
- Engineering – Konstruktion und Design zur Bewertung der Messgenauigkeit und zur Sicherstellung der Qualität der Endprodukte.
- Wirtschaftswissenschaften : Vermögensbewertung und finanzielle Risikoabschätzung, um die Genauigkeit von Prognosen zu beurteilen und fundierte Entscheidungen zu treffen.
- Mathematik und Statistik : Modellierung und Schätzung zur Beurteilung der Genauigkeit von Ergebnissen und zur Verbesserung von Modellen.
Beispiele zur Berechnung des absoluten Fehlers und des relativen Fehlers
Hier sind zwei einfache Beispiele zur Berechnung sowohl des absoluten als auch des relativen Fehlers:
1. Angenommen, das Gewicht eines Objekts wird auf 3,0 kg geschätzt und sein tatsächliches Gewicht beträgt 2,8 kg.
Den absoluten Fehler berechnen wir wie folgt:
Absoluter Fehler = tatsächlicher Wert – geschätzter Wert = 2,8 kg – 3,0 kg = -0,2 kg
Den relativen Fehler berechnen wir wie folgt:
Relativer Fehler = Absoluter Fehler ÷ Tatsächlicher Wert = -0,2 kg ÷ 2,8 kg = -0,0714 oder -7,14 %
2. Angenommen, das Volumen eines Behälters wird auf 50 Liter geschätzt und sein tatsächliches Volumen beträgt 45 Liter.
Den absoluten Fehler berechnen wir wie folgt:
Absoluter Fehler = tatsächlicher Wert – geschätzter Wert = 45 Liter – 50 Liter = -5 Liter
Den relativen Fehler berechnen wir wie folgt:
Relativer Fehler = Absoluter Fehler ÷ Tatsächlicher Wert = -5 Liter ÷ 45 Liter = -0,1111 oder -11,11 %
3. Angenommen, die Bevölkerung einer Stadt wird auf 1 Million Menschen geschätzt und die tatsächliche Zahl beträgt 975.000 Menschen.
Den absoluten Fehler berechnen wir wie folgt:
Absoluter Fehler = tatsächlicher Wert – geschätzter Wert = 975.000 – 1.000.000 = -25.000
Den relativen Fehler berechnen wir wie folgt:
Relativer Fehler = Absoluter Fehler ÷ Tatsächlicher Wert = -25.000 ÷ 975.000 = -0,0257 oder -2,57 %
4. Angenommen, die Fläche eines Fußballfeldes wird auf 10.000 Quadratmeter geschätzt und die tatsächliche Fläche beträgt 9.900 Quadratmeter.
Den absoluten Fehler berechnen wir wie folgt:
Absoluter Fehler = tatsächlicher Wert – geschätzter Wert = 9.900 – 10.000 = -100 Quadratmeter
Den relativen Fehler berechnen wir wie folgt:
Relativer Fehler = Absoluter Fehler ÷ Tatsächlicher Wert = -100 ÷ 9900 = -0,0101 oder -1,01 %
In diesen Beispielen geben der absolute Fehler und der relative Fehler Aufschluss über die Genauigkeit der Schätzung. Der absolute Fehler sagt uns, wie stark die Schätzung vom wahren Wert abweicht, während der relative Fehler uns sagt, wie stark die Schätzung im Hinblick auf ihr Verhältnis zum wahren Wert abgewichen ist.