Was ist eulers zahl?

Die Eulersche Zahl (auch Eulersche Konstante genannt) ist eine wichtige und wesentliche mathematische Zahl in verschiedenen Bereichen der Mathematik, einschließlich Zahlentheorie, Topologie, Gruppentheorie und Funktionentheorie. Es wird durch den griechischen Buchstaben „e“ dargestellt und sein ungefährer Wert beträgt 2,71828.

Die Zahl e ergibt sich aus der Formel für die Exponentialfunktion und ist eine Grundzahl der komplexen Zahlentheorie.

Es ist auch eine natürliche Zahl, die bei der Lösung vieler mathematischer Probleme auftaucht, einschließlich der Berechnung von Wahrscheinlichkeiten und der Modellierung von Wachstums- und Zerfallsprozessen.

Was ist der Ursprung der Eulerschen Zahl?

Die Euler-Zahl ist nach dem Schweizer Mathematiker Leonhard Euler (1707-1783) benannt, der einer der größten Mathematiker aller Zeiten war und als Vater der modernen Mathematik gilt.

Euler leistete wertvolle Beiträge zu vielen Bereichen der Mathematik, darunter Zahlentheorie, Geometrie, Analysis, Physik und Astronomie.

Er war es, der in seiner Arbeit über die Berechnung und Theorie der Logarithmen erstmals die Zahl e (sogenannte Eulersche Zahl) definierte und verwendete. Eulers Formel für komplexe Zahlen ist auch einer seiner bemerkenswertesten Beiträge zur Mathematik.

Wie wird dieser Wert ermittelt?

Tatsächlich gibt es mehrere Methoden zur Berechnung der Euler-Zahl. Es ist jedoch erwähnenswert, dass keine der beiden Methoden ein genaues Ergebnis liefert. Daher ist seine Nummerierung fortlaufend und unendlich, wird jedoch nicht wiederholt.

Tatsächlich sind derzeit mehr als 1 Billion Zahlen bekannt, aus denen sich die Zahl e zusammensetzt. Die unendliche Reihe, die die Euler-Zahl definiert, ist:

Gold „!“ ist eine Fakultät, die als Produkt aller natürlichen Zahlen bis zu dieser Zahl definiert ist. Zum Beispiel:

5! = 5 4 3 2 1 = 120

Wir können diese Reihe grafisch als Summe einer Reihe von Rechtecken mit der Höhe 1 und abnehmender Breite betrachten, wobei die Breite jedes Rechtecks 1/n! beträgt, wobei n die Anzahl der Fakultäten ist.

Wenn wir die Anzahl der Rechtecke in der Summe erhöhen, nähert sich die Fläche unter der Kurve der Exponentialfunktion immer mehr der Eulerschen Zahl an.

Zusammenfassend ist die Eulersche Zahl eine Zahl, die sich aus der Summe einer unendlichen Reihe ergibt und für viele Bereiche der Mathematik von grundlegender Bedeutung ist. Obwohl es sich um eine irrationale Zahl handelt, beträgt ihr ungefährer Wert 2,71828.

Es ist wichtig zu bedenken, dass Euler selbst diese Methode zur Berechnung von e auf 18 Dezimalstellen implementiert hat.

Eine andere Möglichkeit, es zu berechnen:

Wir können den ungefähren Wert der Euler-Zahl auf einer Geraden mithilfe einer Reihe endlicher Terme berechnen. Nehmen wir zum Beispiel die erste oben definierte unendliche Reihe:

Wir können den Näherungswert berechnen, indem wir die ersten Terme der Reihe addieren. Wenn wir zum Beispiel die ersten 6 Begriffe hinzufügen:

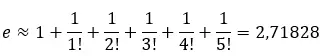
Wir können diese Reihe auf einer Linie darstellen, um zu sehen, wie sie sich dem ungefähren Wert 2,71828 nähert.

Grafisch kann die Linie, die die Euler-Zahl darstellt, als eine Reihe von Rechtecken mit der Höhe 1 und abnehmender Breite gezeichnet werden, wobei die Breite jedes Rechtecks 1/n! beträgt, wobei n die Anzahl der Fakultäten ist.

Wenn wir die Anzahl der Rechtecke in der Summe erhöhen, nähert sich die Fläche unter der Kurve der Exponentialfunktion immer mehr der Eulerschen Zahl an.

Exponentialgleichungen mit Euler-Zahl

Exponentialgleichungen mit der Euler-Zahl können zur Modellierung einer Vielzahl von Phänomenen in Naturwissenschaften wie Physik, Biologie, Wirtschaftswissenschaften und anderen verwendet werden. Hier sind einige Beispiele:

Exponentielles Wachstum und Verfall

Dieses Modell beschreibt die Geschwindigkeit, mit der eine Population wächst oder schrumpft , oder die Geschwindigkeit, mit der eine giftige Substanz abgebaut wird.

Wenn eine Bevölkerung beispielsweise um 5 % pro Jahr wächst, kann ihre Größe durch die Formel beschrieben werden:

P(t) = P0 · e ^0,05t , wobei P0 die anfängliche Populationsgröße ist.

Modelle des radioaktiven Zerfalls

Dieses Modell beschreibt die Geschwindigkeit, mit der radioaktive Atome im Laufe der Zeit zerfallen.

Die Formel lautet wie folgt:

N(t) = N0 e ^-λt

Dabei ist N0 die Anfangszahl der Atome, λ eine Konstante, die vom radioaktiven Material abhängt, und t die Zeit.

Dies sind nur einige Beispiele dafür, wie Exponentialgleichungen mit der Eulerschen Zahl in der Praxis angewendet werden können. Es gibt viele andere Bereiche, in denen Exponentialgleichungen nützlich und relevant sind.

Welche Anwendungen gibt es für die Eulersche Zahl?

Die Euler-Zahl hat ein breites Anwendungsspektrum in verschiedenen Bereichen der Mathematik und Naturwissenschaften. Einige der Felder, in denen die Zahl e verwendet wird, sind:

• Berechnung und mathematische Analyse : Wird bei der Untersuchung exponentieller und logarithmischer Funktionen sowie bei der Auflösung von Differentialgleichungen verwendet.
• Zahlentheorie – wird zur Untersuchung der Verteilung von Primzahlen und zur Lösung von Problemen im Zusammenhang mit der Zahlentheorie verwendet.
• Wahrscheinlichkeit und Statistik : Wird zur Lösung von Problemen im Zusammenhang mit der Wahrscheinlichkeitsverteilung und zur Schätzung erwarteter Werte verwendet.
• Kryptographie – Wird bei der Untersuchung von Verschlüsselungs- und Entschlüsselungsalgorithmen verwendet.
• Physik – wird zur Lösung von Problemen im Zusammenhang mit Thermodynamik, Quantenmechanik und statistischer Physik verwendet.
• Chemie : Wird zur Lösung von Problemen im Zusammenhang mit der chemischen Thermodynamik und chemischen Kinetik verwendet.

Eulers Formel für komplexe Zahlen

Eulers Formel für komplexe Zahlen stellt eine Beziehung zwischen trigonometrischen und exponentiellen Funktionen her. Die Formel lautet:

Dabei ist „e“ die Basis natürlicher Logarithmen, „i“ die imaginäre Einheit, „x“ eine reelle Zahl und „cos“ und „sin“ die trigonometrischen Funktionen Kosinus bzw. Sinus.

Diese Formel ist in vielen Bereichen der Mathematik sehr nützlich, einschließlich der Zahlentheorie, der Funktionentheorie und der Komplexitätstheorie, und hat eine Vielzahl von Anwendungen in den Ingenieurwissenschaften, der Physik und den Wirtschaftswissenschaften.

Ein praktisches Anwendungsbeispiel ist die Darstellung von Signalen und Systemen in der Fourier-Analyse, bei der periodische Signale als Summe komplexer Sinussignale dargestellt werden.

Die Eulersche Formel wird verwendet, um zu beschreiben, wie sich diese komplexen Signale auf die tatsächlichen trigonometrischen Funktionen beziehen, die die einzelnen Sinussignale beschreiben.

Eulersche Zahl und Zinseszins

Zinseszins ist ein Finanzkonzept , das den Prozess beschreibt, durch den ein Geldbetrag, der als Kapital bezeichnet wird, Zinsen auf Zinsen erhält, die im Laufe der Zeit steigen.

Mit anderen Worten: Der Zinsertrag einer Investition stammt nicht nur aus dem Anfangskapital, sondern auch aus den in früheren Perioden erwirtschafteten Zinsen.

Die Euler-Zahl und der Zinseszins hängen zusammen, da die Formel zur Berechnung des Zinseszinses die Euler-Zahl verwendet. Die Formel für den Zinseszins lautet:

A = P e ^rt

Dabei ist A der Endbetrag, P der Kapitalbetrag, r der Zinssatz, t die Zeit und e die Euler-Zahl. Auf diese Weise ist die Euler-Zahl ein wichtiger Faktor in der mathematischen Formulierung zur Berechnung des Zinseszinses.

Ein Beispiel für die Berechnung des Zinseszinses mit konkreten Zahlen wäre:

Angenommen, wir haben eine Anlage von 1.000 € zu einem Zinssatz von 5 % pro Jahr für 2 Jahre. Die Formel zur Berechnung des Zinseszinses wäre:

A = P e ^rt = 1000 e ^{0,05 2} = 1000 1,1025 = 1102,5 €.

Das bedeutet, dass sich unser Anfangskapital von 1.000 € durch den erwirtschafteten Zinseszins nach 2 Jahren auf 1.102,5 € erhöht hat.

Beispiele für mathematische Übungen mit der Euler-Zahl

Hier sind zwei Beispiele gelöster mathematischer Probleme mit der Euler-Zahl:

1. Finden Sie den Wert von „e ^ix “, wobei x eine reelle Zahl ist:

Eulers Identität sagt uns, dass e ^ix = cos(x) + i · sin(x). Wenn wir also den Wert von x kennen, können wir den Wert von e ^ix mithilfe trigonometrischer Funktionen berechnen.

2. Berechnen Sie e^(x ² ) für einen gegebenen Wert von x:

Wir können die Taylor-Reihe verwenden, um den Wert von e^(x ² ) zu berechnen. Die Taylor-Reihe von e ^x ist eine unendliche Entwicklung, die es ermöglicht, abhängig vom verwendeten Term sukzessive Näherungen an den Wert von e ^x zu berechnen.

Wenn wir x in dieser Reihe durch x ² ersetzen, erhalten wir die Taylor-Reihe für e^(x ² ).