Komplexe Zahlen sind eine Menge bestehend aus reellen Zahlen und imaginären Zahlen . Diese letzten beiden Zahlensätze können grafisch mithilfe der realen Linie und der imaginären Linie dargestellt werden . Und wenn wir beide Geraden in die gleiche Ebene legen, entsteht die bekannte komplexe Ebene.
Was ist der komplexe Plan?
Die komplexe Ebene wird durch die reale Achse (X-Achse), die der realen Linie entspricht, und andererseits die imaginäre Achse (Y-Achse), die die imaginäre Linie konzeptualisiert, gebildet.
Es ist zu beachten, dass dieser Plan alle komplexen Zahlen umfasst. Unabhängig davon, wie klein oder klein sie ist oder in welcher Form eine komplexe Zahl geschrieben ist, kann sie daher grafisch auf dem Plan dargestellt werden. Sehen wir uns also an, wie diese Zahlen in der komplexen Ebene dargestellt werden.
Wie zeichnet man komplexe Zahlen auf der komplexen Ebene grafisch auf?
Wie wir bereits wissen (oder wenn Sie es nicht wissen, empfehlen wir Ihnen, unseren Artikel über komplexe Zahlen zu lesen), gibt es drei Möglichkeiten , einen Komplex zu schreiben: die Binomialform, die Polarform und die trigonometrische Form. Jeder drückt den komplexen Wert gemäß einer anderen Struktur aus, daher ist die Methode zur Erstellung der grafischen Darstellungen unterschiedlich.
Als nächstes erklären wir die Vorgehensweise in den drei Fällen:
Darstellung in Binomialform
Wenn wir eine komplexe Zahl in Binomialschreibweise haben, was am häufigsten vorkommt, müssen wir uns die Struktur der Zahl ansehen:

Dabei ist a der Realteil und b der Imaginärteil.
Aus diesem Wissen schließen wir, dass der Wert von a derjenige ist, den wir für die Abszisse (reale Achse) verwenden, und der Wert von b derjenige, den wir für den Computer (imaginäre Achse) verwenden. Anhand des folgenden Beispiels werden Sie es besser verstehen.
Wir werden versuchen, die Zahl darzustellen: 3 + 2i.
Als erstes muss das Diagramm gezeichnet werden (wobei zu beachten ist, dass die horizontale Achse die reale Achse und die vertikale Achse die imaginäre Achse ist):

Dann lokalisieren wir den Punkt des Graphen in kartesischen Koordinaten (x, y), die wir aus der komplexen Zahl ableiten. In diesem praktischen Beispiel ist unser Punkt (3, 2).
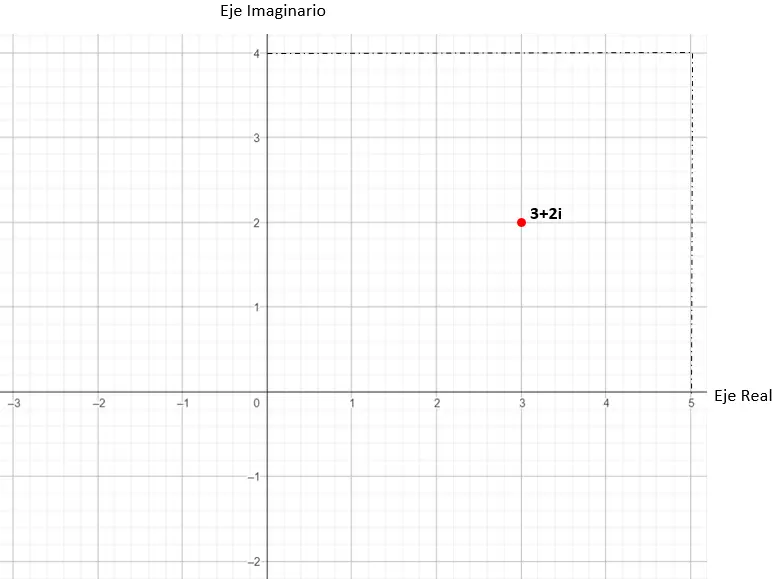
Somit würde der Wert 3 + 2i in der komplexen Ebene dargestellt.
Darstellung in Polarform
Wir werden nun sehen, wie eine komplexe Zahl in Polarform dargestellt wird. Um diese Methode vollständig zu verstehen, müssen Sie wissen, dass die Polarschreibweise eine komplexe Zahl basierend auf dem Modul und dem Argument definiert. Die in der grafischen Darstellung als Polarkoordinaten (und nicht als kartesische Koordinaten!) verwendet werden.
Und das Hauptmerkmal des Polarkoordinatensystems besteht darin, dass die Position eines Punktes durch einen Vektor und einen Winkel beschrieben wird (im Gegensatz zur vorherigen Methode). Was dem Modul und dem Argument komplexer Zahlen entspricht. Als nächstes zeigen wir Ihnen die universelle Formel für die Polarform einer komplexen Zahl:

Wobei |z| ist der Modul und α ist das Argument. Diese beiden Variablen werden im Plan übersetzt durch:
- Modul: Es ist die Länge, die einen Vektor definiert (zwischen dem Ursprung und dem Punkt, der unserer Zahl entspricht).
- Argument: ist der Winkel, den der Vektor mit der X-Achse bildet.
Daher entspricht der Modul einer komplexen Zahl der Länge des Vektors, den wir zur Erstellung des Diagramms verwenden. Während das Argument oder der Winkel der komplexen Zahl der Winkel zwischen dem Vektor und der X-Achse ist. Unten sehen Sie ein Diagramm, in dem alle Variablen platziert sind :
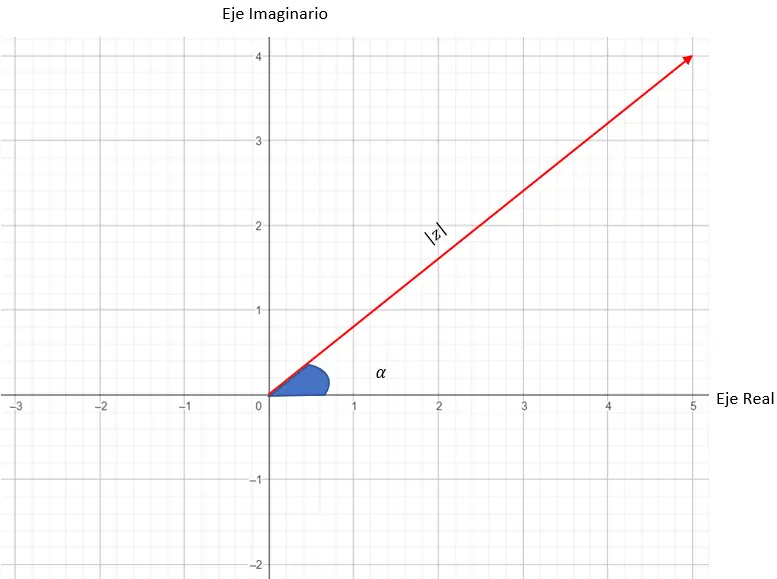
Jetzt werden wir versuchen, die Zahl darzustellen: 3 45 .
Zuerst müssen wir das Modul und das Argument identifizieren:
- Modul: 3.
- Argument: 45 Grad.
Als nächstes müssen wir die Punkte im Diagramm finden, die einen Modul von 3 haben. In diesem Fall funktioniert jeder Punkt auf einem Kreis mit Radius 3.
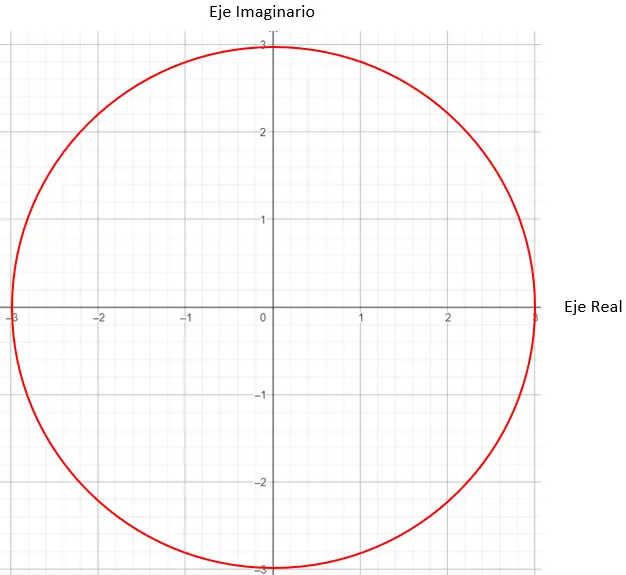
Und um den genauen Punkt zu bestimmen, müssen wir die Bedingung stellen, dass der vom Modul erzeugte Vektor und der Ursprung einen Winkel von 45 Grad mit der X-Achse bilden müssen.
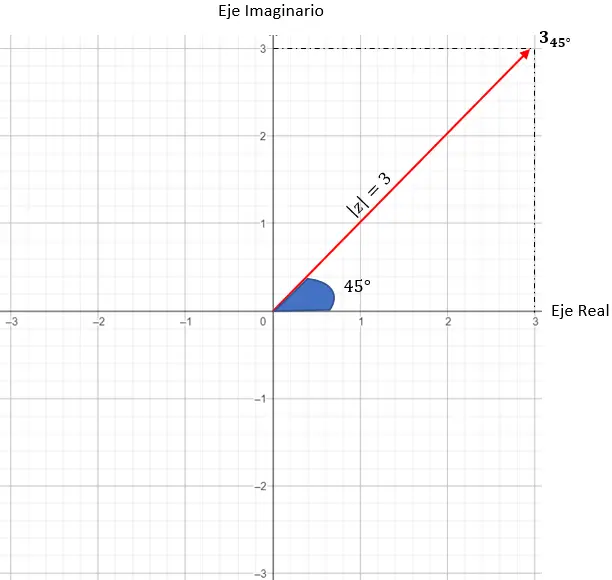
Und wir haben bereits eine komplexe Zahl in Polarschreibweise dargestellt.
Darstellung in trigonometrischer Form
Abschließend müssen wir noch erklären, wie eine komplexe Zahl in trigonometrischer Form dargestellt wird. Dieser und der vorherige Fall sind praktisch identisch, da die Polarform und die trigonometrische Form dieselben Daten verwenden, um eine komplexe Zahl auszudrücken: den Modul und das Argument. Dadurch ändert sich lediglich die Struktur des Ausdrucks:

Wo, |z| ist der Modul und α ist das Argument.
Wir müssen daher die gleiche Methode wie im vorherigen Fall nutzen: Verwenden Sie den Modul als „Länge“ und das Argument als Winkel. Wenn Sie sich das folgende Beispiel ansehen, werden Sie es besser verstehen.
Wir stellen z = 4 · (cos (45) + i · sin(45)) dar.
Als erstes müssen Sie das Modul und den Winkel identifizieren:
- Modul: 4.
- Argument: 45 Grad.
Als nächstes müssen wir die Punkte im Diagramm finden, die einen Modul von 4 haben. In diesem Fall funktioniert jeder Punkt auf einem Kreis mit dem Radius 4.
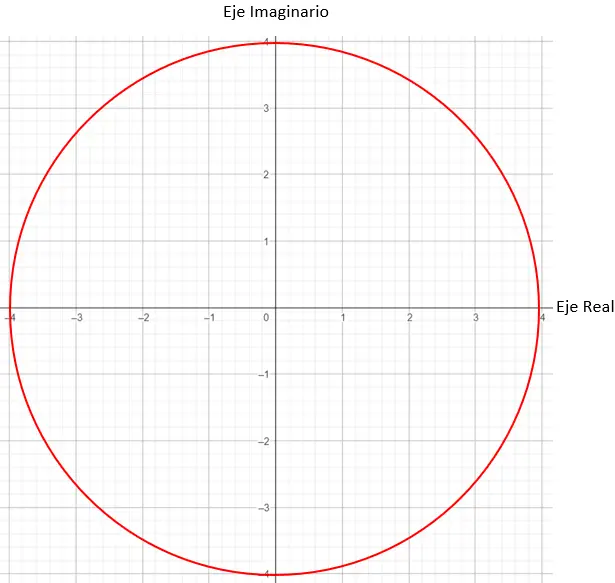
Und schließlich lokalisieren wir den genauen Punkt, wobei der Winkel zwischen dem Modulvektor und der X-Achse 45 Grad betragen muss, wie das Argument sagt.
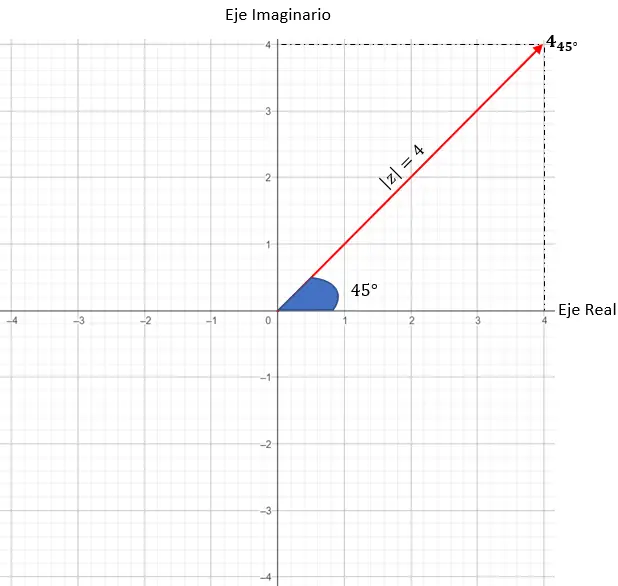
Und so stellen wir eine komplexe Zahl in trigonometrischer Form dar.
Komplexe Flugzeugübung
Zum Abschluss dieser Veröffentlichung bieten wir noch eine letzte Übung an. Wir empfehlen Ihnen dringend, das Problem zu lösen, da Sie auf diese Weise das in diesem Artikel erläuterte Wissen festigen.
Beweis der grafischen Darstellung der folgenden drei komplexen Zahlen auf der komplexen Ebene:
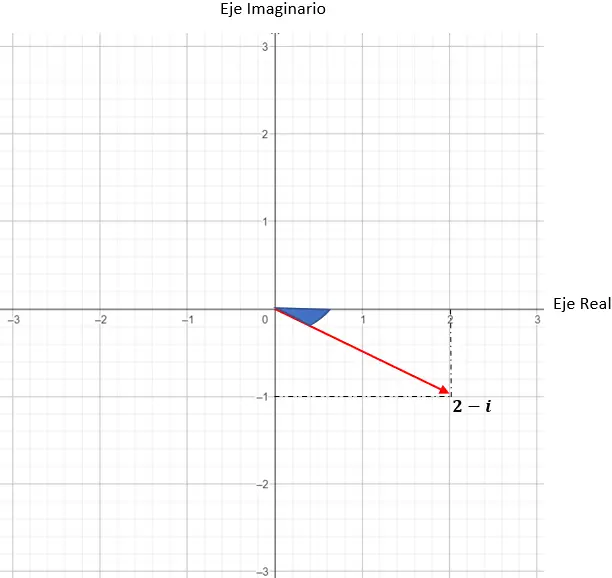
z = 2 – ich
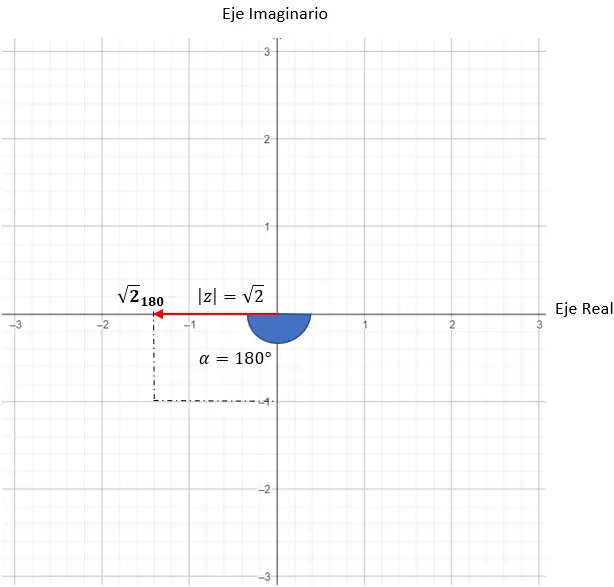
w = √2180
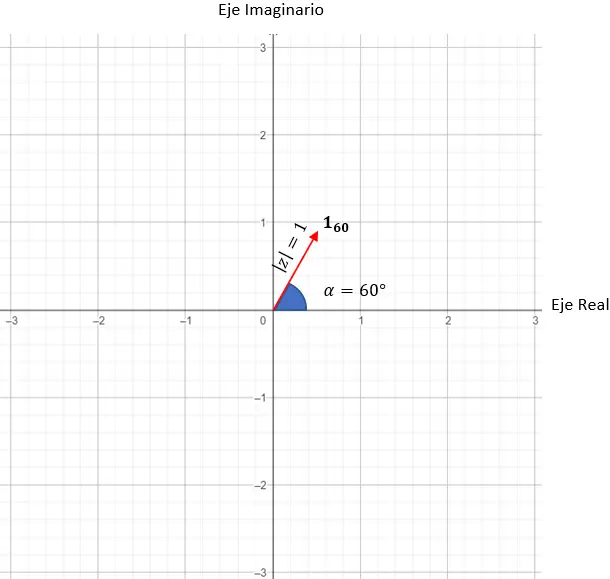
p = cos(60) + I sin(60)