Die Eulersche Formel ist ein mathematisches Konzept, das zwei elementare Konzepte der Mathematik verbindet: komplexe Zahlen und Trigonometrie. Dies macht es zu einer der wichtigsten Konzeptualisierungen und mit den meisten Anwendungen in der gesamten Mathematik. In diesem Artikel werden wir sehen, wie diese Formel aussieht und welche Verwendungsmöglichkeiten sie hat.
Wie lautet Eulers Formel?
Die Euler-Formel ist eine grundlegende mathematische Gleichung, die auf der Euler-Zahl basiert und komplexe Zahlen mit der Trigonometrie in Beziehung setzt. Es wurde im 18. Jahrhundert vom Schweizer Mathematiker Leonhard Euler entdeckt und seitdem in verschiedenen Bereichen eingesetzt, von der Physik bis zur Informatik.
Eulers Formel wird als e ix = cos(x) + i sin(x) geschrieben, wobei e die Basis des natürlichen Logarithmus, i die imaginäre Einheit (definiert als Quadratwurzel von -1) und x ein reeller Wert ist Nummer. Diese Gleichung gibt an, dass die komplexe Zahl e ix gleich der Summe der reellen Zahl cos(x) und dem Produkt der imaginären Zahl i mit der reellen Zahl sin(x) ist.

Die Bedeutung der Euler-Formel liegt darin, dass sie es ermöglicht, komplexe Zahlen durch reelle Zahlen und Trigonometrie auszudrücken, wodurch sie einfacher zu manipulieren und zu berechnen sind.
Beweis der Eulerschen Formel
Der Beweis der Eulerschen Formel basiert auf der Verwendung der Taylor-Reihe für die Exponentialfunktion und der trigonometrischen Identität für Kosinus und Sinus.
Zunächst betrachten wir die Taylor-Reihe für die Exponentialfunktion:

Als nächstes ersetzen wir x durch ix in der obigen Gleichung, wobei i die imaginäre Einheit ist (Quadratwurzel von -1):
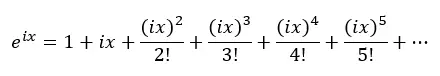
Also wenden wir die Potenzen von i an und setzen sie in die vorherige Gleichung ein:
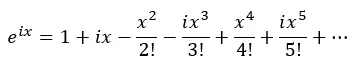
Nun gruppieren wir die realen Terme und die Terme mit i:
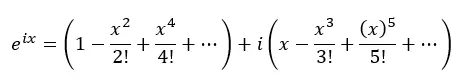
Tatsächlich ist jede der Klammern oben die Taylor-Reihe für Kosinus und Sinus:
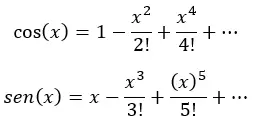
Schließlich vereinfachen wir (indem wir jeden Ausdruck in Klammern durch Kosinus und Sinus von x ersetzen) und erhalten:

Beispiel für Eulers Formel
Nachdem Sie nun wissen, wie diese mathematische Formel funktioniert, empfehlen wir Ihnen, das folgende praktische Beispiel zu lösen: Drücken Sie die komplexe Zahl e 2i (im Bogenmaß) in Binomialform aus:
Die Hauptanwendung der Euler-Formel besteht darin, eine in Exponentialform ausgedrückte komplexe Zahl in Binomialform umzuwandeln. Wir verwenden daher die Formel : e ix = cos(x) + i sin(x)
e 2i = cos(2) + i sin(2)
e2i = -0,416 + 0,909i
Und wir hätten die Zahl bereits in Binomialform. Von dort aus können wir die grafische Darstellung in der komplexen Ebene erstellen. Dazu muss man verstehen, dass eine komplexe Zahl in der komplexen Ebene dargestellt wird, wobei als Koordinaten der Realteil auf der Abszisse (x-Achse) und der Imaginärteil auf der Ordinate (y-Achse) verwendet werden.
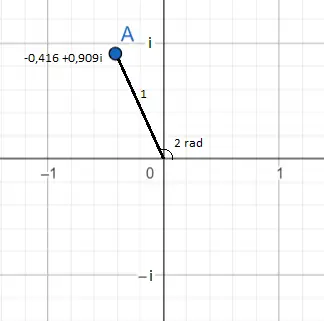
Im vorherigen Bild ist die komplexe Zahl e 2i dargestellt, die -0,416 + 0,909i entspricht. Dies ist als blauer Punkt zu erkennen. Seine Lage im Flugzeug kann aus zwei Blickwinkeln gesehen werden.
Das erste und offensichtlichste ist die Darstellung der Zahl in Binomialform : -0,416 (auf der Abszisse) und 0,909 (auf dem Computer). Und das zweite ist in Exponentialform : Der Modul von e 2i ist gleich 1, weil es die Zahl ist, die vor e steht (da es keine Zahl vor e gibt, müssen wir uns vorstellen, dass es eine 1 gibt) und im Exponenten gibt es eine 2, daher entspricht das Argument oder der Winkel zwei Bogenmaßen.
Wenn Sie diesen letzten Absatz nicht ganz verstehen , empfehlen wir Ihnen, unseren Artikel über komplexe Zahlen zu lesen. Nun, hier erklären wir sehr ausführlich die verschiedenen Arten, eine komplexe Zahl und alle ihre Eigenschaften zu schreiben.
Grafische Darstellung der Eulerschen Formel
Im vorherigen Beispiel konnten Sie sehen, wie die Eulersche Formel angewendet und in der komplexen Ebene grafisch dargestellt wird. Wenn wir jedoch etwas weiter gehen und versuchen, eine Funktion darzustellen, die der Eulerschen Formel entspricht, finden wir etwas sehr Merkwürdiges: Sie erzeugt einen Kreis mit dem Radius 1 :
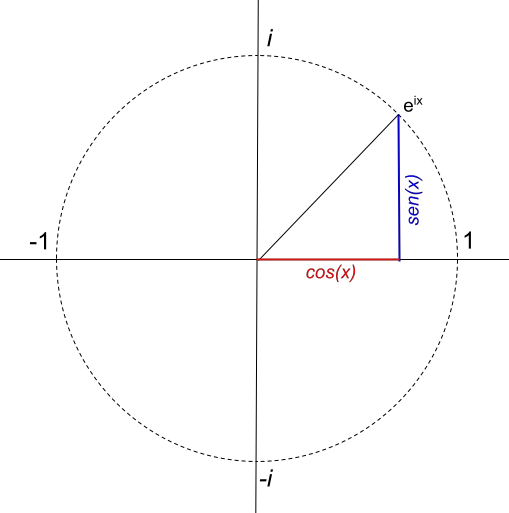
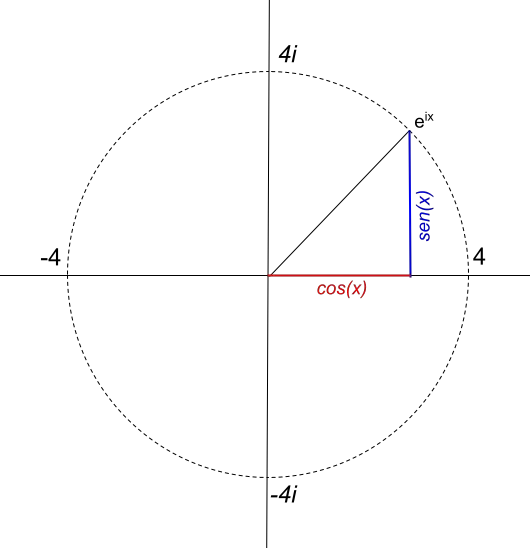
Der Radius des Kreises hängt jedoch direkt vom Wert des Moduls der komplexen Zahl ab. Wenn wir beispielsweise einen Kreis mit dem Radius 4 darstellen möchten, lautet die Funktion 4e ix . Die Funktion 4e ix wird also wie folgt dargestellt:
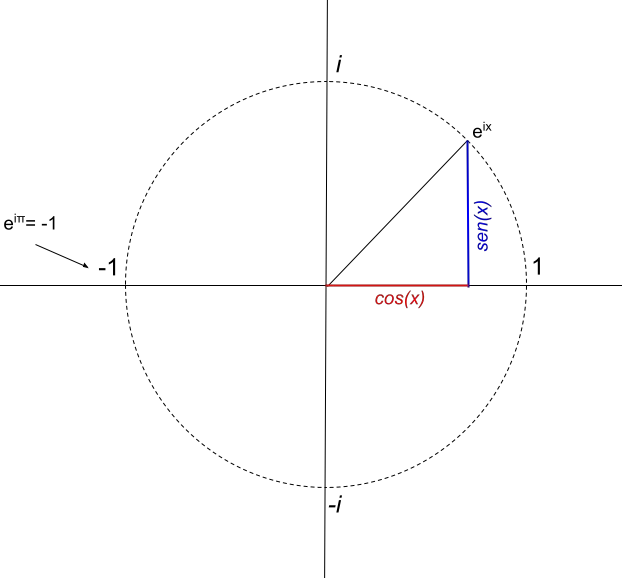
Zurück zum Kreis mit Radius 1: Wenn wir uns entscheiden, e iπ (im Bogenmaß) darzustellen, müssen wir zunächst Folgendes berechnen:
e πi = cos(π) + i sin(π)
eπi = -1 + i 0
eπi = -1
Wir erhalten e πi = -1, was die berühmte Euler-Identität ist.
Daraus schließen wir, dass die komplexe Zahl e πi nur einen Realteil hat, der gleich -1 ist. Daher wäre seine Darstellung so:
Anwendungen der Eulerschen Formel
- Komplexe Zahlen: Die Eulersche Formel ist eine Beziehung zwischen trigonometrischen Funktionen und komplexen Zahlen. Mit dieser Formel können wir komplexe Zahlen auf verschiedene Arten ausdrücken: binomial, exponentiell und polar.
- Taylor-Reihe: Die Euler-Formel wird zur Erweiterung von Taylor-Reihenfunktionen verwendet.
- Lineare Algebra: Die Eulersche Formel wird bei der Matrixdiagonalisierung verwendet, einer grundlegenden Technik der linearen Algebra.
- Differential- und Integralrechnung: Die Eulersche Formel wird bei der Lösung von Differentialgleichungen verwendet, einer relevanten Technik in der Analysis.
Darüber hinaus findet es Anwendung in vielen mathematischen Theorien und sogar in Konzepten außerhalb des mathematischen Bereichs, beispielsweise in physikalischen Theoremen.
Schlussfolgerungen
Wie Sie in diesem Artikel gesehen haben, findet die Eulersche Formel ihre größte Anwendung bei komplexen Zahlen : in ihrem numerischen Ausdruck und in ihrer Darstellung. Es stimmt, dass dies in der Algebra einige Anwendung findet, aber im Wesentlichen arbeiten Sie mit komplexen Zahlen. Deshalb ist es vor allem wichtig, sie gut zu verstehen.
Dennoch hoffen wir, dass wir Ihnen dabei geholfen haben, dieses Konzept besser zu verstehen. Und wenn Sie Fragen haben oder nicht wissen, wie man eine Übung durchführt, schreiben Sie uns gerne in die Kommentare.