Einfache Zinsen sind die gebräuchlichste Methode zur Zinsberechnung und werden für verschiedene Zwecke verwendet, vom Kauf eines Eigenheims bis zur Aufnahme eines Privatkredits. Wenn Sie einmal einfache Zinsen berechnen müssen, zeigt Ihnen diese Anleitung Schritt für Schritt, wie das geht. Um Ihnen die Arbeit zu erleichtern, stellen wir Ihnen auch einen Online-Rechner zur Verfügung.
Einfacher Zinsrechner
Dieser Online-Rechner für einfache Zinsen ist ein Tool, mit dem Sie alle Variablen berechnen können, die bei der Berechnung einfacher Zinsen eine Rolle spielen. Um es zu verwenden, wählen Sie einfach aus, was Sie berechnen möchten , und geben Sie die Daten für die abgefragten Variablen ein. Dann müssen Sie auf die Schaltfläche „Berechnen“ klicken und fertig.
Was ist einfacher Zins?
Der einfache Zinssatz ist der Zinssatz, der berechnet wird, wenn Sie einen Betrag für einen bestimmten Zeitraum anlegen oder verleihen . Er wird berechnet, indem der Anfangsbetrag mit dem Zinssatz und der Zeit multipliziert wird. Zusammenfassend lässt sich sagen, dass diese Zinsen für ständige und in der Regel kurzfristige finanzielle Maßnahmen verwendet werden.
Da Zinssatz und Laufzeit konstant gehalten werden, sind die Zinsen, die monatlich oder jährlich gezahlt werden müssen, immer gleich , da sich die Zinsen nicht erhöhen. Dies ist der Hauptunterschied zwischen einfachem Zins und Zinseszins .
Im folgenden Bild sehen Sie die Funktion, die den einfachen Zins darstellt, in Grün und die Zinseszinsfunktion, dargestellt in Blau. Wie wir auf dem Bild sehen können, hat es eine viel exponentiellere Form.
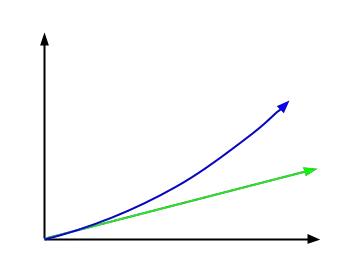
Formel zur Berechnung einfacher Zinsen
Die Formel zur Berechnung des einfachen Zinses lautet: I = C xixt , wobei folgende Variablen eingreifen:
- Anfangskapital (C): angelegter oder geliehener Geldbetrag, auf den einfache Zinsen berechnet werden.
- Zinssatz (i): Dieser Indikator gibt uns als Prozentsatz die Höhe der Zinsen im Verhältnis zur Zeit an. Es ist wichtig, es in der Formel so viel wie eins anzugeben (den Prozentwert durch einhundert dividieren).
- Zeit (t): Die Länge des Anlagezeitraums, im Allgemeinen ausgedrückt in Jahren. Im Folgenden zeigen wir Ihnen jedoch, wie Sie die Zeiteinheit in andere Zeiteinheiten umrechnen, z. B. Monate und Tage.
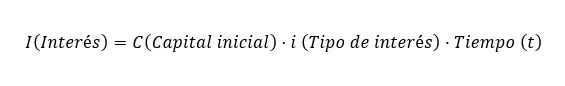
Um zu sehen, wie diese Formel verwendet wird, können wir das folgende Beispiel betrachten: Wir haben 1000 € mit einem jährlichen Zinssatz von 4 % investiert. Wie viel Zinsen werden wir nach drei Jahren generiert haben? Um die generierten Zinsen zu ermitteln, müssen wir die Formel anwenden: I = C x (i ÷ 100) xt = 1000 x (4 ÷ 100) x 3 = 120 €.
Anschließend können wir aus der Hauptformel die verschiedenen Variablen isolieren und so die Formeln erhalten, mit denen wir das Anfangskapital, den Zinssatz, die Zeit und das Endkapital berechnen können. Und genau das werden wir in den folgenden Abschnitten sehen, in denen wir Ihnen beibringen, wie Sie diese Variablen anhand der Formel berechnen, die Sie bereits gesehen haben, und einer weiteren sehr einfachen Formel.
Wie wird das Endkapital berechnet?
Um das Endkapital zu berechnen, wenden Sie einfach Logik an. Da der Endbetrag dann dem Anfangsbetrag entspricht, lautet die Formel nach Anwendung der Zinsen: Endkapital (Cf) = Anfangskapital (C) + Zinsen (I). Dieser Ausdruck ist die zweitwichtigste einfache Zinsformel, die wichtigste ist die vorherige.
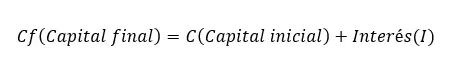
Nachdem Sie nun die Formel kennen, versuchen Sie, dieses praktische Beispiel zu lösen: Wie hoch ist das Endkapital, das Sie erhalten, wenn Sie 50.000 € über 4 Jahre investieren und einen Zinssatz von 20.000 € haben? Wir wenden einfach den Ausdruck von zuvor an: Endkapital (Cf) = Anfangskapital (C) + Zinsen (I) = 50.000 + 20.000 = 70.000 €.
Wie wird das Anfangskapital berechnet?
Wenn wir das Anfangskapital berechnen möchten, können wir je nach den Daten, die sie uns liefern, zwei Formeln verwenden. Erstens können wir den Ausdruck aus dem vorherigen Abschnitt anwenden, wenn wir das Endkapital und den durch die Zinsen generierten Betrag haben: Anfangskapital (C) = Endkapital (Cf) – Zinsen (I).
Zweitens können wir den Wert des Anfangskapitals in der einfachen Zinsformel (die wir am Anfang besprochen haben) isolieren. Übrig bliebe also Anfangskapital (C) = Zinsen (I) ÷ (Zeit (t) x Zinssatz (i)).

Sehen wir uns ein Beispiel für den zweiten, komplexeren Fall an: Wie viel muss ich investieren, um Zinsen für 30.000 € zu erhalten, mit einem Zinssatz von 8 % für 2 Jahre? Wir wenden die Formel „Anfangskapital = I ÷ (tx (i ÷ 100))“ an, was 30.000 ÷ (2 x (8 ÷ 100)) = 187.500 € Anfangsbetrag ergibt.
Wie wird der Zinssatz berechnet?
Um den Zinssatz zu berechnen, müssen wir ebenfalls die einfache Zinsformel verwenden, aber das i isolieren. Daher bleibt uns: Zinssatz (i) = Zins (I) ÷ (Anfangskapital (C) x Zeit (t)). Wie Sie sehen, sind alle Formeln gleich, isolieren jedoch eine andere Variable.
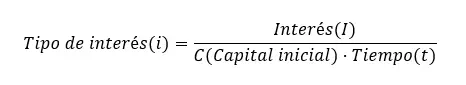
Hier ein praktischer Fall der Zinsberechnung: Zu welchem Zinssatz sollten wir 180.000 € für 5 Jahre anlegen, wenn wir daraus 200.000 € umrechnen wollen? In diesem Beispiel müssen Sie zunächst den Zinssatz ermitteln: I = Cf – C = 200.000 – 180.000 = 20.000 €. Und dann lösen wir: Zinssatz = 20.000 ÷ (180.000 x 5) = 0,022 x 100 = 2,2 %.
Wie wird die Zeit berechnet?
Schließlich können wir die Zeit berechnen, die auch aus der Anfangsformel erhalten werden kann: Zeit (t) = Zinsen (I) ÷ (Anfangsbetrag (C) x Zinssatz (i)). Es ist wichtig zu bedenken, dass die Formel Jahre als Zeiteinheiten erfordert. Wenn Sie es jedoch in anderen Einheiten ausdrücken möchten, können Sie die folgenden Variationen der Formel verwenden:
- I = C · (i / 100) · t, wenn t Jahre sind (Allgemeine Formel)
- I = C · (i / 1200) · t, wenn t Monate sind (Ergebnis in Monaten)
- I = C · (i / 36000) · t, wenn t Tage sind (Ergebnis in Tagen)
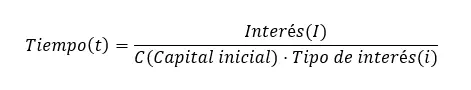
Schauen Sie sich das folgende Beispiel an: Wie viel Zeit muss vergehen, wenn wir wollen, dass eine Investition von 40.000 € einen Zins von 5.000 € bei einem Zinssatz von 5 % generiert? Es bleibt die Rechnung: Zeit = 5.000 ÷ (40.000 x 5 ÷ 100) = 2,5 Jahre. Wenn wir es jedoch in Monaten berechnen möchten, können wir Folgendes tun: Zeit = 5.000 ÷ (40.000 x 5 ÷ 1200) = 30 Monate.
Praxisbeispiel für eine einfache Zinsberechnung
Sie haben nun ein Beispiel für die Berechnung jeder Variablen gesehen, aus der die einfache Zinsformel besteht. Wir möchten Ihnen jedoch noch ein letztes Beispiel für die gebräuchlichste Berechnung zeigen, nämlich die des Zinses selbst. Für die Anwendung der ersten Formel bleiben Reste übrig. Falls Sie die Berechnung überprüfen möchten, finden Sie hier eine Fallstudie:
Wir leihen uns 10.000 € zum Investieren und wollen berechnen, wie viel Geld wir nach 5 Jahren zurückzahlen müssen, wenn man von uns 3 % Jahreszins verlangt. Die Berechnung wäre:
10.000 x 0,03 = 300
300 x 5 Jahre = 1.500 €
CF = 10.000 € + 1.500 € = 11.500 €
Somit würden die Zinsen am Ende von 5 Jahren 1.500 € und das endgültig einzuzahlende Kapital 11.500 € betragen .
Abschluss
Zusammenfassend lässt sich sagen, dass Sie zur Berechnung des einfachen Zinses die Kreditsumme, den Zinssatz und die Laufzeit berücksichtigen müssen. Von dort aus multiplizieren Sie einfach diese drei Zahlen, um den Gesamtbetrag der zu zahlenden Zinsen zu erhalten. Und wenn Sie statt des Zinses eine der anderen Variablen berechnen möchten, müssen Sie nur diesen Wert in der allgemeinen Formel isolieren.