Die mathematische Notation ist eine Möglichkeit, Ideen und Berechnungen mithilfe von Symbolen zu kommunizieren. Obwohl es auf den ersten Blick verwirrend erscheinen mag, können Sie es mit ein wenig Übung leicht interpretieren. In diesem Artikel zeigen wir Ihnen die Bedeutung aller in dieser Notation verwendeten Symbole und einige Beispiele für deren Anwendung.
Was ist mathematische Notation?
Die mathematische Notation ist eine Schreibweise für Werte und Ausdrücke, die in der Mathematik verwendet werden. Diese Technik ermöglicht es Mathematikern, Ideen prägnant und präzise auszudrücken. Die mathematische Notation ermöglicht auch denjenigen, die Mathematik praktizieren oder studieren, Konzepte besser zu verstehen.
Die Sprache der Mathematik sollte nicht mit der wissenschaftlichen Notation verwechselt werden, bei der es sich um eine Schreibweise numerischer Werte handelt. Mittlerweile besteht die mathematische Notation eher aus einer Reihe von Symbolen , die es Ihnen ermöglichen, komplexe Ausdrücke zu schreiben, genau wie eine Sprache. Wir werden später noch ausführlicher auf dieses Thema zurückkommen.
Wie liest man mathematische Notation?
Das Erlernen der mathematischen Notation ist einfacher als es scheint. Sie müssen nur die Bedeutung jedes Symbols lernen und dann können Sie alles lesen, was in mathematischer Notation geschrieben ist. So einfach ist das, obwohl es natürlich Übung und viel Lernzeit erfordert.
Mathematische Ausdrücke sind sehr logisch und folgen immer Mustern. Sie müssen sich daher nur die Regeln merken und wissen dann, wie Sie sie auf jede Situation übertragen können. Wir können sogar sehr komplexe Berechnungen beschreiben, das ist die Magie der mathematischen Sprache, die es ermöglicht, sehr komplexe Botschaften auf methodische Weise zu kommunizieren.
Komponenten der mathematischen Notation
Die mathematische Notation besteht aus einer Reihe von Symbolen , die Zahlen, Operationen und die Beziehungen zwischen ihnen darstellen. Diese Symbole mögen auf den ersten Blick kompliziert erscheinen, aber mit ein wenig Übung und Verständnis sollte die Interpretation der mathematischen Notation zum Kinderspiel werden.
Als nächstes erklären wir im Detail die vier Arten von Elementen, die in der mathematischen Sprache vorkommen. Beginnend mit dem Einfachsten und endend mit dem Komplexesten und Abstraktesten. Und sobald die theoretische Erklärung abgeschlossen ist, werden wir über die Arten der numerischen Notationen sprechen, die es gibt.
Zahlen und Zahlensätze
Zunächst müssen wir mathematische Zahlen definieren. Dabei handelt es sich um ein mathematisches Konzept, das eine auf eine Einheit bezogene Größe bezeichnet. Wir können jeden numerischen Wert beschreiben, indem wir dem dezimalen Zahlensystem folgen und die folgenden Symbole kombinieren: 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9.
Wenn wir Zahlen nach verschiedenen Eigenschaften ordnen, erhalten wir mehrere Kategorien von Zahlen, sogenannte Zahlenmengen. Und diese Wertegruppen haben auch eigene Symbole , die sie bezeichnen, in der folgenden Liste stellen wir sie alle mit dem Namen der entsprechenden Gruppe vor:
- ℙ: Primzahlen
- ℕ: natürliche Zahlen
- ℤ: Ganz
- ℚ: rationale Zahlen
- ℝ: Reelle Zahlen
- 𝕀: imaginäre Zahlen
- ℂ: komplexe Zahlen
- ℍ: Quaternionen
Diese Symbole werden im Allgemeinen in unseren Berechnungen verwendet, um einen großen Bereich von Zahlen auf einmal zu ermitteln. Wenn wir beispielsweise einen Ausdruck haben, der dementsprechend viele Werte akzeptiert, ist es für uns einfacher, diese Werte durch das Symbol anzugeben, das ihrer numerischen Gruppe entspricht, anstatt die Zahlen einzeln zu schreiben.
Operatoren und Quantoren
Nachdem wir nun über Zahlen gesprochen haben, die die Essenz der Mathematik darstellen, müssen wir über Operatoren und Quantoren sprechen. Das erste sind alle Symbole, die es uns ermöglichen, eine Operation darzustellen: Addition (+), Subtraktion (-), Multiplikation (x oder ·), Division (÷) und andere.
Wir haben jedoch auch zwei andere Arten von Operatoren, nämlich logische Operatoren und relationale Operatoren. Die erste drückt Konjunktion, Disjunktion und Negation aus. Sie helfen uns, logische Operationen vorzuschlagen, die im Gegensatz zu arithmetischen Operationen nicht mit Zahlen, sondern mit mathematischen Sätzen funktionieren.
Während die zweite es uns ermöglicht , Äquivalenzen und Beziehungen zwischen Werten oder mathematischen Ausdrücken herzustellen . Diese Symbole können in arithmetischen Berechnungen verwendet werden (um Zahlen zu ordnen), aber sie sind in der Algebra wichtiger, wenn wir Variablen haben (mehr dazu in zwei Abschnitten).
In der folgenden Liste finden Sie die Definition aller bisher besprochenen Operatoren:
| Symbol | Definition | Art |
| + | Zusatz | arithmetischer Operator |
| – | Subtraktion | arithmetischer Operator |
| X, *, · | Multiplikation | arithmetischer Operator |
| ÷ | Aufteilung | arithmetischer Operator |
| x² | Ermächtigung | arithmetischer Operator |
| √ | Kaution | arithmetischer Operator |
| UND | Verbindung | logischer Operator |
| ENTWEDER | Disjunktion | logischer Operator |
| NEIN | Verweigerung | logischer Operator |
| = | Gleich | Relationsoperator |
| > | Größer als | Relationsoperator |
| < | Kleiner als | Relationsoperator |
| >= | Besser als oder gleich | Relationsoperator |
| <= | Gleich oder kleiner als | Relationsoperator |
| ≠ | ist ungleich zu | Relationsoperator |
| ≡ | Genauso | Relationsoperator |
| ≈ | fast gleich | Relationsoperator |
| ≃ | Gleichwertig | Relationsoperator |
| ∝ | Proportional | Relationsoperator |
Allerdings gibt es noch fünf weitere logische Operatoren, die zur Erklärung der mathematischen Logik aus der Mengenlehre verwendet werden. Dabei handelt es sich um einen Zweig, der Mengenlogik anwendet, die in der Berechnung, Geometrie, Statistik usw. verwendet wird. Anschließend zeigen wir Ihnen die verwendeten Symbole und ihre Definition.
| Symbol | Definition |
| x ∈ A | x gehört zu A |
| x ∉ A | x gehört nicht zu A |
| ∪ | Union |
| ∩ | Überschneidung |
| ⊂ | Aufnahme |
Quantoren können wir als Symbole definieren, die die Anzahl der Elemente einer Menge angeben , die eine bestimmte Bedingung erfüllen (Äquivalenz, Reihenfolge, Zugehörigkeit usw.). Es gibt eine große Vielfalt an Operatoren, aber unter den am häufigsten verwendeten können wir Folgendes hervorheben:
| Symbol | Definition | Art |
| ∀x | für alle x | quantifizieren |
| ∃x | Es gibt mindestens ein x | quantifizieren |
| ∄x | es gibt kein x | quantifizieren |
| ∃!x | Es gibt nur ein x | quantifizieren |
| | | Wie zum Beispiel | quantifizieren |
| ∴ | ALSO | quantifizieren |
Mathematische Ausdrücke und ihre Beziehungen
Mit den Symbolen, die wir bisher behandelt haben, können Sie einen Großteil der Mathematik verstehen, aber wir haben ihre Anwendungen oder Beziehungen in komplexen Ausdrücken, wie kombinierten Operationen oder algebraischen Berechnungen, noch nicht erklärt. Außerdem gibt es immer noch Beziehungssymbole zu besprechen. Dies sind diejenigen, die wir in diesem Abschnitt sehen werden.
Beginnend mit den Gruppierungssymbolen sind dies Klammern, eckige Klammern und geschweifte Klammern. Diese Elemente sind bei der Bezeichnung komplexer Formeln von wesentlicher Bedeutung. Seine Hauptfunktion besteht darin, bestimmten Berechnungen innerhalb eines globalen Ausdrucks Priorität einzuräumen . Und es gibt unterschiedliche Prioritätsstufen zwischen den drei Typen. In diesem Ausdruck sehen Sie die Schreibreihenfolge 3 {[2 + (3 – 2) · 2] – 4}.
| Symbole | Definition | Priorität |
| „(„Und“)“ | Klammer | Maximale Priorität |
| „[„Und“]“ | Klammern | zweite Priorität |
| „{“ Und „}“ | Schlüssel | dritte Priorität |
Und um diese Kategorie abzuschließen, werden wir über Summationen (Σ) und Produkte (∏) sprechen, die Elemente sind, die es uns ermöglichen, wiederholte Additionen und Multiplikationen zu beschreiben. Die Summierung entspricht der Aussage: „Summe von Xi, wobei i die Werte von 1 bis an annimmt“. Und das Produkt ist dasselbe, aber statt zu addieren, multiplizieren wir.
algebraische Analyse
Das erste, was es über algebraische Symbole zu besprechen gilt, sind Variablen, die durch die Buchstaben des Alphabets dargestellt werden. Ihre Funktion besteht darin , eine Zahl nachzuahmen , sie haben jedoch keinen festen Wert wie mathematische Konstanten , sodass sie neue Werte annehmen können. Dies gilt für Gleichungen, Grenzwerte, Ableitungen, Integrale, Matrizen …
Abschließend wollen wir über die Darstellungen all dieser algebraischen Operationen sprechen, über die wir gerade in diesem letzten Absatz gesprochen haben. Seitdem bilden sie die Grundlage der Algebra und Sie müssen wissen, was ihre Symbologie ist. Als nächstes zeigen wir Ihnen eine Tabelle mit ihren verschiedenen Symbolen und einer kurzen Definition:
| Symbol | Definition |
| lim x → b | Grenze (wenn x in Richtung b tendiert) |
| y‘, ƒ‘ (x), dy / dx | Derivat |
| ∫ | Vollständig |
| Zu mxn | Matrix mit mxn-Dimensionen |
Fazit zu den Symbolen der mathematischen Sprache
Bisher haben Sie alle wichtigen Symbole gesehen, die in der Mathematik behandelt werden, aber es gibt natürlich noch mehr zu besprechen. Diese sind jedoch spezifischer für jede Unterkategorie der Mathematik: Geometrie, Statistik, Algebra … Wir schließen dieses Thema daher und sprechen über numerische Notationen.
Arten numerischer Notationen
In diesem Abschnitt werden wir alle Möglichkeiten sehen, mathematische Zahlen auszudrücken, da es dafür unterschiedliche Schreibweisen gibt. Zu Beginn haben wir oben das dezimale Zahlensystem erwähnt, das von Mathematikern am häufigsten verwendet wird. Als nächstes erklären wir es genauer und zeigen Ihnen weitere Arten der mathematischen Notation:
Dezimalschreibweise
Das Dezimalzahlensystem ist ein Positionszahlensystem (System, bei dem die Position jeder Ziffer ihren Wert bestimmt) und basiert auf den Vielfachen und Teilern der Zahl 10. Da zehn die Zahl ist, die als numerische Basis verwendet wird. Daher sind die zehn Zahlensymbole, die wir verwenden werden: 1, 2, 3, 4, 5, 6, 7, 8, 9 und 0.
Der Wert dieser Zahlen ergibt sich aus der Summe der Ziffern multipliziert mit den Potenzen zur Basis zehn, ermittelt entsprechend der Stellung . Und es ist sehr wichtig, dass Sie bedenken, dass Sie zum Schreiben einer Zahl kleiner als eins den Dezimalpunkt verwenden müssen. Nachfolgend finden Sie ein Beispiel:
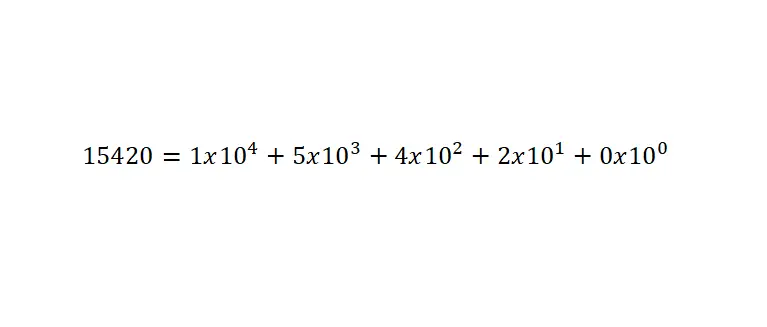
Wissenschaftliche Schreibweise
Die Exponentialschreibweise oder wissenschaftliche Notation ist eindeutig eine der am häufigsten verwendeten Schreibweisen in Wissenschaft und Technik. Dies ermöglicht es uns tatsächlich, sehr große und sehr kleine Zahlen auf einfache Weise auszudrücken. Um die Definition der wissenschaftlichen Notation zu verstehen, erklären wir, wie man dieser Notation eine ganze Zahl übergibt:
- Verschieben Sie den Dezimalpunkt: Sie müssen den Dezimalpunkt so oft wie nötig verschieben, bis Sie die erste Ziffer erreichen (nach links, wenn Sie eine sehr große Zahl haben, und nach rechts, wenn Sie eine sehr kleine Zahl haben).
- Legen Sie die Basis fest: Schreiben Sie diese letzte Zahl multipliziert mit zehn, also müssen Sie neben den Wert, den Sie durch Verschieben des Dezimalpunkts zur Seite erhalten, eine Multiplikation mit zehn schreiben: „x 10“.
- Fügen Sie einen Exponenten hinzu: mit einem Wert, der der Anzahl entspricht, wie oft Sie den Dezimalpunkt verschoben haben. Bei großen Zahlen belassen Sie den Exponenten positiv, bei kleinen Zahlen müssen Sie ihn jedoch mit negativem Vorzeichen schreiben.
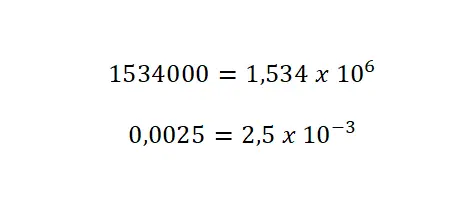
Hexadezimalschreibweise
Das Hexadezimalsystem basiert auf 16, was bedeutet, dass es sechzehn verschiedene Symbole verwendet: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E und F. Wie Sie können Sehen Sie, dieses Zahlensystem besteht aus den Zahlen des Dezimalsystems und sechs Buchstaben. Diese Schreibweise wird im Allgemeinen insbesondere in der IT und allem, was damit zu tun hat, verwendet.
Es ist wichtig klarzustellen, dass wir, da sie Symbole mit anderen Notationsarten gemeinsam hat, immer durch eine Klammer und den Index 16 angeben müssen, dass sie hexadezimal geschrieben ist. Im folgenden Beispiel sehen Sie anhand eines sehr anschaulichen Beispiels die Umwandlung einer Hexadezimalzahl in die Dezimalschreibweise:
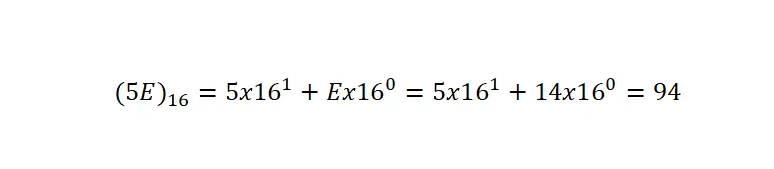
Um eine Hexadezimalzahl in einen Dezimalausdruck umzuwandeln, müssen wir die Zahl in ihre Basismultiplikationen zerlegen, wie wir es in der Dezimalschreibweise getan haben, aber die Basis auf 16 ändern. Als nächstes multiplizieren wir jede Ziffer mit sechzehn und erhöhen sie auf die Position, an der diese bestimmte Ziffer minus eins einnimmt.
Oktalschreibweise
Das letzte System, über das wir sprechen werden, ist die Oktalschreibweise mit der Basis 8. Das bedeutet, dass nur acht Symbole oder Zahlen verwendet werden: 0, 1, 2, 3, 4, 5, 6 und 7. wird am seltensten verwendet Nummerierungssystem aller von uns erklärten Elemente. Es ist zu beachten, dass Konvertierungen dieser Notation nach dem gleichen Verfahren wie die vorherigen durchgeführt werden.
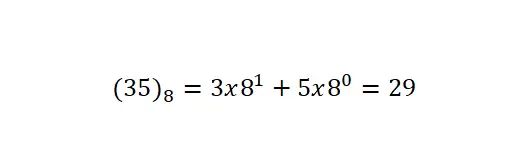
neuartige Notation
Abschließend können wir über das römische Zahlensystem sprechen, das heute nicht mehr weit verbreitet ist, aber in der Vergangenheit im Bereich der Mathematik sehr wichtig war. Denn es war eine der Notationen, die die Mathematik zum Leben erweckten.
Ihr Schreiben ist auf 7 Symbole beschränkt: I (1), V (5), X (10), L (50), C (100), D (500) und M (1000). Und durch die Kombination dieser Buchstaben werden alle Zahlen geschrieben. Wenn Sie wissen möchten , wie sie zusammenkommen , um andere größere Zahlen zu ergeben, empfehlen wir Ihnen, unseren Artikel darüber zu lesen, den Sie über den letzten Link aufrufen können.
Wie kann die Leseleistung in der mathematischen Notation verbessert werden?
Es gibt verschiedene Möglichkeiten, die Leistung beim Lesen der mathematischen Notation zu verbessern . Eine Möglichkeit besteht darin, die Symbole und Zahlen laut vorzulesen. Eine andere Möglichkeit besteht darin, sich mit den Symbolen und ihrer Bedeutung vertraut zu machen. Sie können das Lesen der mathematischen Notation auch anhand von Übungen und Aufgaben üben.
Wir hoffen, dass wir Ihnen mit diesem Leitfaden geholfen haben. Wenn Sie Fragen haben, zögern Sie bitte nicht, diese in den Kommentaren zu schreiben. Oder wenn Sie einen Beitrag zum Thema leisten möchten, freuen wir uns, dies auch in den Kommentaren zu sehen. Wir hinterlassen Ihnen jedoch einen Artikel über das Erlernen von Mathematik , falls Sie weiterlesen möchten.