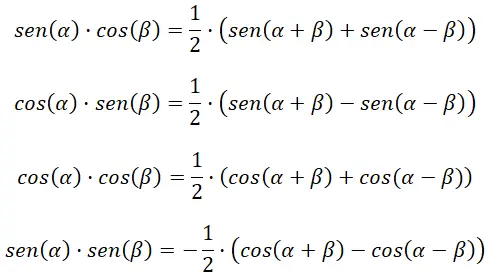Trigonometrische Identitäten sind Gleichheiten zwischen verschiedenen trigonometrischen Funktionen. Dank dieser trigonometrischen Äquivalenzen können wir aus jedem anderen ein bestimmtes trigonometrisches Verhältnis ableiten. Daher ist es notwendig, die Formeln dieser Verhältnisse zu kennen, um die Formeln trigonometrischer Identitäten zu verstehen. Wenn Sie diese in Ihrem Fall nicht kennen, empfehlen wir Ihnen, den letzten Link zu besuchen.
Tabelle der trigonometrischen Identitäten
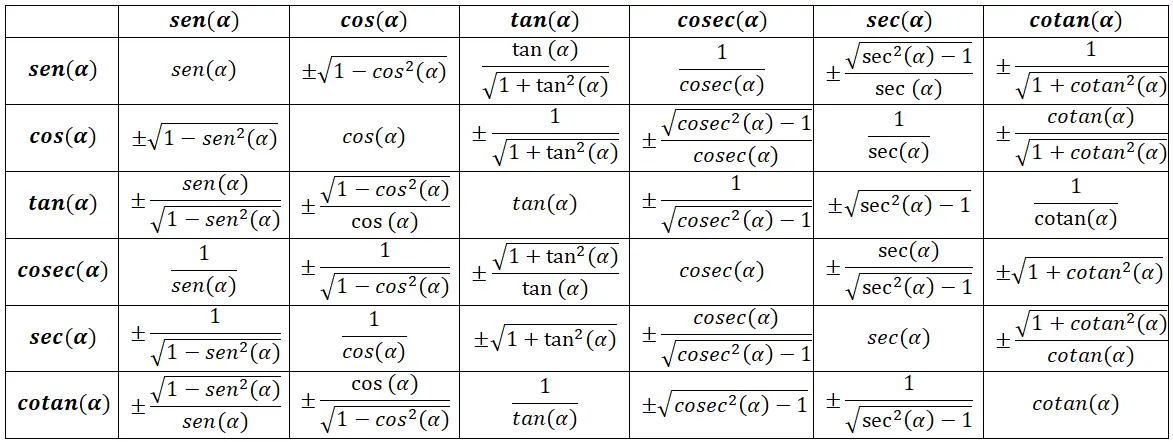
Grundlegende trigonometrische Identitäten
Es gibt eine Reihe grundlegender trigonometrischer Identitäten, die als die wichtigsten gelten, da sie die theoretische Grundlage für die anderen bilden. Diese sind am häufigsten zu finden und wahrscheinlich am einfachsten zu merken, da sie recht intuitiv sind. Denken Sie daran, dass alle Formeln auf dem folgenden Bild basieren:

Grundlegende trigonometrische Identität
Die erste Identität von allen ist die sogenannte grundlegende trigonometrische Identität , auch bekannt als die Beziehung zwischen Sinus und Cosinus. Unten ist der mathematische Beweis: sin² (α) + cos² (α) = 1.
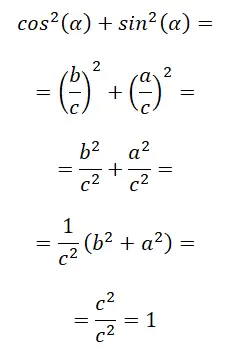
Im letzten Schritt wenden wir grundsätzlich den Satz des Pythagoras an, da c² = a² + b², dann bleibt c² / c² übrig, was gleich 1 ist. Zusammenfassend können wir Folgendes feststellen: sin² (α) + cos² (α) = 1.
Zusammenhang zwischen Sekante und Tangente (Sekante im Quadrat)
Zweitens haben wir eine trigonometrische Identität, die die Sekante mit der Tangente in Beziehung setzt. Ihr Ausdruck lautet wie folgt: sec² (α) = 1 + tan² (α) . Im folgenden Bild sehen Sie einige Erinnerungsformeln, aus denen sich diese Identität zusammensetzt, und anschließend die Vorgehensweise, die Sie befolgen müssen, um zur endgültigen Formel zu gelangen:
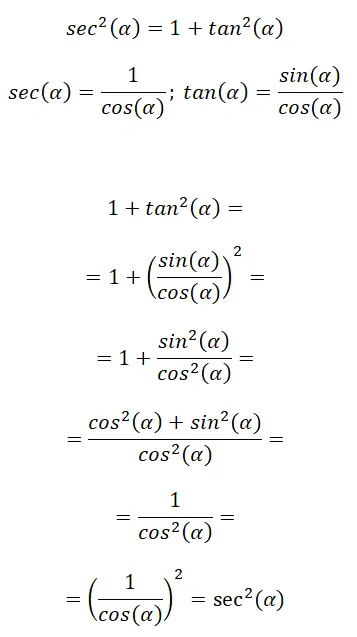
In diesem Fall verwenden wir die trigonometrischen Verhältnisformeln, um andere Verhältnisse zu finden. Zusammenfassend können wir sagen: sec²(α) = 1 + tan²(α).
Zusammenhang zwischen Kosekans und Kotangens (Kosekans im Quadrat)
Aus der Definition von Kosekans und Kotangens können wir einen Zusammenhang in der Tangensformel finden. Dadurch können wir eine weitere trigonometrische Identität ableiten: cosec² (α) = 1 + cotg² (α) .
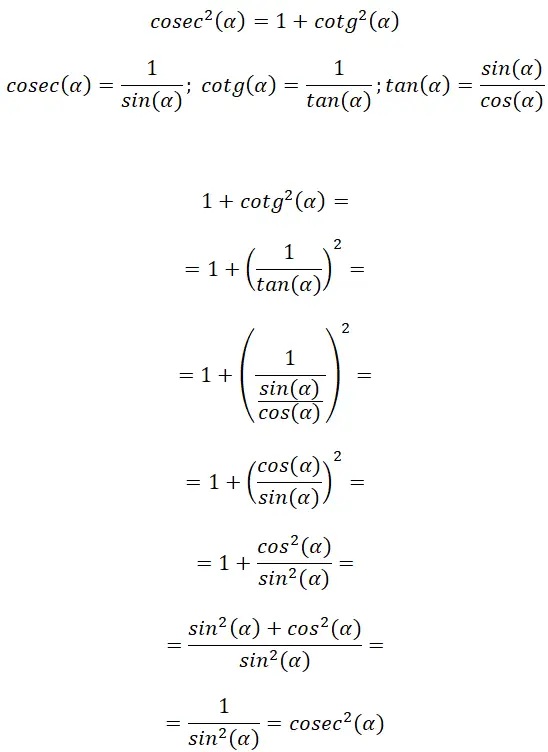
Mit dieser Demonstration können wir Folgendes überprüfen: cosec² (α) = 1 + cotg² (α). Darüber hinaus können wir erkennen, dass diese Beziehung eine gewisse Ähnlichkeit mit der vorherigen aufweist, was auf die Ähnlichkeit zwischen Tangens und Kotangens zurückzuführen ist.
Trigonometrische Verhältnisse von Summenwinkel und Subtraktionswinkel
Winkelsummen- oder Winkelsubtraktionsverhältnisse sind eine Art von Identitäten, die durch Berechnen der trigonometrischen Verhältnisse der Addition oder Subtraktion zweier Winkel erhalten werden. Wenn wir beispielsweise den Sinus von 90 + 60 berechnen möchten, gibt es eine Reihe von Formeln, die diese Berechnung erleichtern. Nachfolgend finden Sie eine Liste mit allen Formeln für trigonometrische Identitäten dieses Stils:
Sinus der Winkelsumme: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
Sinus der Winkelsubtraktion: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
Kosinus der Winkelsumme: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
Subtraktion des Winkelkosinus: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
Tangens der Winkelsumme: tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))
Winkeltangenssubtraktion: tan(α – β ) = (tan(α) + tan( β )) ÷(1 + tan(α)tan( β ))
Es ist offensichtlich, dass die Berechnung des Sinus von 150° einfacher ist als die Verwendung der Formeln, die wir gerade erklärt haben, um den Sinus von (90° + 60°) zu berechnen. Warum sind diese Formeln wichtig? Nun, die Antwort ist, dass diese Identitäten es uns ermöglichen, die trigonometrischen Verhältnisse komplexer Winkel aus einfacheren Winkeln zu berechnen. Wenn wir uns also die Verhältnisse der bemerkenswertesten (relevantesten) Winkel merken, müssen wir den Taschenrechner nicht verwenden, um die Verhältnisse komplexerer Winkel wie 150° zu berechnen.
Trigonometrische Verhältnisse mit doppeltem Winkel
Wenn wir die trigonometrischen Verhältnisse eines Doppelwinkels (2α) berechnen wollen, können wir dies mithilfe einer Reihe von Identitäten tun. Genauer gesagt können wir dies durch Formeln erreichen, die denen sehr ähnlich sind, die wir gerade im vorherigen Abschnitt besprochen haben. Denn wenn wir in den vorherigen Ausdrücken β in α ändern, bleibt (α + α) übrig, was äquivalent zu (2α) ist. Vor diesem Hintergrund können wir die folgenden Identitäten ableiten:
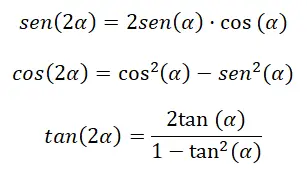
Sie können die Demos unten sehen:
Sinus des Doppelwinkels: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
Kosinus des Doppelwinkels: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
Doppeltangentenwinkel: tan (2α) = 2 tan (α) ÷ (1 – tan² (α))
Trigonometrische Verhältnisse des Halbwinkels
Außerdem gibt es Identitäten, die es uns ermöglichen, die trigonometrischen Verhältnisse des Halbwinkels (α/2) zu berechnen:
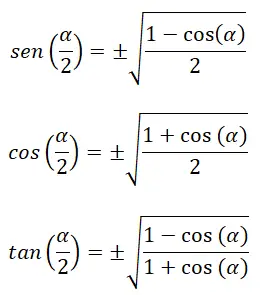
Unter den folgenden bereits bekannten Formeln:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
Wenn wir β = α/2 machen, können wir diese Identitäten beweisen, indem wir die beiden Ausdrücke im Fall des Sinus subtrahieren, sie im Fall des Kosinus addieren und die beiden erhaltenen Formeln (die des Sinus und die des Kosinus) dividieren. im Fall der Tangente. Es bleibt jedoch noch, das Verhältnis, das wir berechnen möchten, in den Formeln zu isolieren , die wir unten erhalten:
Halber Sinuswinkel: 1 – cos (α) = 2 sin² (α/2); sin² (α/2) = (1 – cos (α)) ÷ 2
Halbwinkelkosinus: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) ÷ 2
Trigonometrische Verhältnisse des Dreifachwinkels
Im Falle eines dreifachen Winkels (3α) können wir auch bestimmte Identitäten verwenden, um ihre trigonometrischen Verhältnisse zu berechnen. Diese Identitäten ergeben sich aus den folgenden bereits erläuterten Formeln: Doppelwinkelidentitäten, Summenwinkelidentitäten und der Grundidentität der Trigonometrie.
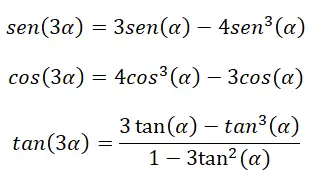
Um diese Identitäten zu beweisen, müssen wir die Winkelsummenformeln verwenden:
Sinus der Winkelsumme: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
Kosinus der Winkelsumme: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
Wenn wir also die Doppelwinkelformeln in den Ausdrücken, über die wir gerade gesprochen haben, anwenden und die grundlegende Identität der Trigonometrie anwenden, können wir die Identitäten beweisen. Es ist erwähnenswert, dass die Verwendung der grundlegenden trigonometrischen Identität es uns ermöglicht, alle Verhältnisse im Ausdruck in eins umzuwandeln. Deshalb besteht die Formel für den Sinus des Dreifachwinkels nur aus Sinuswerten und die des Cosinus nur aus Cosinuswerten. Unten sehen Sie den kompletten Ablauf:
Sinus des Dreifachwinkels: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= sin (α) – sin³ (α) – sin³ (α) + 2 sin (α) – 2 sin³ (α) =
= 3 sin (α) – 4 sin³ (α)
Kosinus des Dreifachwinkels: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos³ (α) – 3 cos (α) + 3 cos³ (α) =
= 4 cos³ (α) – 3 cos (α)
Schließlich kann der Tangens des Dreifachwinkels auf zwei Arten berechnet werden: erstens durch Division der Sinusformel durch die Kosinusformel und zweitens durch Einsetzen des Ausdrucks für den Tangens des Doppelwinkels in die folgende Formel für den Tangens des Summenwinkel: tan (α + 2α) = (tan (α) + tan (2α)) ÷ (1 – tan (α) tan (2α)).
Trigonometrische Identitäten nach Winkeltyp
Es ist wichtig, eine Reihe von Formeln zu kommentieren, bei denen es sich gewissermaßen um Regeln handelt, die die direkte und schnelle Berechnung trigonometrischer Verhältnisse ermöglichen. Tatsächlich können sie auch als trigonometrische Identitäten betrachtet werden, da sie dieselben Merkmale aufweisen wie alle Ausdrücke, über die wir gerade gesprochen haben. Genauer gesagt ermöglichen uns diese Formeln, die trigonometrischen Beziehungen eines Winkels aus der Beziehung zu einem anderen Winkel zu bestimmen.
ergänzende Winkel
Die Komplementärwinkel (α und β ) sind diejenigen, deren Summe 90° beträgt. Wenn wir sie also addieren, erhalten wir einen rechten Winkel. Um zu bestimmen, dass α der Komplementärwinkel von β ist, müssen wir eine sehr einfache Gleichung lösen: α = 90 – β . Wenn das Ergebnis dieser Äquivalenz übereinstimmt, können wir bestätigen, dass sie komplementär sind. Dank dieser Identitäten können wir die trigonometrischen Verhältnisse eines Winkels von denen des anderen ableiten.
Sinus des Komplementärwinkels: sin (90º – α) = cos (α)
Kosinus des Komplementärwinkels: cos (90º – α) = sin (α)
Tangens des Komplementärwinkels: tan (90º – α) = cotan (α)
Kosekans des Komplementärwinkels: cosec (90º – α) = sec (α)
Sekante des Komplementärwinkels: sec (90º – α) = cosec (α)
Kotangens des Komplementärwinkels: Cotan (90º – α) = tan (α)
zusätzliche Winkel
Die Zusatzwinkel (α und β ) sind diejenigen, deren Summe 180° oder π im Bogenmaß beträgt. Wir können daher die Formel α + β = 180° ableiten. Oder anders ausgedrückt: Wenn der Zusatzwinkel von α β ist, muss der folgende Ausdruck β = 180 – α erfüllt sein. Dann können Sie die Liste der Identitäten sehen, die wir aus diesen Blickwinkeln ableiten können:
Sinus des Zusatzwinkels: sin (180º – α) = sin (α)
Kosinus des Zusatzwinkels: cos (180º – α) = -cos (α)
Tangens des Ergänzungswinkels: tan (180º – α) = -tan (α)
Kosekans des zusätzlichen Winkels: cosec (180º – α) = cosec (α)
Sekante des Zusatzwinkels: sec (180º – α) = -sec (α)
Kotangens des Ergänzungswinkels: Cotan (180º – α) = -Cotan (α)
konjugierte Winkel
Die konjugierten Winkel (α und β ) sind solche, deren Summe 360° oder 2π im Bogenmaß beträgt, weshalb wir die Formel α + β = 360° ableiten können. Und aus dieser ersten Formel können wir einen der Winkel durch den anderen wie folgt ausdrücken: α = 360º – β oder β = 360º – α. Wir zeigen Ihnen nun die Gleichheiten konjugierter Winkel:
Sinus des konjugierten Winkels: sin (360º – α) = – sin (α)
Kosinus des konjugierten Winkels: cos (360º – α) = cos (α)
Tangens des konjugierten Winkels: tan (360º – α) = – tan (α)
Kosekans des konjugierten Winkels: cosec (360º – α) = – cosec (α)
Sekante des konjugierten Winkels: sec (360º – α) = sec (α)
Kotangens des konjugierten Winkels: Cotan (360º – α) = – Cotan (α)
entgegengesetzte Winkel
Entgegengesetzte Winkel oder negative Winkel (α und β ) sind solche, die den gleichen numerischen Wert, aber unterschiedliche Vorzeichen haben. Ein Beispiel für diesen Winkeltyp sind 30° und -30°. Es ist zu beachten, dass das negative Vorzeichen anzeigt, dass die Drehung im Uhrzeigersinn erfolgt, während ein positiver Winkel eine Drehung gegen den Uhrzeigersinn anzeigt.
Sinus des entgegengesetzten Winkels: sin (-α) = – sin (α)
Kosinus des entgegengesetzten Winkels: cos (-α) = cos (α)
Tangente des entgegengesetzten Winkels: tan (-α) = – tan (α)
Kosekans des entgegengesetzten Winkels: cosec (-α) = – cosec (α)
Sekante des entgegengesetzten Winkels: sec (-α) = sec (α)
Kotangens des entgegengesetzten Winkels: Cotan (-α) = – Cotan (α)
Winkel, die von 90° abweichen oder Winkel plus/minus π/2
Winkel, die sich um 90° unterscheiden, oder Winkel plus/minus π/2 (α und β ), sind solche, die einen Unterschied von 90° haben. Daher können sie als β – α = 90º ausgedrückt werden, wobei β 90º größer als α ist. Für diese Winkel gibt es auch eine Reihe von Formeln, die die trigonometrischen Verhältnisse der beiden Winkel in Beziehung setzen.
Sinus des Winkels, der von 90° abweicht: sin (90° + α) = cos (α)
Kosinus des Winkels, der von 90º abweicht: cos (90º + α) = -sin (α)
Tangens des Winkels, der von 90º abweicht: tan (90º + α) = – cotan (α)
Kosekans des Winkels, der von 90º abweicht: cosec (90º + α) = sec (α)
Sekante des Winkels, der von 90º abweicht: sec (90º + α) = -cosec (α)
Kotangens des Winkels, der von 90° abweicht: Cotan (90° + α) = -Cotan (α)
Winkel, die von 180° abweichen oder Winkel plus/minus π
Die Plus-/Minuswinkel π (α und β ) entsprechen Winkeln, die sich um 180° unterscheiden. Daher können sie mit der folgenden Formel ausgedrückt werden: β – α = 180º, wobei β 180º größer als α ist. Als nächstes zeigen wir Ihnen die trigonometrischen Identitäten, die die trigonometrischen Verhältnisse dieser Winkel in Beziehung setzen:
Sinus des Winkels, der von 180º abweicht: sin (180º + α ) = -sin ( α )
Kosinus des Winkels, der von 180º abweicht: cos (180º + α ) = -cos ( α )
Tangens des Winkels, der von 180º abweicht: tan (180º + α ) = tan ( α )
Kosekans des Winkels, der von 180º abweicht: cosec (180º + α ) = -cosec ( α )
Sekante des Winkels, der von 180º abweicht: sec (180º + α ) = -sec ( α )
Kotangens des Winkels, der von 180º abweicht: Cotan (180º + α ) = Cotan ( α )
Transformationen trigonometrischer Verhältnisse
Schließlich gibt es trigonometrische Identitäten, die es uns ermöglichen, ein bestimmtes trigonometrisches Verhältnis durch andere Operationen auszudrücken. Wenn wir also eine Summe von Verhältnissen haben und diese als Produkt ausdrücken möchten, können wir auf diese Formeln zurückgreifen. Obwohl es leider nicht für jede Rechenoperation einen Ausdruck gibt, kann man nur von der Addition oder Subtraktion zum Produkt und umgekehrt übergehen.
Addition oder Subtraktion in Produkt umwandeln
Die folgenden vier Formeln helfen uns bei der Berechnung der Addition und Subtraktion trigonometrischer Funktionen:
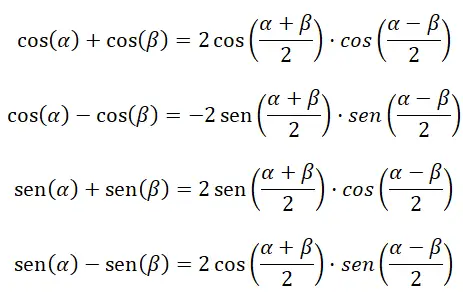
Wandeln Sie das Produkt in Addition oder Subtraktion um
Die folgenden vier Formeln helfen uns, die Produkte trigonometrischer Funktionen zu berechnen: