Polynomfunktionen

In diesem Artikel finden Sie eine sehr ausführliche Erklärung zu Polynomfunktionen , die durch Beispiele ergänzt wird. Darüber hinaus können Sie dank der Übungen, die wir Ihnen am Ende vorstellen, sehen, wie Polynomfunktionen im Alltag verwendet werden.

Was ist eine Polynomfunktion?

Polynomfunktionen oder Polynomfunktionen sind Funktionen, die durch einen einem Polynom äquivalenten algebraischen Ausdruck gegeben sind. Das bedeutet, dass der Ausdruck der Struktur eines Polynoms folgen muss: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ , abhängig von der Struktur, die wir verwenden werden Bestimmen Sie die Art der Polynomfunktion, die wir verarbeiten werden. Ein weiteres sehr relevantes Merkmal dieser Funktionen besteht darin, dass alle ihre Exponenten der Unbekannten positiv und ganze Zahlen sind.

Teile einer Polynomfunktion

Wir können drei wichtige Elemente in Bezug auf diese Funktionen hervorheben:

• Polynomkoeffizienten: Dies sind die Zahlen, die die Unbekannten begleiten, zum Beispiel ist die 3 des folgenden Termes ein Koeffizient: 3x ² . Es ist zu beachten, dass es genauso viele Koeffizienten gibt wie Terme im Polynom.
• Exponenten oder Indizes des Polynoms: Dies sind die Potenzen der Unbekannten, zum Beispiel ist die 2 des folgenden Termes ein Exponent: 3x ² . Und wie wir bereits erklärt haben, sind sie im Fall einer Polynomfunktion immer positiv und ganzzahlig.
• Grad des Polynoms: Dieser Wert entspricht dem Exponenten des höchsten Grades aller Terme, aus denen das Polynom besteht. Im Fall des Polynoms f(x) = 3x ² – 4x + 2 ist der Grad gleich zwei.

Woher wissen Sie, ob eine Funktion polynomisch ist oder nicht?

Um eine Polynomfunktion zu identifizieren, müssen wir prüfen, ob sie die Eigenschaften erfüllt, über die wir gerade gesprochen haben. Wir beginnen mit der Prüfung, ob der Ausdruck, der die Funktion definiert, eine Polynomstruktur hat: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ . Anschließend prüfen wir, ob die Indizes positiv und ganzzahlig sind. Mit diesen einfachen Schritten können wir feststellen, ob eine Funktion polynomisch ist oder nicht.

Arten von Polynomfunktionen mit Beispielen

Als nächstes zeigen wir Ihnen die verschiedenen Arten von Polynomfunktionen , die es gibt, die nach dem Grad des Polynoms klassifiziert werden. Zusätzlich finden Sie für jeden Typ eine beispielhafte grafische Darstellung. Dank dieser Beispiele für Polynomfunktionen können Sie die Unterschiede zwischen den verschiedenen Kategorien besser erkennen.

konstante Funktionen

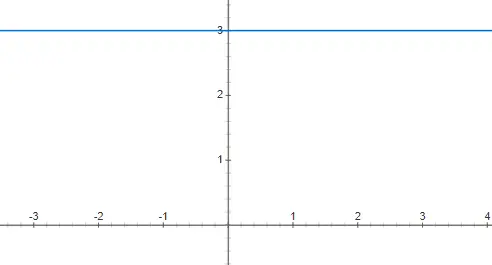
Konstante Funktionen entsprechen einem Polynom vom Grad 0, das heißt, der Koeffizient von x ist 0. Deshalb hängen Funktionen dieses Typs nicht vom Wert der unabhängigen Variablen x ab. Daher ist seine grafische Darstellung eine horizontale Linie, die unendlich ist. Nachfolgend finden Sie das Beispiel f(x) = 3 dargestellt:

Polynomfunktionen ersten Grades

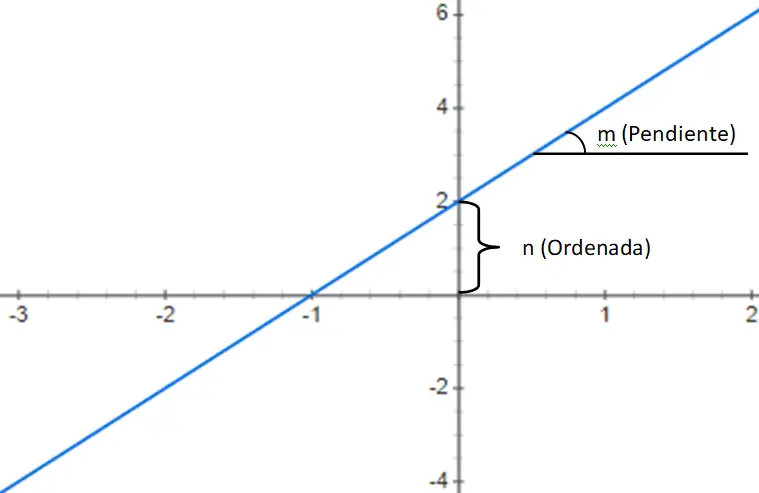
Zweitens finden wir die Polynomfunktionen ersten Grades , die durch ein Polynom 1. Grades mit der folgenden Struktur gegeben sind: f(x) = mx + n. Dieser Ausdruck besteht aus einer Zahl namens Steigung (m), die die Variable xy mit einer Konstante (n) multipliziert, die zu diesem Produkt addiert wird. Basierend auf den Werten von m und n können wir also drei verschiedene Arten von Funktionen identifizieren:

• Affine Funktionen: Dieser Untertyp zeichnet sich dadurch aus, dass er einen von 0 verschiedenen Wert von n aufweist, d der Ursprung. Beachten Sie auch, dass die Funktion abnimmt, wenn m < 0, während sie zunimmt, wenn m > 0.
• Lineare Funktionen: Der einzige Unterschied zwischen diesen Funktionen und affinen Funktionen besteht darin, dass n = 0 ist, sie also keinen Computer haben. Daher ist der Ausdruck für lineare Funktionen äquivalent zu f(x) = mx. Dieser Typ ist recht einfach darzustellen, da er immer durch den Punkt (0, 0) verläuft und wir aus der Steigung bereits den Graphen erhalten.
• Identitätsfunktionen: Dieser letzte Typ ist eine Untergruppe linearer Funktionen, für die an = 0 und m = 1 gilt. Dies bedeutet, dass der Ausdruck f(x) = x bleibt, wobei die grafische Darstellung eine Diagonale ist, die mit eine der Achsen. Diese Art von Funktion verläuft auch durch den Ursprungspunkt (0, 0).

Nachfolgend finden Sie ein Beispiel für eine Polynomfunktion ersten Grades, genauer gesagt eine affine Funktion f(x) = 3x + 2:

quadratische Funktionen

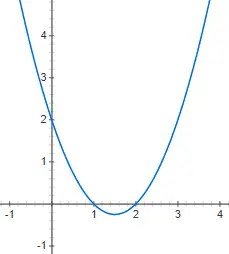
Quadratische Funktionen oder quadratische Funktionen werden durch quadratische Polynome ausgedrückt, die der Struktur folgen: f(x) = ax ² + bx + c, wobei a von 0 verschieden ist. In diesem Fall ist die grafische Darstellung viel komplexer, da sie es ist keine Gerade mehr, sondern eine vertikale Parabel . Nachfolgend finden Sie die Darstellung der quadratischen Funktion f(x) = 2x ² + 4x – 1:

Kubische Funktionen

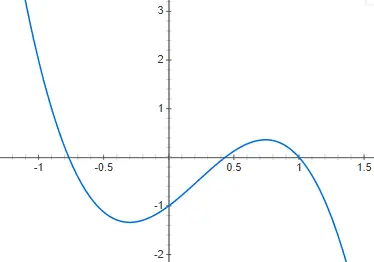
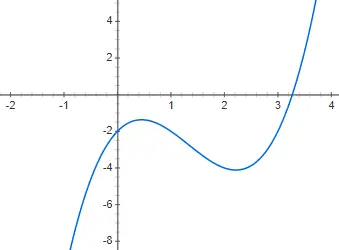
Kubische Funktionen oder Funktionen dritten Grades werden durch ein Polynom dritten Grades gegeben: f(x) = ax ³ + bx ² + cx + d, das von 0 verschieden ist. Die Darstellung einer Funktion dieses Stils ist noch komplexer als das des zweiten Grades, da es verschiedene Formen haben kann. Obwohl die Grundform, oder zumindest die gebräuchlichste, die ist, die wir Ihnen im folgenden Beispiel zeigen werden, f(x) = 2x ³ – 4x ² + 2x – 2:

Eigenschaften von Polynomfunktionen

Polynomfunktionen haben eine Reihe von Eigenschaften oder Merkmalen , die sie von anderen Funktionen unterscheiden. Wir werden sie im Folgenden so klar wie möglich beschreiben. Wenn Sie Funktionen wie diese sehen, können Sie sie auf diese Weise sehr leicht identifizieren:

• Der Definitionsbereich einer Polynomfunktion ist gleich allen reellen Zahlen : Dom f = R oder Dom f = (-∞, ∞), sie sind daher stetig über die gesamte Menge der reellen Zahlen.
• Sein Schnittpunkt auf der Y-Achse entspricht (0, a ₀ ), wobei ₀ der unabhängige Term ist.
• Schneidet entlang der X-Achse eine Anzahl von Malen, die gleich oder kleiner als der Grad des Polynoms sind.
• Polynomfunktionen haben keine Asymptoten.
• Wenn der Exponent aller Terme ungerade ist, ist der Graph symmetrisch zum Koordinatenursprung, während er, wenn der Exponent aller Terme gerade ist, symmetrisch zur OY-Achse ist.
• Die Anzahl der Wendepunkte einer Funktion dieses Stils ist gleich oder kleiner als n – 2, wobei n der Grad ist.
• Die Anzahl der relativen Maxima und Minima einer Funktion dieses Stils ist gleich oder kleiner als n – 1, wobei n der Grad ist.

Wie analysiert man eine Polynomfunktion?

Um eine Polynomfunktion zu analysieren, müssen wir das gleiche Verfahren anwenden, das wir für die Analyse jeder anderen Funktion verwenden würden. In der folgenden Liste haben wir die verschiedenen Elemente zusammengefasst, die untersucht oder behandelt werden müssen:

• Domäne und Bereich
• Schnittpunkte mit der horizontalen und vertikalen Achse
• Monotonie (zunehmend und fallend, Maxima und Minima)
• Krümmung (in Funktionen mit einem Grad größer als eins)

Natürlich können wir die Analyse auf eine andere Ebene bringen und viele andere Elemente untersuchen, obwohl dies ausreichen sollte. Denn wenn Sie diese Elemente kennen, haben Sie eine klare Vorstellung davon, wie die Funktion aussieht, und können sie grafisch darstellen.

Übungen zu Polynomfunktionen

Als nächstes bieten wir Ihnen eine Reihe von Übungen zum Üben der Darstellung von Funktionen , insbesondere von Polynomfunktionen. Auf diese Weise konsolidieren Sie alle in diesem Artikel erläuterten Konzepte:

Übung 1

Stellen Sie die folgende Polynomfunktion ersten Grades f(x) = x + 2 grafisch dar und sagen Sie, um welchen Typ es sich handelt:

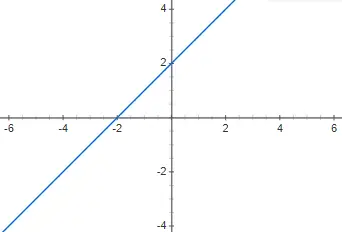
Es handelt sich um eine affine Polynomfunktion ersten Grades, da sie von 0 verschieden ist und m von 0 verschieden ist.

Übung 2

Zeichnen Sie die folgende quadratische Polynomfunktion f(x) = x ² + x – 2:

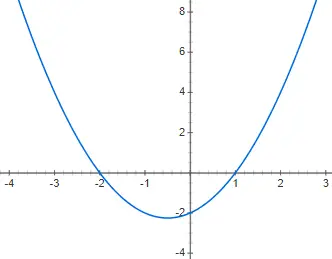
Übung 3

Stellen Sie die folgende Polynomfunktion dritten Grades f(x) = x ² + x – 2 grafisch dar: