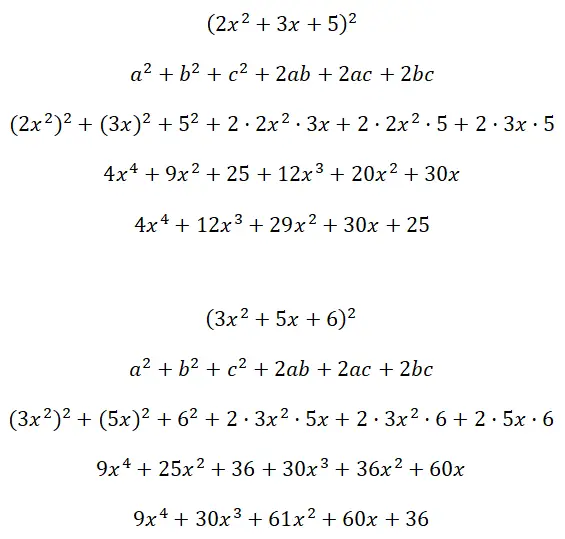Bemerkenswerte produkte

Was sind bemerkenswerte Produkte oder bemerkenswerte Identitäten?

Bemerkenswerte Identitäten , auch bemerkenswerte Produkte oder bemerkenswerte Gleichungen genannt, sind mathematische Ressourcen, die eine schnellere Lösung von Produkten und Quotienten von Polynomen ermöglichen. Wie das Wort Identität andeutet, handelt es sich hierbei um Gleichheiten, die es uns ermöglichen, diese Operationen zu berechnen, ohne sie lösen zu müssen. Da wir wissen, dass dieser Ausdruck festen Regeln folgt (die immer erfüllt sind), können wir das Ergebnis erhalten, ohne es überprüfen zu müssen.

Wann sollte eine bemerkenswerte Identität verwendet werden?

Diese Identitäten werden hauptsächlich im Bereich der Algebra verwendet und ihre Hauptfunktion besteht darin, die Lösung eines bestimmten Polynoms zu beschleunigen, ohne die gesamte Operation selbst lösen zu müssen. Von dort erhalten wir die Formeln bemerkenswerter Produkte, die wir im Laufe des Artikels kommentieren werden. Und schließlich können wir die Formeln auf vollständige Quadrate, Faktorpolynome oder jede andere Art von Berechnung anwenden.

Wie löst man ein bemerkenswertes Produkt Schritt für Schritt?

Um bemerkenswerte Identitäten aufzulösen, müssen Sie einem sehr einfachen Verfahren folgen, das auch sehr sinnvoll ist:

• Identifizieren Sie die Art der bemerkenswerten Identität: Der erste Schritt besteht darin, die Art der Operation zu identifizieren: ein bemerkenswertes Produkt oder ein bemerkenswerter Quotient. Sie sollten auch klären, welche Art von Formel Sie anwenden müssen. Dies werden Sie jedoch später verstehen, wenn wir die verschiedenen Arten bemerkenswerter Identitäten erläutert haben.
• Wenden Sie die Formel an: Sobald Sie wissen, welche Formel Sie anwenden müssen, ist es Zeit, die Berechnungen durchzuführen. Abhängig von der Art der Identität müssen Sie mehr oder weniger komplexe Operationen lösen und in den allermeisten Fällen bestehen diese Berechnungen aus Termen, die mindestens eine Unbekannte enthalten.
• Vereinfachen Sie den Ausdruck: Wenn Sie schließlich das Ergebnis erhalten, müssen Sie es vereinfachen. In diesem Schritt müssen Sie ähnliche Begriffe gruppieren und ordnen, um ein gut strukturiertes resultierendes Polynom zu bilden. Es ist zu beachten, dass dieser Schritt genauso wichtig ist wie die anderen, da sonst die Übung unvollständig bleibt.

Formeln bemerkenswerter Identitäten oder wichtiger bemerkenswerter Produkte

Nachfolgend finden Sie alle Formeln, die bemerkenswerten Identitäten entsprechen. Neben der theoretischen Erläuterung der einzelnen Fälle gibt es auch einige bemerkenswerte gelöste Produktbeispiele, anhand derer Sie alle Konzepte besser verstehen. Erwähnenswert ist, dass Sie in diesem ersten Abschnitt nur die wichtigsten Identitäten finden. Wenn Sie diesen Artikel lesen, erfahren Sie jedoch, wie Sie komplexere bemerkenswerte Produkte entwickeln, beispielsweise solche aus Trinomen.

Quadrat einer Summe

Der erste Fall betrifft das Quadrat der Summe , ein in der Welt der Algebra sehr verbreiteter Polynomausdruck. Dies kann wie folgt geschrieben werden: (a + b) ² , was äquivalent ist zu: (a + b) · (a + b). Daher wissen wir, dass es durch Polynommultiplikation gelöst werden kann. Aber dank bemerkenswerter Identitäten können wir Zeit sparen, indem wir die folgende Formel verwenden: (a + b) ² = a ² + 2ab + b ² . Als nächstes zeigen wir Ihnen die Demonstration der Formel , die wir gerade gesehen haben, damit Sie verstehen können, woher sie kommt und wie sie verwendet wird:

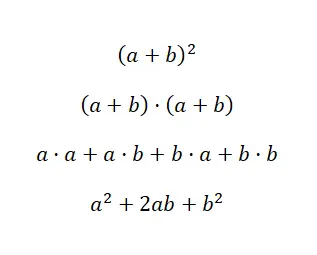
Wie wir sehen können, haben wir die Überprüfung mithilfe der Multiplikation von Polynomen durchgeführt, die wir zuvor kommentiert haben. Und wir können mit absoluter Sicherheit sagen: Wenn Sie die resultierende Formel auswendig kennen, können Sie durch eine einfache Wertesubstitution schneller zum Ergebnis gelangen. Es handelt sich also um ein sehr nützliches mathematisches Konzept. Nachdem Sie nun wissen, wie das Quadrat einer Summe funktioniert, zeigen wir Ihnen ein konkretes Beispiel:

Beispiel für das Quadrat einer Summe

Berechnen Sie die bemerkenswerte Identität (2x + 4) ² :

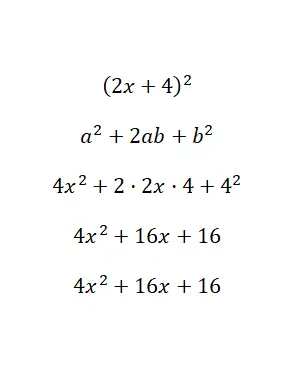
Im Grunde haben wir die Werte des Binomials mit den Buchstaben der Formel verknüpft und gelöst: a = 2x und b = 4. Schließlich, nachdem wir alle Berechnungen gelöst haben, erhalten wir das Polynom 4x ² + 16x + 16, das heißt entspricht dem Original . In diesem Beispiel haben wir aus einem reduzierten Polynom ein erweitertes Polynom (in Standardform) erhalten.

Quadrat einer Subtraktion

Ein weiterer sehr gebräuchlicher Ausdruck ist das Subtraktionsquadrat , das dem Additionsquadrat sehr ähnelt, sich jedoch nur um ein Vorzeichen ändert. Dann ist die Struktur des Binomials äquivalent zu: (a – b) ² , und wenn wir sie entfalten, erhalten wir: (a – b) · (a – b). Wie im vorherigen Fall kann dies aus einer Multiplikation von Polynomen berechnet werden, obwohl es auch eine Formel gibt, die die Lösung erleichtert: a ² – 2ab +b ² . Nachfolgend finden Sie den empirischen Beweis dafür:

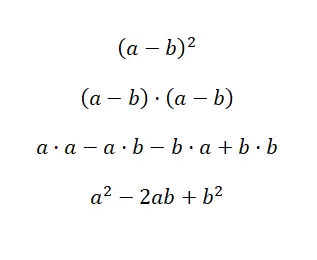
Um das Lösen des Quadrats einer Differenz zu vereinfachen, können wir dieselbe Formel verwenden, die wir für die Summe eines Quadrats verwendet haben, jedoch mit dem ersten Vorzeichen negativ . Diese minimale Änderung ermöglicht die Anpassung des Ausdrucks an Binome, die aus einem positiven Term und einem negativen Term bestehen, was für Subtraktionen nützlich ist. Wir zeigen Ihnen nun ein gelöstes Beispiel:

Beispiel für das Quadrat einer Subtraktion

Berechnen Sie die bemerkenswerte Identität (x – 3) ² :

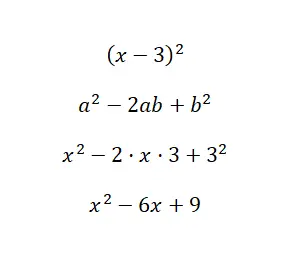
Wie Sie in der Beispiellösung sehen können, haben wir die Werte unseres Binomials in die Formel eingesetzt, a = x und b = 3. Daher müssen wir bei Verwendung der Formel, die wir zuvor erklärt haben, nur die Substitution und einige sehr grundlegende Dinge durchführen Berechnungen. Dadurch können wir sehen, wie einfach mit diesem Ausdruck das Quadrat einer Differenz berechnet werden kann.

Differenz von Quadraten oder Summe durch Differenz

Der dritte Fall bemerkenswerter Produkte wird Quadratdifferenz genannt. Diese wird durch das Produkt eines positiven Binomials und eines negativen Binomials gebildet. Ein Ausdruck dieses Stils hat die folgende Struktur: (a + b) · (a – b). Wenn wir also dieses Produkt erweitern, erhalten wir die Formel, die die Berechnung erleichtert: a ² – b ² . Wie Sie sehen, handelt es sich um eine sehr einfache Formel. Um sie jedoch vollständig zu verstehen, müssen Sie alle Berechnungen entwickeln:

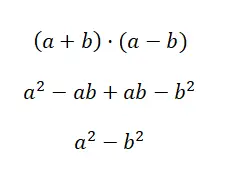
Beispiel für Summe durch Differenz

Berechnen Sie die bemerkenswerte Identität (x + 1) · (x – 4):

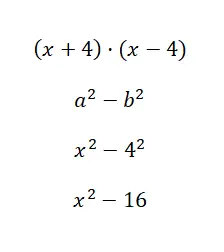
In diesem Fall ist die numerische Berechnung sehr einfach, tatsächlich mussten wir nur eine Potenz lösen. Zwar ist diese Formel nur anwendbar, wenn die Binome denselben Hauptterm und denselben unabhängigen Term haben, jedoch mit geändertem Vorzeichen. Diese Identität ist also wichtig, aber Sie werden sie nicht am häufigsten verwenden.

Produkt zweier Binome mit einem gemeinsamen Term

In diesem vierten Fall stehen wir vor einer Situation, die der vorherigen sehr ähnlich ist, allerdings mit einer geringfügigen Änderung in der Struktur. Beachten Sie den Unterschied, den wir Ihnen zeigen: (x + a) · (x + b) und (a + b) · (a – b). Falls Sie es immer noch nicht ganz klar sehen, betrachten Sie das folgende Beispiel: (x + 4) · (x + 5) und (x + 4) · (x – 4). Im ersten Fall (das Produkt zweier gemeinsamer Term-Binome ) gibt es nur einen gemeinsamen Term, während im zweiten Fall (die Summe durch Differenz) die beiden Terme gemeinsam sind, der unabhängige Term jedoch sein umgekehrtes Vorzeichen hat. Schauen wir uns nun an, mit welcher Formel wir vorgehen können:

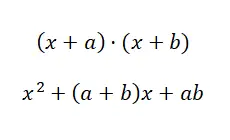
Beispiel für das Produkt zweier Binome mit einem gemeinsamen Term

Lösen Sie nach dem bemerkenswerten Produkt (x + 2) · (x + 3):

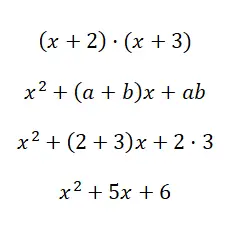
Mit der Formel x ² + (a + b)x + ab können wir das Polynom zweiten Grades berechnen, das sich aus der Multiplikation der beiden Binome ergibt . Wir hoffen, dass Sie anhand dieses Beispiels den Unterschied zwischen den letzten beiden von uns erläuterten Fällen verstanden haben, da es manchmal schwierig sein kann, sie zu unterscheiden.

Quadrat eines Trinoms

Wenn wir versuchen, das Quadrat eines Trinoms zu berechnen, haben wir auch ein bemerkenswertes Produkt, das uns das Leben erleichtert. Dieser Ausdruck wird wie folgt dargestellt: (a + b + c) ² und das entsprechende Produkt ist: a ² + b ² + c ² + 2ab + 2ac + 2bc. Es ist zu beachten, dass dies im Fall eines positiven Trinoms gilt, wenn jedoch einer der Koeffizienten negativ ist, müssen Sie nur den negativen Wert in die Formel schreiben. Nachfolgend finden Sie die Demonstration der Formel:

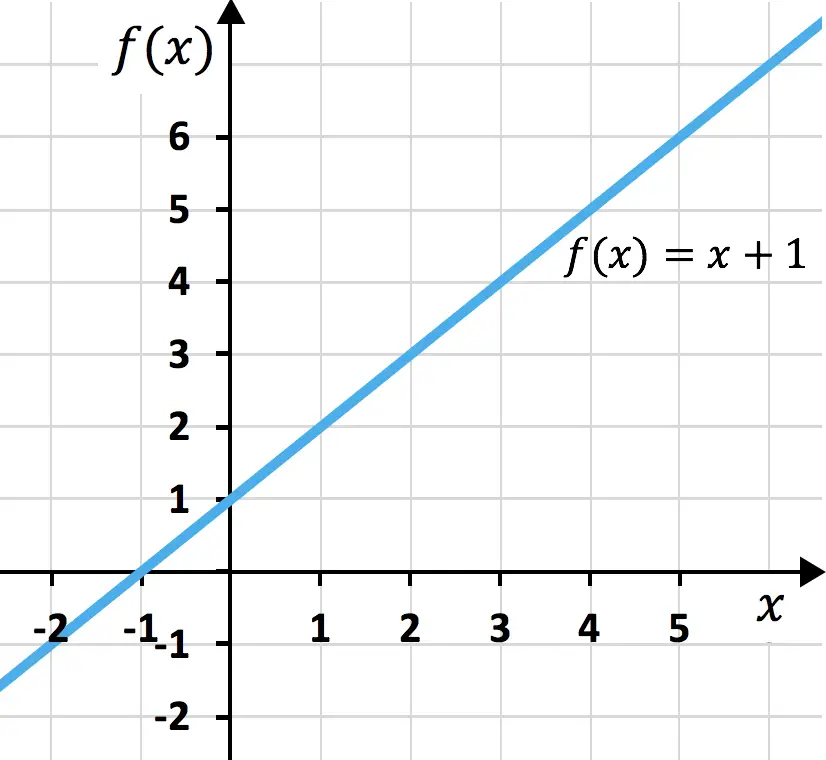
Beispiel für das Quadrat eines Trinoms

Berechnen Sie die bemerkenswerte Identität (2x + 1 + x ² ) ² :

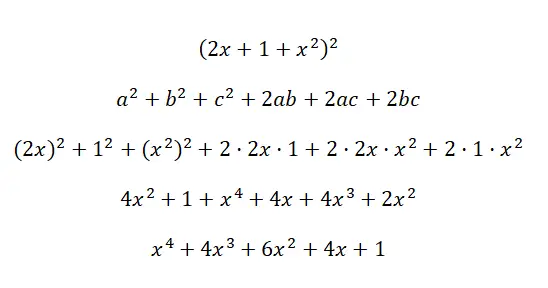
Bemerkenswerte Identitätsformeln oder bemerkenswerte Würfelprodukte

Nachdem wir nun die wichtigsten bemerkenswerten Identitäten erklärt haben, werden wir uns ihre Ableitungen ansehen, beginnend mit den kubischen Binomialen. Um bemerkenswerte Produkte dieses Stils zu berechnen, müssen wir auf etwas komplexere Formeln zurückgreifen, die jedoch einer ähnlichen Struktur folgen wie die bereits besprochenen.

Binomial gewürfelt

Die Kubikzahl eines Binomials wird geschrieben: (a + b) ³ und (a – b) ³ , dieser Ausdruck entspricht der folgenden Formel: (a ³ + 3a ² b + 3ab ² + b ³ ) und (a ³ – 3a ² b + 3ab ² – b ³ ). Diese beiden Fälle werden als Kubus einer Summe und Kubus einer Subtraktion bezeichnet, da es sich um kubische Binome handelt. Nachfolgend finden Sie eine sehr detaillierte Demonstration jedes Falles:

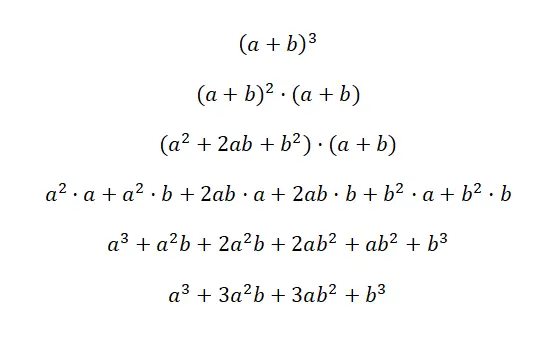
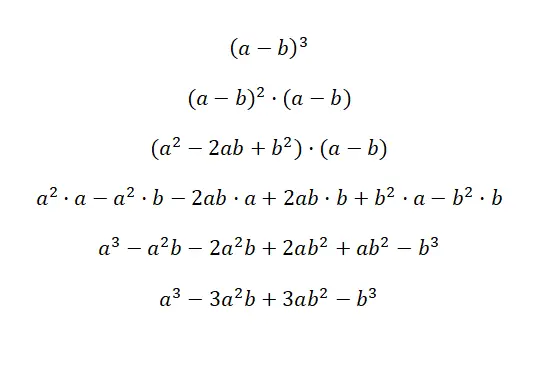
Der Schlüssel zum Verständnis dieses ersten Beweises besteht darin, zu verstehen, dass (a + b) ³ äquivalent ist zu: (a + b) ² · (a + b). Auf diese Weise verwenden wir die Formel für das Quadrat einer Summe , die wir zuvor erklärt haben, um den anderen Faktor zu multiplizieren. Dann vereinfachen wir einfach den Ausdruck und erhalten die entsprechende bemerkenswerte Identität: a ³ + 3a ² b + 3ab ² + b ³ . Im zweiten Beispiel passiert das Gleiche, allerdings mit einem Vorzeichenwechsel.

Beispiel eines Binomialwürfels

Bemerkenswerte Identität (x + 3) ³ lösen:

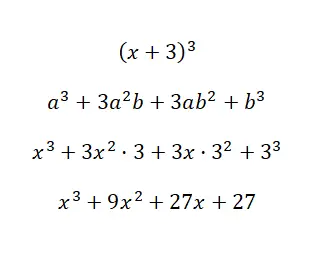
Mit der gerade besprochenen Formel können wir das Polynom berechnen und dabei Folgendes berücksichtigen: a = xyb = 3. Wie Sie sehen, ist das Verfahren sehr einfach und weist bei der Berechnung keine großen Komplikationen auf, da wir die Formel haben . Andernfalls wäre es ziemlich mühsam, so viele Multiplikationen durchführen zu müssen.

Summe der Würfel und Differenz der Würfel

Wir haben auch diesen anderen Fall, der leicht mit dem vorherigen verwechselt werden kann. Obwohl die beiden Fälle unterschiedlich geschrieben sind, sind sie nicht gleichwertig. Der Ausdruck, der der Summe oder Differenz der Würfel entspricht, ist: a ³ + b ³ , während wir im vorherigen Fall von (a + b) ³ gesprochen haben. Wie Sie sehen, besteht eine unbestreitbare Ähnlichkeit in der Struktur des Ausdrucks, aber in Wirklichkeit handelt es sich bei der Entwicklung der Berechnung um zwei völlig unterschiedliche Fälle:

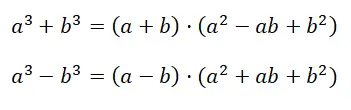
Bei der Demonstration der Formel erhalten wir die Faktorisierung des ersten Polynoms . Genauer gesagt gehen wir vom anfänglichen Binomial zum Produkt eines Binomials mit einem Trinom über. Es scheint, dass das erhaltene Ergebnis (a + b) · (a ² – ab + b ² ) die Berechnung überhaupt nicht vereinfacht, aber in Wirklichkeit erhalten wir durch Faktorisieren des Polynoms einen Ausdruck, der sehr leicht zu verstehen ist.

Beispiel einer Würfelsumme

Berechnen Sie das bemerkenswerte Produkt x ³ + 27:

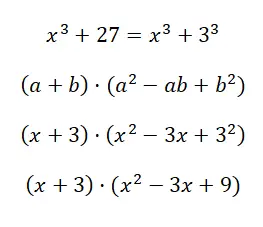
In diesem Fall ist das Ergebnis ziemlich lang, da es nicht weiter vereinfacht werden kann. Es ist jedoch normal, zu diesem Ausdruck zu gelangen. Tatsächlich kann man in diesen Fällen nur ein Ergebnis mit der Struktur erhalten, die dem Produkt eines Binomials mit einem Trinom entspricht , wie in diesem Beispiel.

trinomisch gewürfelt

Die Kubikzahl eines Trinoms wird geschrieben: (a + b + c) ³ , was auf die Multiplikation von drei identischen Trinomen hinausläuft, jedoch ohne Exponenten: (a + b + c) · (a + b + c) · (a + b + c). Es ist das komplexeste nennenswerte Produkt, das es gibt, obwohl die Formel ziemlich logisch ist und auf die gleiche Weise wie alle anderen erhalten wird, wenn man die entsprechenden Multiplikationen von Polynomen durchführt. Nachfolgend finden Sie den Beweis der Formel für diese bemerkenswerte Identität:

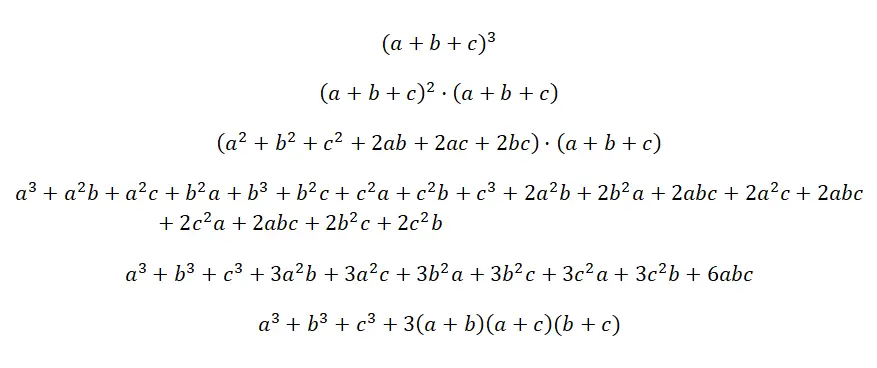
Beispiel für die Kubuszahl eines Trinoms

Lösen Sie den folgenden Trinomwürfel (x ² + 3x – 4) ³ :

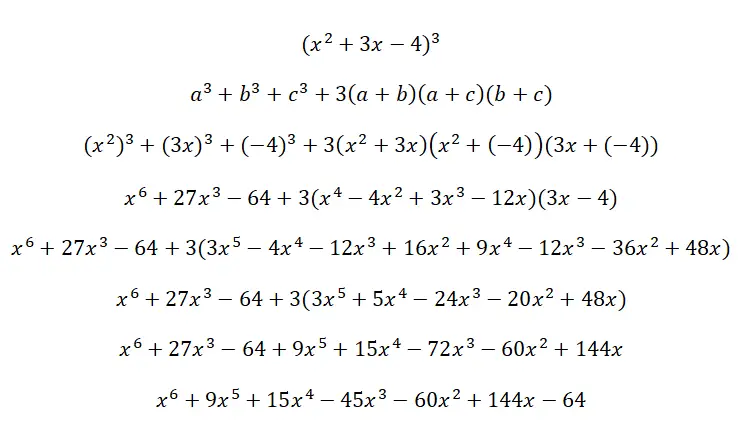
bemerkenswerte Verhältnisse

Abschließend erklären wir bemerkenswerte Quotienten , bei denen es sich um bemerkenswerte Identitäten zum schnellen Lösen bestimmter Arten algebraischer Brüche handelt. Genauer gesagt gibt es vier verschiedene Typen, die ein gemeinsames Merkmal haben: Ihr Ergebnis besteht aus exakten Polynomen (mit einem Rest gleich Null). Erwähnenswert ist auch, dass die Formeln bemerkenswerter Quotienten eine gewisse Beziehung zu den Formeln bemerkenswerter Produkte haben, die wir bereits erklärt haben.

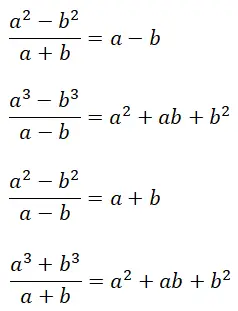
Beispiel für die Lösung bemerkenswerter Verhältnisse

Berechnen Sie die folgenden bemerkenswerten Verhältnisse:

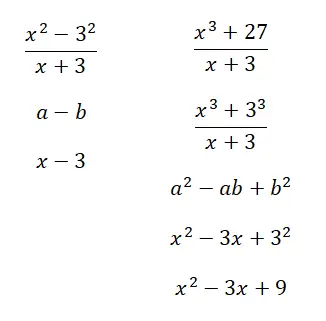
Bemerkenswerte Produktübungen gelöst

Nachdem Sie nun wissen, wie die verschiedenen Notables aufgelöst werden, ist es an der Zeit, ein wenig zu üben. Aus diesem Grund bieten wir Ihnen 6 Übungen an, um die gesamte erläuterte Theorie anzuwenden. Und wir zeigen Ihnen eine Tabelle mit den wichtigsten bemerkenswerten Identitäten, damit Sie sie beim Lösen aller Übungen zur Hand haben:

Übung 1

Lösen Sie die Binomialquadrate (x – 4) ² , (x + 1) ² und (x – 3) ² :

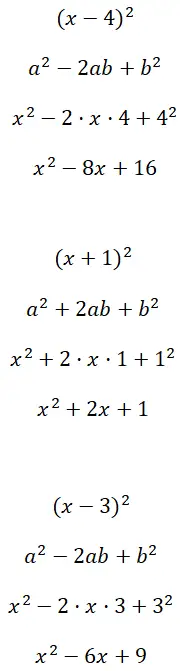
Übung 2

Berechnen Sie die beiden Differenzen der Quadrate (x – 1) · (x + 1) und (x + 3) · (x – 3):

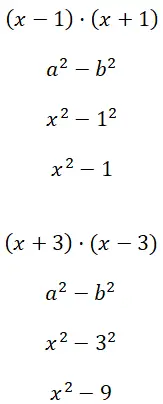
Übung 3

Entwickeln Sie die bemerkenswerten Produkte zum Würfel (x – 5) ³ und (x + 8) ³ :

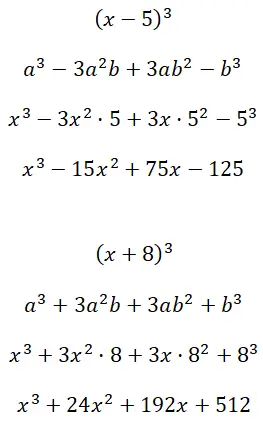
Übung 4

Entwickeln Sie bemerkenswerte Identitäten, die aus Multifaktor-Termen (4x ² + 5y) ² , (5x ³ + y ² ) · (5x ³ – y ² ) und (5xy ² – 2xy) ² gebildet werden:

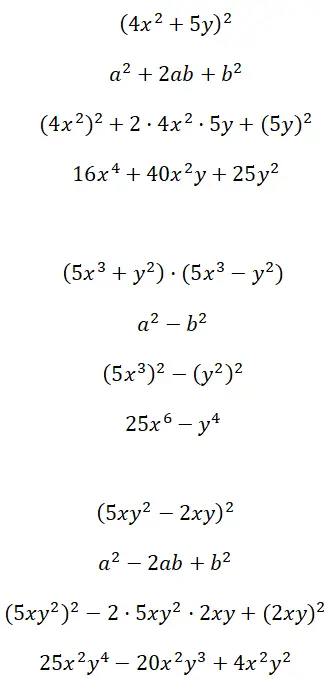
Übung 5

Berechnen Sie die bemerkenswerten kubischen Produkte, die durch die Multifaktorterme (3x ² + y) ³ und (5y ³ – 2x ² ) ³ gebildet werden:

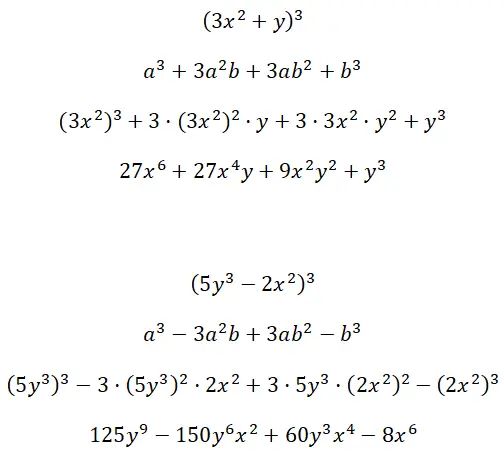
Übung 6

Lösen Sie die Quadrate der Trinome (2x ² + 3x + 5) ² und (3x ² + 5x + 6):