Ein irreduzibler Bruch ist ein Bruch, der nicht weiter vereinfacht werden kann und daher keine kleineren äquivalenten Brüche hat. Mit anderen Worten, der gcf von Zähler und Nenner eines irreduziblen Bruchs ist gleich 1, da sie keine anderen gemeinsamen Teiler haben. Zum Beispiel kann der Ausdruck „5/8“ nicht mehr reduziert werden, daher sagen wir, dass er in seiner einfachsten Form vorliegt oder dass er irreduzibel ist.
Rechner für irreduzible Brüche
Bevor wir mit der Theorie fortfahren, möchten wir Ihnen einen Rechner zeigen, mit dem Sie den irreduziblen Bruch einer beliebigen gemischten Zahl ermitteln können. Sie müssen lediglich die Werte von Zähler und Nenner eingeben und auf „Bruch vereinfachen“ klicken, dann erhalten Sie im Ergebnisfeld die reduzierte Form. Wir empfehlen, dieses Tool zu verwenden, um jeden Bruch sofort zu vereinfachen oder sogar Ihre Bruchübungen zu korrigieren.
Was ist ein irreduzibler Bruch und wie wird er berechnet?
Wie wir eingangs bereits erklärt haben, ist ein irreduzibler Bruch ein Bruch, der sich nicht weiter vereinfachen lässt, es handelt sich also um einen unmittelbaren Bruch . Wenn Sie diese Art von Brüchen finden möchten, müssen Sie die Vereinfachung von Brüchen verwenden. Auf diese Weise finden Sie einen äquivalenten Bruch, der in Bezug auf den Anfangsbruch irreduzibel ist. Unter diesem letzten Link finden Sie eine detaillierte Anleitung zum Vereinfachen von Brüchen. In der folgenden Liste erklären wir die Schritte jedoch zusammenfassend:
- Gemeinsame Faktoren finden: Zunächst müssen Sie den größten gemeinsamen Faktor von Zähler und Nenner ermitteln. Auf diese Weise erhalten Sie eine Zahl, die es Ihnen ermöglicht, beide Werte zu reduzieren und gleichzeitig die Äquivalenz beizubehalten.
- Teilen Sie den reduzierbaren Bruch durch den gcf: Sobald Sie den gcf haben, müssen Sie Zähler und Nenner durch diesen gemeinsamen Teiler dividieren. Dadurch erhalten Sie einen einfacheren (oder kleineren) äquivalenten Zähler und Nenner.
Sie können auch andere Methoden verwenden, um irreduzible Brüche zu finden, die in unserem Artikel über die Vereinfachung von Brüchen erläutert werden. Obwohl Sie mit dieser Methode, die wir Ihnen erklärt haben, jeden gewünschten Bruch sehr einfach und schnell reduzieren können.
Beispiel für reduzierbare Brüche und irreduzible Brüche
Im folgenden Bild finden Sie vier Beispiele für reduzierbare Brüche und vier weitere für irreduzible Brüche. Wir empfehlen Ihnen, jeden der Brüche zu vereinfachen, damit Sie den Unterschied zwischen den beiden Arten von Brüchen klar verstehen.
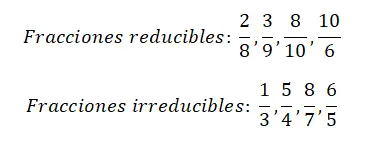
Beispiel für die Berechnung eines irreduziblen Bruchs
Hier zeigen wir dir Schritt für Schritt, wie du einen Bruch mit zwei Methoden vereinfachen kannst. Das erste zeigt den vollständigen Vorgang, den wir im vorherigen Abschnitt erklärt haben. Und das zweite zeigt ein etwas anderes System, bei dem Zähler und Nenner durch denselben Wert dividiert werden, beginnend mit dem kleinsten Teiler (ohne 1 zu zählen) und dann hochgearbeitet. Wenn Sie jedoch der Meinung sind, dass das zweite System zu kompliziert ist, können Sie es ignorieren.
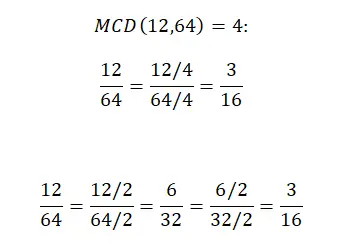
Irreduzibler Bruchteil einer Dezimalzahl
Der aus einer Dezimalzahl erhaltene irreduzible Bruch wird Erzeugerbruch genannt. Es ist wichtig zu beachten, dass die Berechnung je nach Art der Dezimalzahl (exakt, rein periodisch oder gemischt periodisch) auf unterschiedliche Weise erfolgt. Das folgende Beispiel zeigt dieses mathematische Konzept deutlich: 5/7 = 0,7142857... Wie Sie sehen können, sind fünf Siebtel der irreduzible Bruch, der der Dezimalzahl 0,7142857 entspricht...
Wie erkennt man, ob ein Bruch irreduzibel ist?
Um herauszufinden, ob ein Bruch reduzierbar oder irreduzibel ist, können Sie zwei Methoden anwenden. Die erste besteht darin, den größten gemeinsamen Teiler von Zähler und Nenner zu berechnen. Wenn dieser Wert von eins abweicht, bedeutet dies, dass es sich um einen reduzierbaren Bruch handelt. Und wenn Sie als Ergebnis eins erhalten, wissen Sie, dass der Bruch irreduzibel sein wird. Zweitens können Sie den Rechner für irreduzible Brüche verwenden, den wir Ihnen zu Beginn gezeigt haben, um diese Art von Prüfungen durchzuführen.
Aufgaben zu irreduziblen Brüchen gelöst
Nachdem Sie die Theorie gelesen haben, empfehlen wir Ihnen, diese Probleme zu lösen , damit Sie die Berechnung irreduzibler Brüche üben können. Wenn Sie außerdem Ihr Verständnis für gemischte Zahlen verbessern möchten, empfehlen wir Ihnen, diese Bruchübungen zu lösen. Dadurch werden Sie das Konzept des Bruchs selbst besser verstehen.
Übung 1
Berechnen Sie den irreduziblen Bruch der folgenden reduzierbaren Brüche. Denken Sie daran, dass Sie jede Methode zur Vereinfachung von Brüchen verwenden können. Und wenn Sie die Übung beendet haben, können Sie Ihre Ergebnisse mit denen vergleichen, die wir Ihnen im Bild unten zeigen.
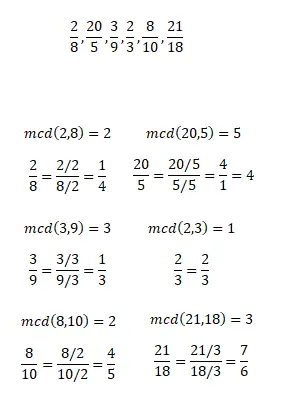
Übung 2
Identifizieren Sie die Brüche, die den irreduziblen Brüchen 2/3 und 4/5 entsprechen. Um diese Aufgabe abzuschließen, empfehlen wir, sich die Zahlen im Zähler und Nenner anzusehen und über die Teilbarkeitsbeziehung nachzudenken, die sie haben. Vielleicht können Sie den größten gemeinsamen Faktor oder das kleinste gemeinsame Vielfache verwenden, um das Gesuchte zu finden ...
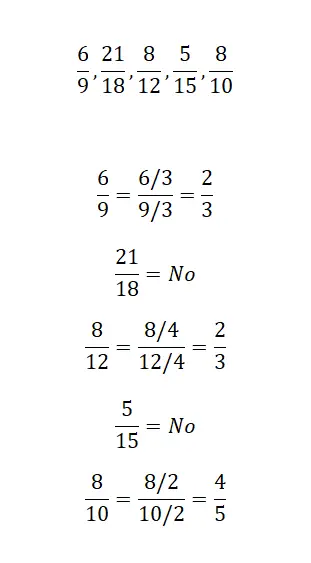
Übung 3
In dieser letzten Übung müssen Sie nur angeben, ob die folgenden drei Brüche denselben irreduziblen Bruch haben. Daher ist es notwendig, die drei Brüche so weit wie möglich zu reduzieren und das Ergebnis zu analysieren. Sobald Sie es gelöst haben, können Sie Ihre Lösungen mit unseren vergleichen.
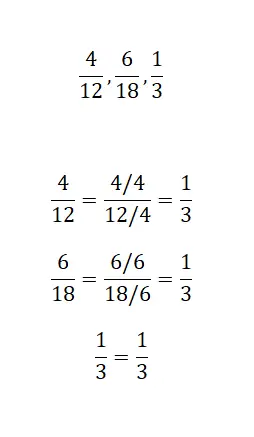
Weitere Informationen zu Brüchen
Wir hoffen, dass dieser Artikel Ihnen geholfen hat, irreduzible Brüche zu verstehen. Wenn Sie jedoch Fragen haben, können Sie gerne unsere Erklärung zu Brüchen lesen. Dort finden Sie alle Informationen zu Brüchen: Definition, Kategorien, Operationen und Übungen, alles erklärt anhand von Theorie und Beispielen. Wir versichern Ihnen, dass Sie durch die Lektüre dieses Artikels viele grundlegende Zweifel im Zusammenhang mit diesem Thema ausräumen werden.