Das Vereinfachen von Brüchen oder das Reduzieren von Brüchen ist ein mathematisches Verfahren, das darauf abzielt, einen komplexen Bruch in einen anderen einfacheren äquivalenten Bruch umzuwandeln. Dies ermöglicht es uns daher, den irreduziblen Bruchteil des ursprünglichen Ausdrucks zu finden, und dies kann mit verschiedenen Methoden erfolgen. Bevor Sie sie jedoch erklären, empfehlen wir Ihnen, den Rechner zur Vereinfachung von Brüchen auszuprobieren, den Sie direkt unter diesem Text finden.
Online-Bruchvereinfachung
Mit dem folgenden Online-Rechner zur Vereinfachung von Brüchen können Sie gemischte Zahlen jeglicher Art kürzen. Sie müssen lediglich die Werte von Zähler und Nenner eingeben und dann auf die Schaltfläche „Vereinfachen“ klicken. Sobald Sie das getan haben, erhalten Sie den vereinfachtesten Ausdruck.
Wie vereinfacht man einen Bruch?
Wie bereits erwähnt, geht es bei der Vereinfachung von Brüchen darum, den irreduziblen Bruch eines komplexeren Bruchs zu finden. Derzeit haben wir zwei Methoden , um Brüche zu vereinfachen: Die erste besteht darin, normale Divisionen zu verwenden, und die zweite darin, einen gemeinsamen Faktor zu extrahieren.
Brüche durch Division vereinfachen
Dieses System besteht darin, sowohl den Zähler als auch den Nenner durch gemeinsame Teiler (außer 1) zu dividieren, bis wir keinen gemeinsamen Teiler mehr haben. Auf diese Weise erhalten wir einen irreduziblen Bruch. Um den Teiler auszuwählen, den wir in jeder Division verwenden, können wir dies auf zwei verschiedene Arten tun: Die erste besteht darin, gemeinsame Teiler zu verwenden, bis wir die einfachste Form dieses Bruchs erhalten, und die zweite darin, den größten gemeinsamen Teiler von zu berechnen Zähler und Nenner.
Wenn wir beispielsweise den Bruch 12/64 vereinfachen möchten, können wir dies tun, indem wir Zähler und Nenner durch den gcf beider dividieren oder indem wir beide Teile des Bruchs durch dieselbe Zahl dividieren, bis wir zunächst einen irreduziblen Bruch erhalten mit den kleinsten Teilern (ohne 1) und aufwärts arbeitend. Unten sehen Sie, wie beide Methoden Schritt für Schritt gelöst werden:
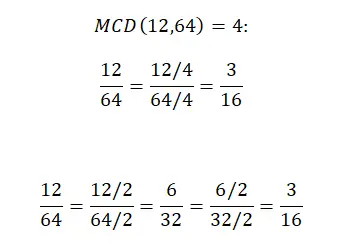
Vereinfachung von Brüchen durch Extraktion gemeinsamer Faktoren
Um diese andere Methode durchzuführen, müssen wir den Zähler und den Nenner in Primzahlen zerlegen. Und wir werden das Produkt äquivalenter Potenzen durch die ursprünglichen Zahlenwerte ersetzen. Als nächstes reduzieren wir den Ausdruck, indem wir die Potenzen mit einer gemeinsamen Basis vereinfachen und dabei die Eigenschaften der Potenzen verwenden. Wir vereinfachen nun einen Beispielbruch mit dieser Methode:
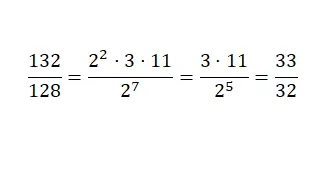
Brüche, die schwer zu reduzieren sind
Als nächstes werden wir einige Zweifel bezüglich der komplexesten Fälle der Vereinfachung ausräumen. Auf diese Weise können Sie jeden Bruch, der Ihnen vorgeschlagen wird, reduzieren. Obwohl dieser Abschnitt eher optional ist, können Sie, wenn Sie mit dem Üben beginnen möchten, zum letzten Abschnitt springen:
Brüche mit Exponenten vereinfachen
Um diese Art von Brüchen zu vereinfachen, müssen wir den Exponentenausdruck als einen einzelnen numerischen Wert schreiben. Zuerst können wir die Primfaktorzerlegung ausprobieren und dabei Zähler und Nenner vereinfachen. Und wenn wir noch keinen irreduziblen Bruch erhalten haben, dividieren wir die beiden Teile des Bruchs, bis wir einen Ausdruck erhalten, der nicht mehr reduziert werden kann. Wie Sie sehen, erfordert die Vereinfachung von Brüchen mit Potenzen die Kombination aller Methoden, über die wir im vorherigen Abschnitt gesprochen haben.
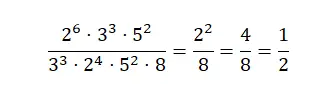
Vereinfachen Sie negative Brüche
Wenn wir negative Brüche vereinfachen möchten, können wir dies mit einer der drei zuvor erläuterten Methoden tun, da das Vorzeichen keinen direkten Einfluss auf das Berechnungsverfahren hat. Sie müssen nur eine einzige Änderung am Ergebnis vornehmen, nämlich das negative Vorzeichen hinzufügen. Aber alles andere ist genau das Gleiche. Damit Sie es sehen können, zeigen wir Ihnen unten das erste Beispiel, das wir gelöst erklärt haben, allerdings mit negativem Vorzeichen.
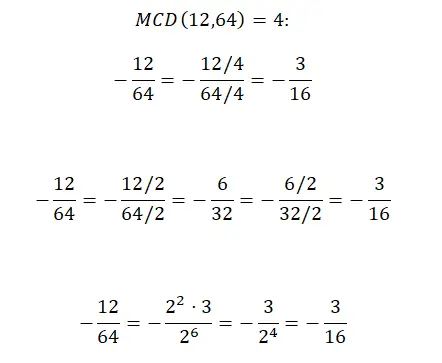
Brüche mit großen Zahlen vereinfachen
In diesem Fall empfehlen wir die Verwendung der Common Factor Extraction- Methode, da große Zahlen einfacher werden, wenn man sie in Primfaktoren ausdrückt. Dadurch ersparen Sie sich die Lösung vieler Divisionen, bis Sie zu einem irreduziblen Bruch gelangen. Obwohl Sie in Wirklichkeit jede Methode verwenden können, die Sie bevorzugen.
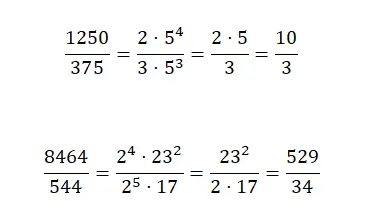
Wie vereinfacht man Brüche mit dem wissenschaftlichen Taschenrechner?
In vielen wissenschaftlichen Taschenrechnern können wir jeden gewünschten Bruch auf einfachere Weise ausdrücken, solange er nicht irreduzibel ist. Bei den wissenschaftlichen Taschenrechnern von Casio (der unter Studenten am häufigsten verwendeten Marke) müssen wir die Taste drücken, die mit dem folgenden Ausdruck „S⇔D“ gekennzeichnet ist. Dadurch können wir Ausdrücke aller Art , einschließlich Brüche, vereinfachen. Bei anderen Marken gibt es auch Möglichkeiten, dies zu tun. Sie müssen dies jedoch im Handbuch Ihres Modells nachlesen, da die Vorgehensweise ein wenig variieren kann.

Aufgaben zur Vereinfachung von Brüchen gelöst
Hier finden Sie einige Übungen zur Vereinfachung von Brüchen, mit denen Sie die verschiedenen von uns erläuterten Methoden üben können. Wir empfehlen Ihnen, den theoretischen Teil mit der gleichen Bedeutung wie den praktischen Teil zu belegen, da Sie dadurch die mathematischen Konzepte dieser Art von Übung perfekt verstehen.
Übung 1
Vereinfachen Sie die folgenden Brüche, bis Sie den irreduziblen Bruch finden:
Im folgenden Bild finden Sie vier Brüche, die mit einer von drei Methoden vereinfacht wurden. Wenn Sie versuchen, sie auf eigene Faust zu reduzieren, können Sie dies zwar mit der von Ihnen bevorzugten Methode tun, wichtig ist jedoch, dass Sie das richtige Ergebnis erhalten, das Sie mit dem Ergebnis vergleichen sollten, das wir Ihnen in der Korrektur zeigen:

Übung 2
Berechnen Sie den Wert von x in den folgenden Bruchgleichungen:
Wir stellen nun zwei Gleichungen mit Brüchen bereit, die durch Vereinfachung gelöst werden können. Dies ist eine etwas kompliziertere Übung, aber wenn Sie einige grundlegende mathematische Konzepte zusätzlich zu den in diesem Artikel erläuterten anwenden, können Sie sie leicht lösen.
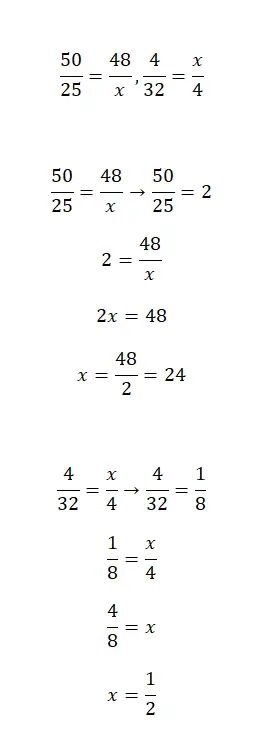
Übung 3
Berechnen Sie die äquivalenten irreduziblen Brüche jedes der unten aufgeführten Brüche:
Jetzt fordern wir Sie heraus, diese Brüche so weit wie möglich zu vereinfachen. Während Sie sie lösen, werden Sie feststellen, dass sie etwas schwieriger sind als die vorherigen. Da einer ein negatives Vorzeichen enthält, ein anderer große Zahlenwerte und ein anderer Potenzen enthält.

Wenn Sie weitere Übungen zu Brüchen wünschen, empfehlen wir Ihnen, diesen letzten Link einzugeben. Dort finden Sie viele Aufgaben und Operationen mit Brüchen. Damit können Sie alle Konzepte im Zusammenhang mit Brüchen üben.