Brüche oder gemischte Zahlen sind ein sehr wichtiges mathematisches Konzept auf dem Gebiet der Analysis. Daher ist es wichtig zu wissen, wie sie funktionieren und wie man Bruchübungen löst. Dies ist das Ziel dieses Artikels, egal ob Sie lernen, Operationen mit Brüchen zu lösen oder jede andere Art von Übung oder Problem, das Zahlen dieses Stils beinhaltet. Beginnen wir jedoch mit den ersten Übungen.
Übung zu Operationen mit Brüchen
Um zu beginnen, bieten wir einige grundlegende Operationen an, die Brüche einbeziehen. Sie müssen sie nur lösen und das vereinfachte Ergebnis ausdrücken. Wenn Sie also mit der Lösung der Berechnungen fertig sind, empfehlen wir Ihnen, die Ergebnisse zu vergleichen und sich die Korrektur anzusehen, die wir Ihnen anbieten. Sie können Ihre Ergebnisse aber auch mit unserem Online- Bruchrechner überprüfen.
Brüche mit gemeinsamem Nenner addieren und subtrahieren
Nachfolgend haben Sie zwei Additionen und zwei Subtraktionen von Brüchen gelöst. Versuchen Sie, sie selbst zu lösen, und vergleichen Sie das Ergebnis. Auf diese Weise überprüfen Sie die Lösungsmechanismen für diese Art von Vorgang:
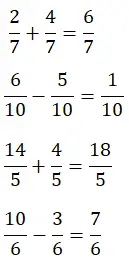
Brüche mit unterschiedlichen Nennern addieren und subtrahieren
Jetzt heben wir das Niveau etwas an, denn um die Addition und Subtraktion von Brüchen mit unterschiedlichen Nennern zu lösen, müssen wir zunächst den lcm der Nenner ermitteln. Die Berechnung wird daher etwas komplizierter.
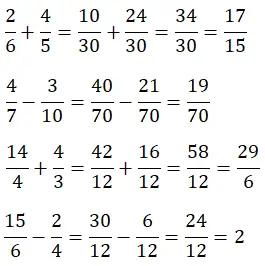
Brüche multiplizieren und dividieren
In diesem Abschnitt müssen Sie die Multiplikation und Division von Brüchen lösen. Diese Operationen sind sehr einfach durchzuführen, müssen aber noch geübt werden. Wie in den beiden vorherigen Abschnitten haben Sie zwei von jedem Typ.
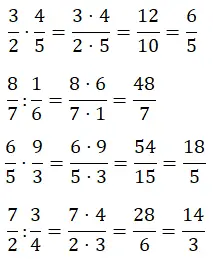
kombinierte Brüche
Schließlich müssen Sie kombinierte Brüche lösen, bei denen es sich um mit Brüchen kombinierte Operationen handelt. Der komplizierteste Teil davon ist die Berechnung, da Sie alle Kenntnisse über Operationen mit gemischten Zahlen sammeln müssen, um eine solche Berechnung korrekt lösen zu können.

Übung zur Umrechnung von Dezimalzahlen und Brüchen
Sie sollten nun versuchen, die folgenden Dezimalzahlen in einen erzeugenden Bruch umzuwandeln und umgekehrt. Um es richtig zu machen, müssen Sie jedoch die Art der Dezimalzahl (exakt, rein periodisch oder gemischt periodisch) berücksichtigen, da die Konvertierungsmethoden variieren. Wenn Sie sich nicht an diese Methoden erinnern, empfehlen wir Ihnen, unseren Artikel über Brüche zu lesen, denn dort erklären wir Ihnen alle Vorgehensweisen zur Umrechnung zwischen Dezimalzahlen und Brüchen und umgekehrt. Nachfolgend finden Sie einige gelöste Konvertierungen. Wir empfehlen Ihnen, diese selbst durchzuführen:

Übung zu äquivalenten Brüchen
Nachdem Sie die Grundrechenarten und Umrechnungen geübt haben, ist es an der Zeit, mit äquivalenten Brüchen zu beginnen. In diesem Abschnitt zeigen wir Ihnen mehrere Brüche und Sie müssen die Paare äquivalenter Brüche finden. Auf diese Weise üben Sie das Konzept der Äquivalenz und wiederholen auch die Vereinfachung von Brüchen .

Übung zum Bruchvergleich
Als nächstes zeigen wir Ihnen mehrere Brüche und Sie müssen diese mit den Symbolen „<“, „=“ und „>“ vergleichen. Um diese Aufgabe zu lösen, müssen Sie einen gemeinsamen Nenner finden und beide Brüche in diesen Nenner umrechnen. Auf diese Weise können Sie erkennen, welcher der beiden Zähler größer ist, und müssen entsprechend handeln:

Übung zu Brüchen auf dem Zahlenstrahl
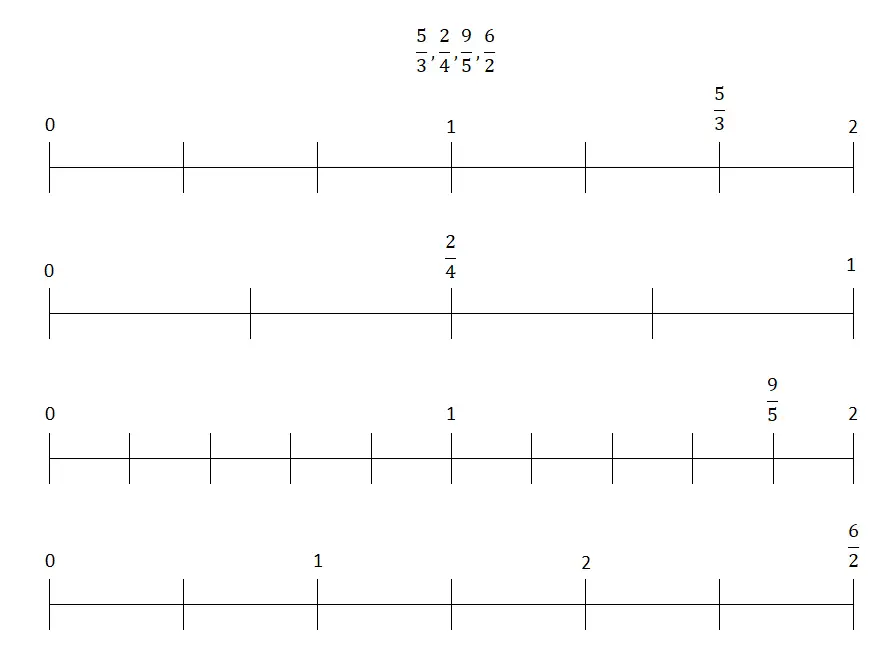
In dieser Übung müssen Sie die verschiedenen Brüche, die wir Ihnen geben werden, auf einer Zahlengeraden anordnen, sodass das Auflösungsverfahren sehr unterschiedlich sein kann. Sie können beispielsweise den Abstand zwischen zwei ganzen Zahlen durch so viele Teile dividieren, wie durch den Wert des Nenners angegeben, und dann den Bruch in das durch den Zähler angegebene Segment einfügen.
Darüber hinaus können Sie den Zähler durch den Nenner dividieren und so eine Dezimalzahl erhalten, die Sie später in die Zeile einfügen. Obwohl dieses zweite Verfahren viel grundlegender ist, haben wir uns aus diesem Grund für die erste von uns erläuterte Methode entschieden. Davon abgesehen sind die Brüche, die Sie auf der rechten Seite platzieren müssen, wie folgt:
Bruchprobleme
Schließlich kommen wir zum letzten Teil dieses Artikels, in dem wir uns mit einigen Bruchproblemen befassen. Zunächst möchten wir jedoch die richtige Vorgehensweise beschreiben, die Sie bei der Lösung mathematischer Probleme anwenden sollten:
- Verstehen Sie das Problem: Der erste Schritt besteht darin, eine gute Lektüre durchzuführen, durch die Sie das gesamte Problem verstehen. Auf diese Weise machen Sie sich mit allen in der Erklärung erläuterten Informationen vertraut. Wenn Sie diesen Teil richtig ausführen, haben Sie viel erreicht, da Sie wissen, wie Sie die Lösung und alle Berechnungen weiterleiten.
- Problemstellung: Sobald Sie wissen, wo das Problem liegt, müssen Sie es darlegen. Sie können dies mithilfe eines Diagramms, einer Zeichnung oder einer kleinen grafischen Darstellung der Daten tun. In diesem Schritt beginnen Sie, darüber nachzudenken, wie Sie die Daten verbinden und das Problem lösen können.
- Lösen Sie das Problem selbst: Später können Sie das Problem weiterhin numerisch lösen. In dieser Phase müssen Sie die Theorien testen, die Sie im vorherigen Abschnitt aufgestellt haben. Hier führen Sie tatsächlich einen Aktionsplan aus und erhalten die Ergebnisse. Sie müssen also sehr konzentriert sein.
- Interpretieren Sie die Lösungen: Wenn Sie schließlich bereits über die Lösungen verfügen, müssen Sie diese Ergebnisse interpretieren und sie im Kontext des Problems verstehen. Dieser letzte Schritt ist sehr wichtig und viele Leute ignorieren ihn, weil sie denken, dass ein numerisches Ergebnis ausreicht, aber in Wirklichkeit muss man die Lösung in einem Satz zusammenfassen.
Problem 1
Wenn wir einen Pool mit einem Wasserhahn füllen möchten, dauert es 6 Stunden, wenn wir es jedoch mit einem anderen Wasserhahn tun, dauert es 8 Stunden. Wie viel Wasser wird in 2 Stunden gefüllt, wenn wir beide Wasserhähne gleichzeitig benutzen? Drücken Sie das Ergebnis als Bruch aus.
Um dieses Problem zu lösen, müssen wir Brüche verwenden. Grundsätzlich berechnen wir separat, wie viel jeder Wasserhahn in diesen zwei Stunden füllt. Der erste Hahn füllt also 1/6 des Tanks in einer Stunde, und wenn wir ihn mit zwei Stunden multiplizieren, werden 2/6 gefüllt. Während das zweite Tippen 1/8 in einer Stunde ausfüllt, müssen wir es auch mit 2 multiplizieren, womit wir 2/8 erhalten.
Abschließend addieren wir die beiden Brüche, um die Gesamtmenge des gefüllten Pools zu erhalten. Also bleiben uns 2/6 + 2/8 = 7/12 des Pools.
Problem 2
Wir haben 64 Bonbons, aber 1/4 davon geben wir unserem Freund Marcos. Dann essen wir 3 Bonbons und geben 2/5 der restlichen Menge unserer Freundin María. Wie viel Süßigkeiten haben wir noch? Drücken Sie es als ganze Zahl aus.
Zuerst müssen wir ein Viertel von der Gesamtmenge von 64 abziehen, dann werden wir 3 vom erhaltenen Ergebnis abziehen und schließlich werden wir zwei Fünftel dieser Menge an Süßigkeiten abziehen. Damit können wir dies mit kombinierten Brüchen berechnen:
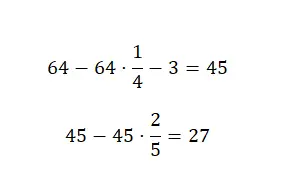
Daher bleiben am Ende 27 Bonbons übrig.
Problem 3
Wir verfügen über ein Grundstück von 10.000 m², das in drei ungleiche Teile aufgeteilt ist. Der erste Abschnitt stellt 3/6 der Gesamtfläche dar und der zweite Abschnitt entspricht der Hälfte des vorherigen. Welcher Bruchteil beschreibt die Fläche des dritten Abschnitts? Wie viele Quadratmeter hat jeder Sektor?
Als erstes berechnen wir den Bruch des dritten Diagramms. Dies geschieht durch eine sehr einfache Subtraktion von Brüchen. Als nächstes berechnen wir die Fläche jedes Abschnitts, indem wir den Bruchteil einer Zahl berechnen. In unserem Fall beträgt dieser Zahlenwert 10.000. Unten sehen Sie den gesamten Vorgang: