Eine quadratische Gleichung oder quadratische Gleichung ist eine Gleichung vom Grad 2, bei der der größte Exponent eines ihrer Terme gleich 2 ist. Das bedeutet, dass die Gleichung bis zu zwei verschiedene Lösungen haben kann, obwohl sie auch eine eindeutige Lösung haben kann oder überhaupt keine.
Um die Lösungen oder Wurzeln quadratischer Gleichungen zu berechnen, können wir zwei verschiedene Verfahren anwenden: mithilfe der quadratischen Formel oder durch Faktorisieren des Ausdrucks . In diesem Artikel sprechen wir über beide Methoden und geben Ihnen einige praktische Übungen. Allerdings werden wir vorher einige Konzepte klären, damit die gesamte Erklärung sehr gut verstanden wird und Sie das Beste aus der Lektüre herausholen.
Arten quadratischer Gleichungen
Die Hauptkategorisierung zwischen quadratischen Gleichungen basiert auf der Struktur des Ausdrucks selbst. Daher ist die Standard- oder übliche Struktur dieser Ausdrücke wie folgt: ax² + bx + c . Diese übliche Form entspricht einer vollständigen Gleichung, aber wenn es Null- oder Nullterme gibt, kann die Struktur variieren, was zu unvollständigen Gleichungen führt. Als nächstes erklären wir die Eigenschaften aller Typen genauer.
Vollständige quadratische Gleichungen
Wie wir bereits sagten, haben wir die vollständigen quadratischen Gleichungen , diese haben alle Koeffizienten a, b und c ungleich Null. Der Ausdruck folgt also buchstabengetreu der Struktur ax² + bx + c, da er alle Terme enthält: den quadratischen Term, den linearen Term und den unabhängigen Term. Ein Beispiel dieser Art ist die folgende Gleichung: x² + 2x + 1 = 0.
Unvollständige quadratische Gleichungen
Unvollständige Gleichungen können wir danach unterscheiden, welcher Koeffizient gleich Null ist. Denken Sie daran: Wenn diese Erklärung Ihre Zweifel nicht ausräumt, finden Sie unten ein Bild, in dem Sie alle Fälle Schritt für Schritt finden.
- Unvollständige Gleichungen (b = 0): In dieser ersten Situation finden wir einen Ausdruck, der der folgenden Struktur folgt: ax² + c = 0. Damit erhalten wir zwei Ergebnisse: das Negative und das Positive der Wurzel des Bruchs c/a .
- Unvollständige Gleichungen (c = 0): Wenn wir die Form ax² + bx = 0 haben, müssen wir die Gleichung faktorisieren, um den Ausdruck x (ax + b) = 0 zu erhalten. Wir werden daher zwei Lösungen haben: x = 0 und x = – b/a.
- Unvollständige Gleichungen (b = c = 0): In diesem Fall haben wir eine Gleichung ax² = 0 und wir haben nur eine mögliche Lösung, nämlich x = 0.
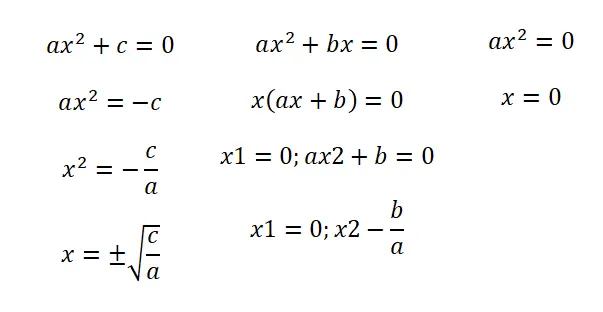
Es ist erwähnenswert, dass Sie mit den Verfahren, die wir Ihnen beigebracht haben, unvollständige Gleichungen schneller lösen können. In allen Fällen können Sie jedoch die quadratische Formel verwenden, die wir Ihnen weiter unten beibringen. Sie müssen lediglich eine Null in die Koeffizienten schreiben, die nicht existieren.
Formel für quadratische Gleichungen
Um quadratische Gleichungen (ax² + bx + c = 0) zu lösen, müssen wir die allgemeine Formel oder die quadratische Formel anwenden und dann die numerischen Werte ersetzen , die jedem Buchstaben im mathematischen Ausdruck entsprechen.
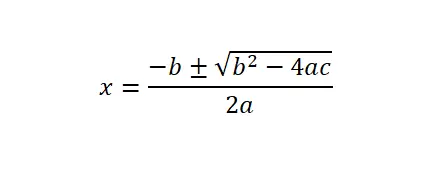
Außerdem ist es wichtig zu erklären, dass die Diskriminante (Δ) der Ausdruck b² – 4ac ist, der unter der Quadratwurzel liegt. Anhand dieses mathematischen Konzepts können wir erkennen, wie viele Lösungen diese quadratische Gleichung hat. Grundsätzlich gibt es drei Möglichkeiten: Die Diskriminante ist negativ (es gibt keine reellen Lösungen), die Diskriminante ist Null (es gibt nur eine Lösung) oder die Diskriminante ist positiv (es gibt zwei Lösungen).
Beispiel einer vollständig gelösten quadratischen Gleichung
Versuchen Sie, die folgende quadratische Gleichung zu lösen: 2x²+4x-6=0 und überprüfen Sie Ihr Ergebnis mit dem folgenden. Wir empfehlen Ihnen, wie folgt vorzugehen: Analysieren Sie den Gleichungstyp (Identifizieren Sie die Nullterme), berechnen Sie die Diskriminante, um die Anzahl der vorhandenen Lösungen zu ermitteln, und lösen Sie schließlich die vorgeschlagene Gleichung mit der Formel.
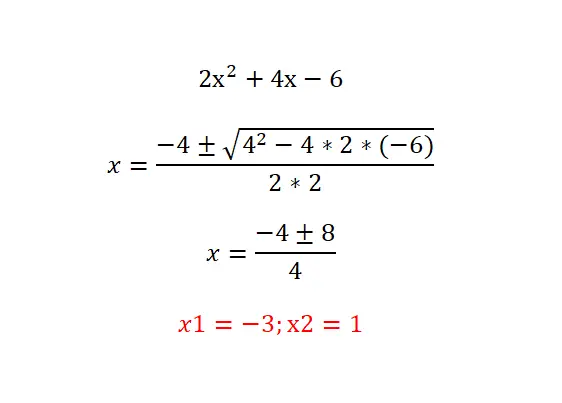
Faktorielle quadratische Gleichungen
Die zweite Methode zur Lösung quadratischer Gleichungen ist die Faktorisierung . Um ein Polynom (in unserem Fall ein quadratisches Polynom) zu faktorisieren , können wir verschiedene Methoden verwenden. Allerdings lassen sich Gleichungen dieses Stils im Allgemeinen durch einen gemeinsamen Term faktorisieren. Und wenn nicht, können Sie versuchen, Notable Identities anzuwenden, aber normalerweise müssen Sie in solchen Situationen keine anderen Methoden kennen.
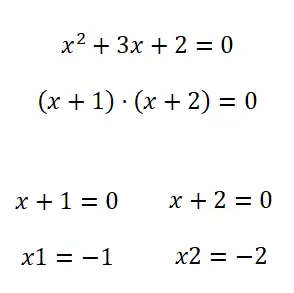
Übungen zu quadratischen Gleichungen mit Lösungen
Nachfolgend finden Sie eine Reihe von Übungen zu vollständigen und unvollständigen quadratischen Gleichungen . Auf diese Weise können Sie die gesamte in diesem Artikel erläuterte Theorie noch einmal durchgehen und es wird Ihnen klarer, wie Sie sie in den Übungen anwenden können. Wir empfehlen, dass Sie versuchen, sie selbst zu lösen, und sich die Lösung erst dann ansehen, wenn Sie sie abgeschlossen haben oder nicht weiterkommen. Das heißt, Sie können jetzt mit dem Lösen der Übungen beginnen.
Übung 1
Lösen Sie die folgende quadratische Gleichung:
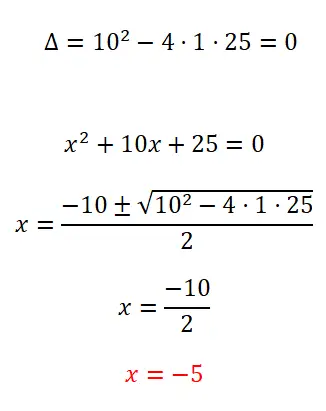
- Wir beginnen mit der Berechnung der Diskriminante, um die Anzahl der möglichen Lösungen zu ermitteln.
- Da es sich um eine vollständige quadratische Gleichung handelt, wenden wir die quadratische Formel an und lösen die Berechnungen.
- Wir erhalten den Wert des unbekannten x.
Übung 2
Lösen Sie die folgende quadratische Gleichung:
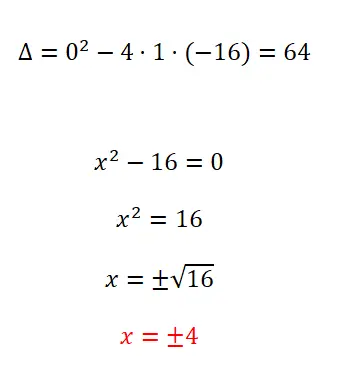
- Wir beginnen mit der Berechnung der Diskriminante.
- Da wir eine unvollständige quadratische Gleichung haben, in der b = 0 ist, wenden wir für Gleichungen dieser Art den Standard an.
- Wir lösen die Rechnung, um das Ergebnis zu erhalten, und dürfen das ±-Zeichen nicht vergessen.
Übung 3
Lösen Sie die folgende ungeordnete quadratische Gleichung:
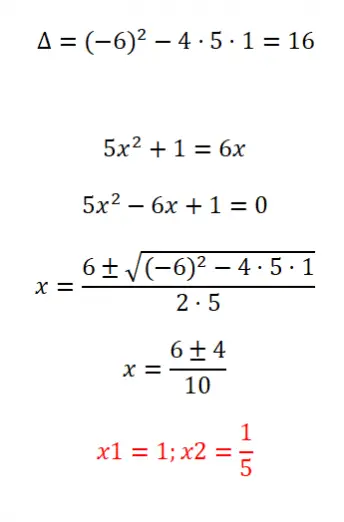
- Wir beginnen mit der Berechnung der Diskriminante der Gleichung.
- Bevor wir die Formel anwenden können, müssen wir die Gleichung gemäß der Struktur ax² + bx + c = 0 ordnen.
- Dann wenden wir die allgemeine Formel an.
- Und schließlich erhalten wir die Ergebnisse.
Übung 4
Lösen Sie die folgende quadratische Gleichung durch Faktorisieren:
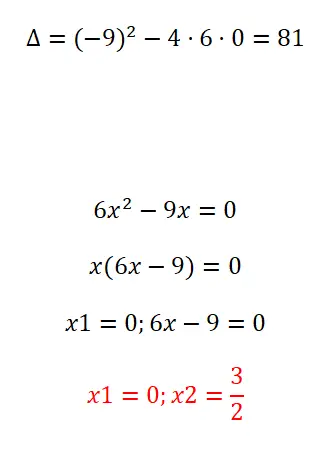
- Wir berechnen zunächst die Diskriminante.
- Als nächstes extrahieren wir den gemeinsamen Faktor von x.
- Die erste Lösung ist also x = 0.
- Und das zweite ist x = 3/2.
Übung 5
Lösen Sie die vollständige quadratische Gleichung, die wir unten zeigen:
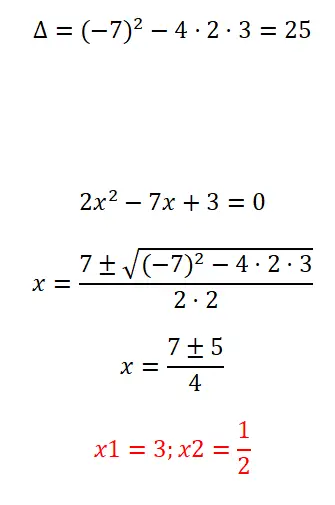
- Wie immer berechnen wir die Diskriminante, um herauszufinden, wie viele Lösungen die betreffende Gleichung hat.
- Als nächstes wenden wir die quadratische Formel an, da es sich um eine vollständige Gleichung handelt.
- Abschließend drücken wir das Ergebnis der Gleichung aus.
Übung 6
Lösen Sie die von uns angebotene quadratische Gleichung mit Brüchen:
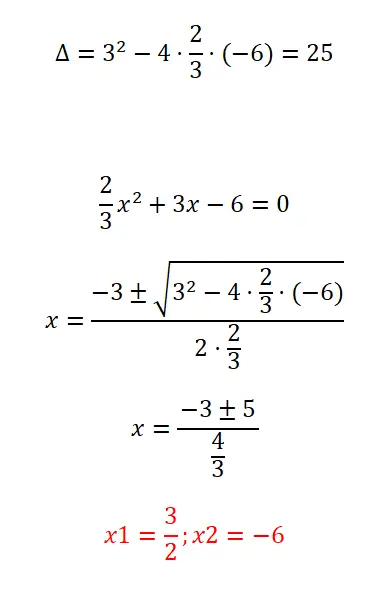
- Wir beginnen mit der Berechnung der Diskriminante des Ausdrucks.
- Als nächstes wenden wir die quadratische Formel an und berücksichtigen dabei, dass der Koeffizient „a“ durch einen Bruch gebildet wird.
- Wir lösen die Rechnung.
- Und wir haben bereits die beiden Wurzeln der Gleichung.
Übung 7
Lösen Sie die folgende quadratische Gleichung:
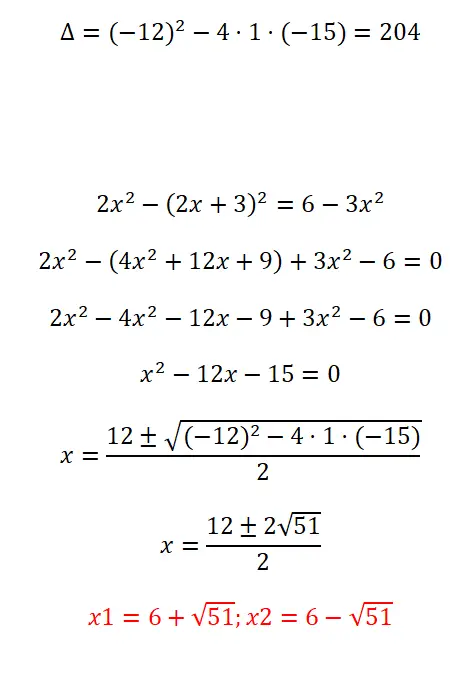
- Wir beginnen mit der Berechnung der Diskriminante.
- Bevor wir die Formel anwenden, müssen wir den Ausdruck vereinfachen und ihm die Form ax² + b + c = 0 geben.
- Wir ersetzen alle Koeffizienten in der Formel und lösen die Berechnung.
- Endlich erhalten wir das Ergebnis.
Übung 8
Beweis für die Lösung der folgenden quadratischen Gleichung:
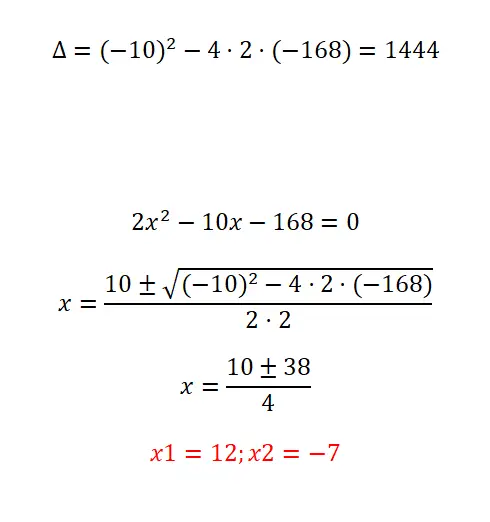
- Wir beginnen mit der Berechnung der Diskriminante.
- Wie Sie sehen, handelt es sich um eine einfache quadratische Gleichung, obwohl sie recht große Koeffizienten hat. Daher müssen wir die Formel anwenden und bei der Durchführung der Operationen vorsichtig sein.
- Am Ende erhalten wir beide möglichen Lösungen.