Ein Dreiersatz ermöglicht es uns, die Proportionalitätsbeziehungen zu kennen, die zwischen bestimmten Werten bestehen. Aus diesem Grund wenden wir es fast täglich in allen Bereichen des täglichen Lebens an. Um ein Beispiel zu nennen: Berechnen Sie Prozentsätze , führen Sie Umrechnungen zwischen Einheiten (Masse, Volumen, Zeit usw.) durch und führen Sie im Allgemeinen Berechnungen auf der Grundlage von Äquivalenzen durch. Diese letzte Anwendung ermöglicht es uns, diese mathematische Ressource in fast jedem Fach zu nutzen.
Wenn Sie also lernen möchten, wie Sie die Dreierregeln lösen , empfehlen wir Ihnen, bis zum Ende des Artikels zu bleiben. Darin erklären wir, wie man sie löst, welche Typen es gibt, welche Anwendungen sie haben und Sie finden sogar einige gelöste Beispiele. Kurz gesagt: Wenn Sie diesen Artikel zu Ende gelesen haben, wissen Sie alles, was Sie über dieses mathematische Konzept wissen müssen.
Dreiregelrechner
Mit diesen Regeln von drei Rechnern (der erste ist die direkte Proportionalität und der zweite ist die indirekte Proportionalität) können Sie alle Ihre Übungen überprüfen und korrigieren. Die Bedienung ist sehr einfach, Sie müssen lediglich die Ihnen bekannten Daten in drei der vier Felder eingeben und wenn Sie auf die Schaltfläche „Berechnen“ klicken, wird der Wert von x angezeigt. Aber machen Sie sich keine Sorgen, wenn Sie noch nicht wissen, wie Sie eine solche Berechnung strukturieren sollen, denn im nächsten Abschnitt erklären wir Ihnen das ausführlich.
Direkter Dreisatzrechner
Rechner zur Umkehrung der Dreierregel
Wie erstellt man eine Dreierregel?
Um eine Dreierregel zu lösen, müssen Sie zunächst herausfinden, welche Sie verwenden möchten: die direkte Dreierregel oder die indirekte Dreierregel. Wir müssen auch unterscheiden, welche Art von Verhältnismäßigkeit wir verwenden werden: einfache Dreierregel oder zusammengesetzte Dreierregel. Da jeder über eine dieser Optionen verfügt, hat er eine andere Art der Datenorganisation und eine andere Formel . Um also zu wissen, wann Sie die einzelnen Typen auswählen sollten, empfehlen wir Ihnen, die folgende Erklärung zum Lösen einer Dreierregel zu lesen.
1. Identifizieren Sie die Beziehungen zwischen den verschiedenen Variablen
Der erste Schritt zur Lösung eines Dreiersatzes besteht darin, eine Art Diagramm oder eine Beziehung zwischen den Variablen zu erstellen. Im Allgemeinen erfolgt dies normalerweise mit dem typischen Diagramm, das im Bild unten zu sehen ist. Dadurch haben wir eine klarere Struktur der Berechnung und können später die Berechnungen durchführen. Sie müssen nur die Buchstaben A, B und C durch die entsprechenden Werte ersetzen : In der linken Spalte stehen die numerischen Werte der Größe, die Sie als Ganzes kennen (beide Werte), und in der rechten Spalte stehen die Werte von der Größe, die das Unbekannte hat. Sie müssen auch die Linien respektieren, daher muss A der Betragswert auf der linken Seite sein, der sich auf die Variable B bezieht.
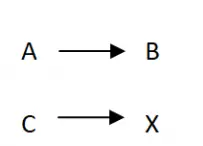
2. Stellen Sie die Verhältnismäßigkeit eines Dreiersatzes fest
Der nächste Schritt besteht darin, die Proportionalität zwischen den Variablen zu ermitteln . Dazu analysieren wir die Änderung des numerischen Werts zwischen den Variablen jeder Größe. Wenn wir am Ende eine gerade Dreierregel erhalten, dann wird, wenn eine der Größen zunimmt, auch die andere zunehmen. Aber wenn wir am Ende zu einer umgekehrten Dreierregel kommen, wenn eine Größe zunimmt, nimmt die andere ab. Dies ist wichtig zu beachten, da die Formel von Fall zu Fall unterschiedlich sein kann.
3. Einfache oder aus drei Regeln bestehende Regeln
Abschließend werden wir die Dreierregeln in zwei Typen unterscheiden, abhängig von der Anzahl der Variablen, die wir mithilfe der Proportionalität in Beziehung setzen. Beim einfachen Dreiersatz erhalten wir den Wert der Variablen X aus der Proportionalität einer anderen Größe. Während die Dreierregel es uns ermöglicht, die Variable X basierend auf der Proportionalität von zwei oder mehr Größen zu berechnen. Als nächstes zeigen wir Ihnen die Formeln und die grafische Darstellung dieser beiden Konzepte, damit kein Zweifel daran besteht:

Beispiel für eine einfache Dreierregel
Wenn zehn Bücher fünfzig Euro kosten, wie viel Geld werden wir dann ausgeben, wenn wir 20 Bücher kaufen?
Um das Ergebnis zu erhalten, müssen wir eine einfache und unkomplizierte Dreierregel lösen. Wir verwenden daher die Formel X = (B · C) / A:
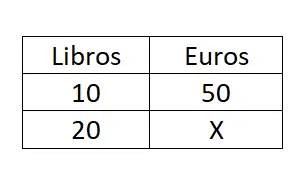
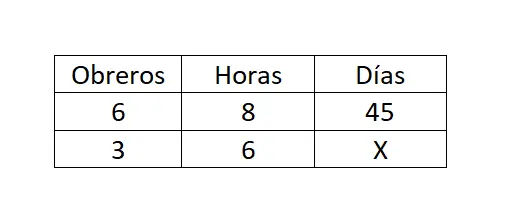
Beispiel einer Dreierregel
Wenn 6 Arbeiter, die 8 Stunden am Tag arbeiten, in 45 Tagen ein Haus bauen, wie viele Tage brauchen dann 3 Arbeiter, die 6 Stunden am Tag arbeiten, um den gleichen Bau fertigzustellen?
In diesem Fall haben wir eine zusammengesetzte und indirekte Dreierregel. Daher verwenden wir die Formel X = (A 1 · B 1 · C 1 ) / (A 2 · B 2 ):
Anwendungen der Dreierregel
Wie wir in der Einleitung erwähnt haben, ermöglichen uns die Dreierregeln, viele Dinge zu berechnen und wenden sie daher in jedem Bereich des täglichen Lebens an. Obwohl diese Art von Anwendungen ein gemeinsames Merkmal aufweist, ist es, dass sie anhand von Proportionen berechnet werden. Um ein paar Beispiele zu nennen:
- Prozente berechnen
- Umrechnungen zwischen Einheiten
- Medikamentendosen berechnen
- Berechnen Sie Provisionen
- Noten berechnen
Und zwar fast alle Operationen, die Äquivalenz oder ähnliches erfordern.
Dreierregel auf dem wissenschaftlichen Taschenrechner
In den gängigsten wissenschaftlichen Taschenrechnern gibt es normalerweise keine Funktion oder Taste, mit der wir Dreiersätze lösen können. Wenn Sie also nicht über einen erweiterten Taschenrechner verfügen, in den Sie personalisierte Funktionen hinzufügen können, werden Sie die Regeln von 3 kaum lösen können. Sie müssen den Vorgang daher separat durchführen (auf einem Blatt Papier oder im Kopf). Führen Sie dann den Berechnungsteil im Taschenrechner durch. Auf den ersten Blick mag es etwas langsam erscheinen, aber wenn Sie üben und sich die Dreierregel im Kopf vorstellen können, werden Sie sie in einer Sekunde lösen können .
Abschließend möchte ich Ihnen sagen, dass wir Ihnen einen Link mit Übungen zum Üben hinterlassen, wenn Sie weitere Regeln für drei Übungen durchgehen möchten. Dennoch hoffen wir, dass Ihnen dieser Artikel und unser Online-Rechner zur Dreierregel dabei geholfen haben, dieses mathematische Konzept besser zu verstehen.