Unten in diesem Artikel finden Sie mehrere gelöste Prozentaufgaben , die alle Schwierigkeitsgrade abdecken. Darüber hinaus decken sie eine Vielzahl von Themen ab, die typischerweise anhand von Prozentsätzen untersucht werden. Dennoch empfehlen wir Ihnen, zu versuchen, die Aufgaben selbst zu lösen, und wenn Sie fertig sind, vergleichen Sie Ihre Ergebnisse mit denen, die wir Ihnen in den gleichen Übungen anbieten. Bevor wir mit den Aktivitäten beginnen, werden wir jedoch ein wenig über die besten Methoden sprechen, die es gibt, um Probleme mit Prozentsätzen zu lösen.
Wie löst man Probleme mit Prozentsätzen?
Um ein Prozentproblem zu lösen, empfehlen wir, das grundlegende Lösungsverfahren für mathematische Probleme zu befolgen. In diesem letzten Link erklären wir im Detail, welche Schritte zu befolgen sind, obwohl wir im Folgenden eine Zusammenfassung erstellen, die sich an der Lösung der Prozentsätze orientiert:
- Das Problem verstehen: In dieser ersten Phase der Lösung müssen wir das Problem nach der Art des Prozentsatzes klassifizieren, den es uns berechnen lässt. Die Haupttypen sind im Allgemeinen: Mehrwertsteuer, Erhöhungsprozentsätze, Kürzungsprozentsätze, Äquivalenzprozentsätze und andere.
- Erstellen Sie ein Diagramm: Sobald wir uns darüber im Klaren sind, mit welcher Art von Problem wir konfrontiert sind, müssen wir mit der grafischen Darstellung des Ziels und der Daten der Übung fortfahren. Wenn Sie jedoch nicht zeichnen möchten, können Sie jederzeit ein Diagramm mit den in die Berechnungen einbezogenen Daten schreiben und diese miteinander in Beziehung setzen.
- Beginnen Sie mit den Berechnungen: Später können wir beginnen, die Aufgabe mathematisch zu lösen. Dieser Teil ist einfach, wenn Sie die Aufgabe in den vorherigen Abschnitten richtig angesprochen haben. Seitdem wissen Sie jederzeit genau, was Sie tun müssen, um das Ergebnis zu erzielen.
- Schlussfolgerungen: Schließlich müssen wir das Ergebnis ausdrücken. Dies kann in einem Satz oder einfach in dem Zahlenwert erfolgen, nach dem wir gefragt werden. Und es wird dringend empfohlen, dass wir, wenn wir mit dem Problem fertig sind, es von Anfang bis Ende analysieren und daraus Schlussfolgerungen ziehen.
Prozentaufgaben für alle Niveaus
Nachdem wir nun erklärt haben, wie man Übungen mit Prozentsätzen löst, können Sie mit einigen Übungen mit dem Üben beginnen. In der folgenden Liste finden Sie Aufgaben für alle Klassenstufen , von Übungen für diejenigen, die anfangen, mit Prozentsätzen zu arbeiten, bis hin zu einigen ziemlich komplizierten. Selbst wenn Sie über das erforderliche Niveau verfügen, empfehlen wir Ihnen, mit den einfachsten (den ersten) zu beginnen und so weit wie möglich aufzusteigen.
erstes Problem
An einer Schule gibt es 240 Schüler, von denen 160 alle Fächer bestanden haben. Wie viel Prozent der Studierenden haben alle Fächer bestanden?
Wir haben 160 von 240 Studenten, die alle Fächer bestanden haben, also entsprechen 240 100 % und 160 x %. Um herauszufinden, wie viel x wert ist, machen wir einfach eine einfache Dreierregel :
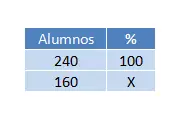
Daher ist das Ergebnis der Operation (160 x 100) ÷ 240 = 66,67 % oder zwei Drittel der Gesamtsumme. Wenn wir also die Lösung in einem Satz ausdrücken wollen, können wir sie mit dem Prozentsatz angeben (das wird in der Aussage von uns verlangt) oder wir können es mit dem Verhältnis tun.
zweites Problem
Auf einem Parkplatz stehen 150 Autos, davon sind 50 % weiß, 30 % rot und der Rest blau. Wie viele Autos gibt es von jeder Farbe?
Wir haben insgesamt 150 Autos und müssen sie anhand der Lackfarbe in drei verschiedene Gruppen einteilen. Wir müssen daher wie zuvor drei Berechnungen durchführen:
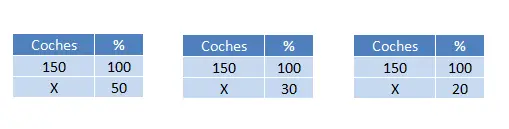
Daher erhalten wir drei Werte: (50 x 150) ÷ 100 = 75 Autos, (30 x 150) ÷ 100 = 45 Autos und (20 x 150) ÷ 100 = 30 Autos. Um schließlich zu überprüfen, ob diese Ergebnisse korrekt sind, können wir sie alle addieren. Das sollte 150 ergeben, denn das ist die Summe. Diese Rechnung ist nicht mehr Teil der Übung, sondern dient der Kontrolle: 75 + 45 + 30 = 150 Autos.
drittes Problem
Wenn wir einen Fernseher kaufen möchten, der 800 € kostet und wir 15 % Rabatt erhalten, wie viel werden wir am Ende für den Fernseher bezahlen?
Wir haben einen Gesamtpreis von 800 €, der um 15 % reduziert wird (dies ist ein Rabattprozentsatz). Wir müssen also nur eine von drei Regeln lösen:
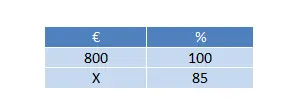
In diesem Fall muss der Wert berechnet werden, der einem Rabattprozentsatz (100 % – 15 %) = 85 % entspricht. Daher bleibt die endgültige Berechnung wie folgt: (85 x 800) ÷ 100 = 680 €.
viertes Problem
Wir hatten 250 Liter in einem Wassertank gespeichert, am ersten Tag war diese Wassermenge auf 75 % der Gesamtkapazität reduziert. Und am nächsten Tag wurde die Restkapazität um 15 % reduziert. Wie viele Kubikmeter verbleiben am Ende des zweiten Tages im Tank?
Um dieses Problem zu lösen, müssen wir zwei Größen in der in der Anweisung festgelegten Reihenfolge berechnen. Wir berechnen zunächst 75 % von 250, dann 85 % (100 % – 15 %) des Restbetrags.
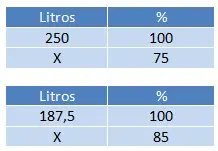
Um die verbleibende Menge vom ersten Tag zu erhalten, lösen wir nach (75 x 250) ÷ 100 = 187,5 Liter Wasser auf und berechnen dann (85 x 187,5) ÷ 100 = 159,375 Liter Wasser.
fünftes Problem
Wenn mir auf zwei Artikel 21 % Mehrwertsteuer berechnet werden, einer für 135 € und der andere für 56 €, das zweite Produkt jedoch von einem Rabatt von 12 % profitiert. Wie viel muss ich am Ende für den Kauf beider Artikel bezahlen?
Bei diesem Problem sind mehrere Berechnungen erforderlich: Wir beginnen mit der Berechnung des Endpreises des zweiten Produkts (nach dem Rabatt), dann berechnen wir den Preis der beiden Produkte inklusive Mehrwertsteuer und schließlich addieren wir die beiden Preise.
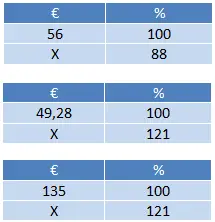
Der Preis des zweiten Produkts, wenn wir den Rabatt anwenden, beträgt (88 x 56) ÷ 100 = 49,28 €. Dann berechnen wir die Mehrwertsteuer auf beide Produkte: (121 x 49,28) ÷ 100 = 59,63 € und (121 x 135) ÷ 100 = € 163,35. Zum Schluss müssen wir nur noch 59,63 + 163,35 = 222,98 € addieren.
letzte Übung
Berechnen Sie die folgenden Prozentsätze:
- 25 % von 540 = 135
- 32 % von 160 = 51,2
- 46 % von 625 = 287,5
- 73 % von 873 = 637,29
Falls Sie diese Übungen abgeschlossen haben und weitere Probleme im Zusammenhang mit Prozentsätzen wünschen, empfehlen wir Ihnen, auf diesen Link zuzugreifen. Dort finden Sie Prozentprobleme im PDF-Format. Diese unterscheiden sich nicht wesentlich von denen, die wir in diesem Artikel angesprochen haben, und sie werden es Ihnen ermöglichen, das Konzept der Prozentsätze zu verinnerlichen.