Berechnen sie das kleinste gemeinsame vielfache (lcm)

Das kleinste gemeinsame Vielfache (LCM) von zwei oder mehr Zahlen ist das kleinste (ungleich Null) Vielfache, das diese Zahlen gemeinsam haben. Es ist die Umkehroperation des größten gemeinsamen Teilers , obwohl sie mit ähnlichen Methoden berechnet wird. Wenn Sie lernen möchten, wie man den LCM berechnet, empfehlen wir Ihnen, weiterzulesen, denn in diesem Artikel erklären wir alle Verfahren (von den einfachsten bis zu den kompliziertesten), um das kleinste gemeinsame Vielfache einer Zahlenmenge zu ermitteln.

lcm-Rechner

Bevor wir darüber sprechen, wie man lcm erhält, möchten wir Sie darüber informieren, dass wir auf dieser Seite einen Rechner für das kleinste gemeinsame Vielfache haben. Damit können Sie die lcm aller gewünschten Zahlen berechnen und so die Ergebnisse Ihrer Übungen vergleichen, um zu sehen, ob Sie sie richtig gelöst haben.

Um den weniger gebräuchlichen Mehrfachrechner zu verwenden, geben Sie durch Komma getrennte ganze Zahlen ein:

lcm berechnen

Wie berechnet man das kleinste gemeinsame Vielfache?

Um das kleinste gemeinsame Vielfache von zwei oder mehr Zahlen zu finden, müssen Sie eine von drei Methoden befolgen, die wir im Folgenden erklären. Als nächstes erklären wir Ihnen detailliert die einzelnen Verfahren, die Sie wählen können, und erklären Ihnen auch, welche Vor- und Nachteile sie haben. Auf diese Weise wissen Sie, welches Sie in der jeweiligen Situation wählen müssen, um das betreffende LCM einfach und schnell zu lösen.

Methode 1: Mehrfachliste

Die erste Methode besteht darin, eine Liste mit Vielfachen der Zahlen zu erstellen, die Sie im LCM berechnen möchten. Dann müssen Sie den kleinsten Wert finden, der sich in allen Listen wiederholt . Auf diese Weise erhalten Sie das kleinste gemeinsame Vielfache. Dann sehen wir es anhand eines Beispiels: lcm (5, 6).

Methode 2: Faktorielle Zerlegung

Zweitens können wir uns dafür entscheiden, die Zahlen zu faktorisieren. Genauer gesagt erleichtert diese Methode die Berechnung des pcm großer Zahlen . Da das Befolgen von Methode 1 bei der LCM großer Zahlen langsam und mühsam sein kann, einfach weil wir sehr lange Listen mit Vielfachen schreiben müssen. Dieses zweite Verfahren kann zunächst etwas komplizierter zu verstehen sein, aber wenn man die Mechanik versteht, hat es viele Vorteile im Vergleich zum vorherigen. Sehen wir uns nun die Vorgehensweise an:

• Faktorielle Zerlegung: Der erste Schritt besteht darin, alle Zahlen, die wir in das LCM aufnehmen werden, in Primfaktoren zu zerlegen. Falls Sie nicht wissen , wie man eine Zahl faktoriell zerlegt , empfehlen wir Ihnen, diesen letzten Link einzugeben. Dort finden Sie eine erstklassige Erklärung, wie Sie Zahlen schnell und effizient vereinfachen können.
• Erstellen Sie einen einzelnen mathematischen Ausdruck: Wenn wir alle Zahlen als Primfaktoren ausgedrückt haben, wählen wir die gemeinsamen und nicht-gemeinsamen Zahlen, erhöht auf den größten Exponenten. Dann schreiben Sie sie als einen einzigen mathematischen Ausdruck auf und lösen schließlich die notwendigen Multiplikationen und/oder Potenzen. Und schon haben Sie den Zahlenwert lcm.

Methode 3: Mathematische Formel

Es gibt eine letzte Möglichkeit, das kleinste gemeinsame Vielfache zu erhalten, die darin besteht, den GCD und die folgende mathematische Formel zu verwenden:

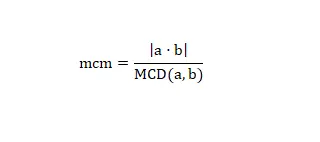
Mit dieser Formel können wir den lcm einer beliebigen Zahl berechnen. Sehen wir uns ein reales Beispiel an: Wenn wir lcm (2,6) berechnen wollen, müssen wir lediglich die Operation (2 x 6) / 2 = 6 lösen. Und wir haben die Berechnung bereits gelöst, wie Sie sehen, ist es eine einfache Methode und schnell , wenn Sie den GCD haben oder ihn leicht berechnen können.

Tipps zur schnellen Berechnung von lcm

Wenn Sie die drei gerade erläuterten Methoden beherrschen, empfehlen wir Ihnen, die Eigenschaften des kleinsten gemeinsamen Vielfachen zu lesen, über die wir jetzt sprechen werden. Denn dank ihnen können Sie einige spezifische Situationen identifizieren, in denen das LCM sehr schnell berechnet werden kann, ohne die bereits erläuterten Strategien anwenden zu müssen.

• Erste durch die zweite teilbare Zahl: Wenn wir das kleinste gemeinsame Vielfache von a und b berechnen wollen, wenn a durch b teilbar ist, dann ist der ppcm dieser beiden Zahlen der größte (in diesem Fall b). Wenn Sie beispielsweise den lcm von 2 und 8 berechnen möchten, ist das Ergebnis das größte, also 8.
• Zwei Primzahlen: Um zwei Primzahlen zu finden, besteht die schnellste Methode darin, sie miteinander zu multiplizieren. Das Ergebnis ist der ppcm. Dies ist logisch, da ihr größter gemeinsamer Teiler 1 ist, was bedeutet, dass wir die Zahl nicht in einfachere Faktoren als die Zahl selbst zerlegen können und sie daher nur miteinander multiplizieren können. Beispielsweise ist der LCM von 3 und 5 das Ergebnis ihres Produkts: 3 x 5 = 15.

Wie erhält man das kleinste gemeinsame Vielfache in Brüchen?

Wenn wir eine Addition oder Subtraktion von Brüchen lösen wollen, müssen wir den kleinsten gemeinsamen Nenner berechnen, der mit lcm identisch ist, jedoch auf Brüche angewendet wird. Im Grunde suchen wir nach dem lcm der beiden Nenner, um dann die Summe als einen einzigen Bruch ausdrücken zu können. Wenn Sie sehen möchten, wie der kleinste gemeinsame Nenner auf die Berechnung eines reellen Bruchs angewendet wird, können Sie diesen Link eingeben.

Lcm auf dem wissenschaftlichen Taschenrechner

Mit der LCM-Taste, die auf jedem wissenschaftlichen Taschenrechner zu finden ist, können Sie das kleinste gemeinsame Vielfache zweier Ganzzahlen berechnen. Im Fall von Casio-Rechnern müssen Sie folgende Syntax bzw. Vorgehensweise befolgen. Zuerst drücken Sie APHA + MCM (diese letzte Taste wird braun beschriftet). Sobald dies erledigt ist, können Sie beide Zahlen eingeben. Beachten Sie jedoch, dass Sie diese durch ein Komma trennen müssen ( UMSCHALT + , ). Abschließend erhalten Sie das kleinste gemeinsame Vielfache, indem Sie auf die Schaltfläche „Gleich“ klicken.

LCM-Übungen Schritt für Schritt gelöst

Als nächstes zeigen wir Ihnen drei Beispiele für die Schritt-für-Schritt-Lösung des kleinsten gemeinsamen Vielfachen . Auf diese Weise können Sie versuchen, diese Probleme zu lösen und ein wenig von dem zu üben, was wir in diesem Artikel erklärt haben. Um die Konzepte zu verinnerlichen, ist es wichtig, dass Sie versuchen, die Übungen zu lösen, denn es ist notwendig, die Theorie auf die Realität anzuwenden. Wir lassen Sie jedoch mit den folgenden Übungen üben:

Berechnen Sie die lcm von 4 und 6

Berechnen Sie die lcm von 6 und 9

Berechnen Sie die lcm von 30 und 40