Was ist Polynomfaktorisierung? Es handelt sich um eine mathematische Technik, mit der Sie ein Polynom in einfachere Faktoren oder Ausdrücke zerlegen können. Und dank dieser Vereinfachung können wir Operationen zwischen mehreren algebraischen Ausdrücken einfacher und komfortabler durchführen. Daher werden wir in diesem Artikel verschiedene Methoden zur Faktorisierung von Polynomen und alle möglichen Fälle der Faktorisierung diskutieren.
Wie faktorisiert man ein Polynom?
Es gibt viele Faktorisierungsmethoden , die ihre eigene Lösungsstruktur haben, aber letztlich auf dem Gleichen beruhen. Darüber hinaus gibt es auch eine Vielzahl von Fällen bezüglich der Polynomkonfiguration. Aus diesem Grund werden wir in den folgenden Abschnitten alle vorhandenen Verfahren und den Zeitpunkt ihrer Verwendung besprechen. Abschließend wenden wir es auf ein reales Beispiel an, damit Sie sich die Konzepte vollständig aneignen können.
Faktorisieren Sie ein Polynom mit der Ruffini-Regel
Die am häufigsten verwendete Methode zur Faktorisierung von Polynomen ist die Ruffini-Regel , da sie einfach anzuwenden ist und das Ergebnis schnell gefunden werden kann. Normalerweise wird diese Technik verwendet, um Polynome mit einem Grad größer als zwei zu faktorisieren, oder manchmal sogar, um Polynome mit einem zweiten Grad zu faktorisieren. Da es Ihnen ermöglicht , die Wurzeln dieses Polynoms sehr grafisch zu ermitteln . Diese Verwendung wird jedoch im nächsten Abschnitt erläutert, der sich auf die Wurzeln eines mathematischen Ausdrucks dieser Art konzentriert.
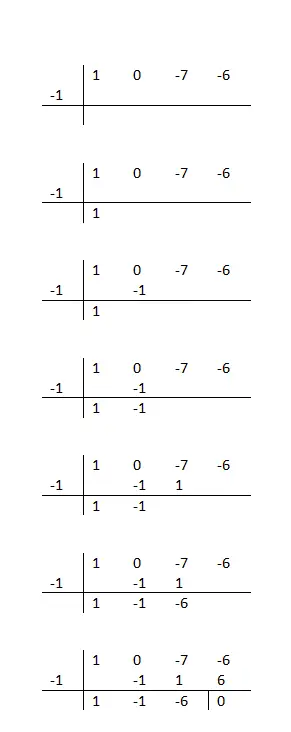
Wie faktorisiert man Polynome mit Ruffini?
Grundsätzlich müssen wir die Koeffizienten des Dividenden in eine horizontale Linie und den Wert einer möglichen Wurzel des Polynoms in die Seite schreiben . Wir sagen „möglich“, weil wir nach einem Teiler suchen müssen, der es uns ermöglicht, einen Rest gleich Null zu erhalten. Andernfalls ist diese Nummer kein gültiger Root und Sie müssen es weiter versuchen.
Als Tipp empfehlen wir, nur die Teilerzahlen des unabhängigen Termes (letzter Wert der horizontalen Linie) auszuprobieren. Um also zu wissen, ob die von Ihnen gewählte Zahl richtig ist, müssen Sie nur die folgende Berechnungssequenz befolgen:
Sie verringern den Koeffizienten, multiplizieren ihn mit der Wurzel, die Sie testen, schreiben ihn unter den nächsten Koeffizienten und führen eine vertikale Addition durch. Sie müssen diese Schritte nur bis zum Ende wiederholen, und wenn Sie fertig sind, wissen Sie, ob dieser Wert korrekt ist oder nicht. Denn nur Zahlen, die einen Rest von Null ergeben, sind gültig.
Wenn Ihnen das mathematische Verfahren, dem Sie folgen müssen, nicht ganz klar ist, können Sie sich das Beispiel in der Spalte links in diesem Text ansehen. Wir empfehlen außerdem, das folgende Polynom zu faktorisieren: x³ + 2x² – x – 2 (basierend auf dem Beispiel). Und um zu wissen, ob Sie die Übung richtig gelöst haben oder nicht, können Sie Ihr Ergebnis mit diesem vergleichen:
- Überschussausdruck = x² + 3x + 2
- Rest = 0
Wir werden nun kurz die Anwendung von Ruffini bei der Faktorisierung erläutern. Wenn Sie jedoch wissen möchten, wie diese mathematische Ressource im Detail verwendet wird, empfehlen wir Ihnen, auf den letzten Artikel zuzugreifen, den wir verlinkt haben, da dort alles sehr gut erklärt wird. Lassen Sie uns zunächst erklären, wie man Polynome mit der Ruffini-Regel faktorisiert:
- Wir zeichnen das Gitter: Wie wir im Bild oben sehen können, erstellen wir eine Box, in der wir die Ruffini herstellen. Grundsätzlich müssen Sie die Koeffizienten des Ausdrucks horizontal geordnet schreiben und diejenigen, die einen Nullwert haben, auslassen. Am Ende sollten Sie eine Darstellung ähnlich der im Bild haben, jedoch mit den Werten Ihres Polynoms.
- Wir berechnen die Wurzeln: Nachdem wir die Struktur gezeichnet und sichergestellt haben, dass alle Zahlen richtig geschrieben sind, beginnen wir mit der Berechnung der Wurzel. Sie müssen die Wurzeln finden, indem Sie der Berechnungssequenz folgen, über die wir direkt über dieser Liste (mit den Bildern) gesprochen haben.
- Wir drücken die Wurzel in der Form (x – a) aus: Wenn wir alle Wurzeln des Polynoms haben, müssen wir sie in der folgenden Form (x – a) ausdrücken. Wenn wir berücksichtigen, dass a die Werte sind, die wir erhalten haben, wenn wir beispielsweise als Ergebnis x = 2, x = -2 und x = 4 extrahiert haben, erhalten wir (x – 2), (x + 2) und ( x – 4).
- Wir fassen alle Faktoren in einem einzigen Ausdruck zusammen: Wenn wir schließlich bereits alle Wurzeln im richtigen Format ausgedrückt haben, müssen wir sie nur noch in einem einzigen algebraischen Ausdruck zusammenfassen. Wenn wir mit dem vorherigen Beispiel fortfahren, hätten wir ungefähr Folgendes: (x – 2) · (x + 2) · (x – 4).
Faktorisieren Sie ein Polynom mithilfe der Wurzeln eines Polynoms
Wir haben das Wurzelkonzept eines Polynoms in Ruffinis Abschnitt zur Hälfte erklärt. Die genaue Definition wäre jedoch: Die Wurzel eines Polynoms P(x) ist ein numerischer Wert a, so dass P(a) = 0 ist . Es handelt sich also um eine Zahl, die die betreffende Funktion oder das betreffende Polynom aufheben kann. Zusammenfassend könnte man sagen, dass es dazu dient, ein Polynom in ein Produkt von Faktoren zu zerlegen.
Wenn uns zum Beispiel der folgende Ausdruck x² − x − 2 gegeben wird und wir ihn entweder mithilfe der Ruffini-Regel faktorisieren oder indem wir einfach die quadratische Gleichung x² − x − 2 = 0 lösen, erhalten wir zwei x-Werte = -1 und x = 2, wenn wir sie also in das Format (x – a) ändern und zusammensetzen, erhalten wir den folgenden Ausdruck: (x + 1) (x − 2), also das faktorisierte Polynom . Und wir können dies auf Polynome mit einem Grad größer als zwei anwenden, obwohl der Ausdruck aus mehr als einem Term besteht.
Faktorisierung eines Polynoms durch Extraktion gemeinsamer Faktoren
Wenn wir Polynome ohne unabhängigen Term oder Ausdrücke, die in allen Termen einen gemeinsamen Faktor haben, faktorisieren möchten, können wir das Polynom mit dieser Technik vereinfachen. Dabei geht es im Wesentlichen darum , die Verteilungseigenschaft auf den gesamten Ausdruck anzuwenden , den sich wiederholenden gemeinsamen Faktor zu entfernen und ihn durch Multiplikation des gesamten Polynoms hinzuzufügen. Nachfolgend finden Sie ein Beispiel für den ersten Fall, über den wir gesprochen haben (Polynom ohne unabhängigen Term):
2x³ + 10x² – 6x = 2x (x² + 5x – 3)
Doppelte Extraktion des gemeinsamen Faktors
Die Extraktion gemeinsamer Faktoren kann sogar durch die Extraktion komplexerer Faktoren erfolgen, die mehrere Variablen umfassen. Und Sie können sogar Polynome extrahieren, die vom Hauptausdruck selbst abgeleitet sind. Es ist wichtig, keine Grenzen zu setzen, wenn Sie diese Art von Operation durchführen möchten, da das Ziel der Faktorextraktion darin besteht , einen algebraischen Ausdruck so weit wie möglich zu vereinfachen .
Faktorisieren von Polynomen mithilfe bemerkenswerter Identitäten
Bemerkenswerte Produkte können uns dabei helfen, Polynomausdrücke zu faktorisieren, da es sich dabei um eine Art vereinfachte algebraische Ausdrücke handelt. Sie helfen uns daher, direkt von einem langen Polynom zu einer kleinen Formel zu gelangen, die aus wenigen Termen besteht. Es wird daher dringend empfohlen, die Formeln bemerkenswerter Identitäten zu lernen, um schnell erkennen zu können, wann Sie sie verwenden können. Und dadurch sparen wir Zeit bei der Faktorisierung mit Ruffini oder einer der anderen Methoden. Als Nächstes behandeln wir die drei Regeln, die Sie lernen müssen:
- Quadratdifferenz: a² – b² = (a + b) · (a – b)
- Quadrat der Summe: a² + 2ab + b² = (a + b)²
- Subtraktionsquadrat: a² – 2ab + b² = (a – b)²
Faktorisierung von Polynomen durch Gruppierung
In einigen Fällen können wir ein Polynom der Struktur x² – ax – bx + ab finden, das durch Entfernen eines gemeinsamen Faktors vereinfacht werden kann: x (x – a) – b (x – a). Und wenn wir noch einmal den gemeinsamen Faktor nehmen, kann er noch weiter vereinfacht werden: (x – a) · (x – b). Daher wären die Wurzeln dieses Polynoms x = a und x = b. Wie Sie sehen, hat diese Art von algebraischem Ausdruck eine Struktur, die sehr einfach zu faktorisieren und zu verwenden ist.
Übungen zur Polynomfaktorisierung
Abschließend möchten wir Ihnen eine Reihe von Übungen anbieten, mit denen Sie das Faktorisieren von Polynomen üben können. Auf diese Weise können Sie die Theorie, die wir heute erläutert haben, besser verinnerlichen. Sie müssen lediglich die Übungen in Ihrem Notizbuch lösen und dann die Ergebnisse mit denen vergleichen, die wir Ihnen unten anbieten.
- x 4 -1 = (x 2 + 1) (x + 1) (x – 1)
- x 5 + x 4 – x – 1 = (x – 1) (x + 1) 2 (x 2 + 1)
- 9×2 + 30x + 25 = (3x + 5) 2
- x 4 – 3x 3 – 3x 2 + 11x – 6 = (x + 2) (x – 3) (x – 1) 2