Irrationale Funktion oder radikale Funktion -

Auf dieser Seite wird erklärt, was eine irrationale Funktion, auch Radikalfunktion genannt, ist und welche Merkmale diese Art von Funktion aufweist. Sie erfahren außerdem, wie Sie den Bereich radikaler oder irrationaler Funktionen berechnen, und können anhand von Beispielen sehen, wie Sie diese in einem Diagramm darstellen, und üben, indem Sie Schritt für Schritt Übungen und Probleme lösen.

Was ist eine irrationale (oder radikale) Funktion?

Eine irrationale Funktion bedeutet dasselbe wie eine radikale Funktion und daher haben sie eine gemeinsame Definition:

Eine irrationale Funktion , auch Wurzelfunktion genannt, ist eine Funktion, die die unabhängige Variable x unter dem Symbol einer Wurzel hat.

Wie wir bereits wissen, kann das Ergebnis einer Wurzel positiv oder negativ sein. Somit hat die Darstellung einer irrationalen (oder radikalen) Funktion zwei mögliche Kurven:

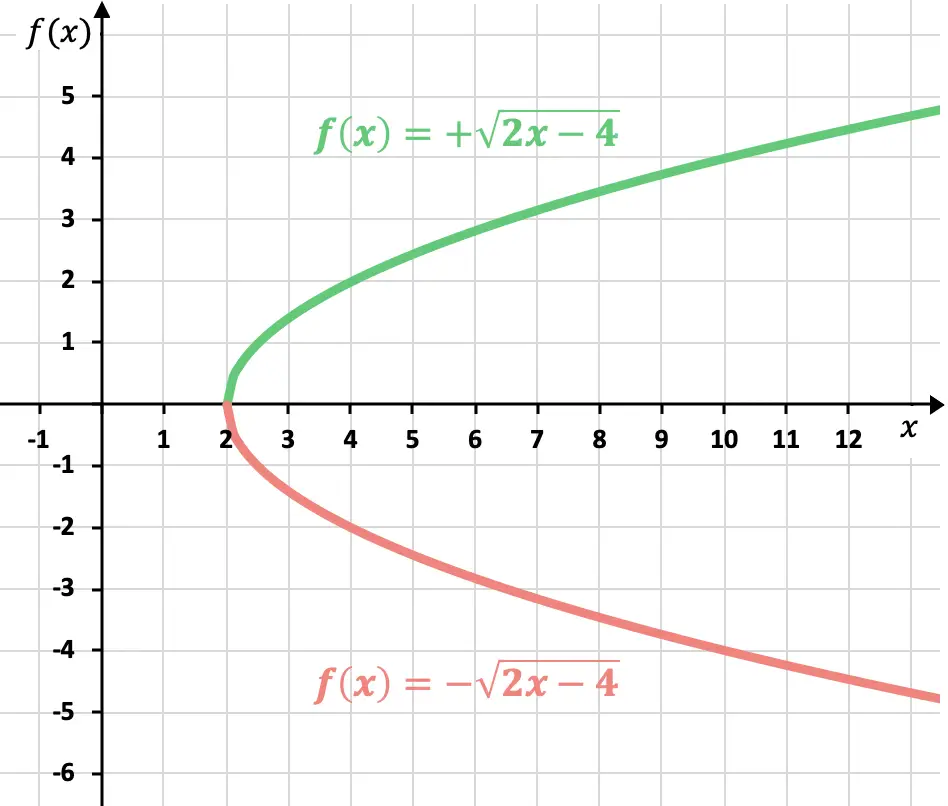
Beispiele für irrationale oder radikale Funktionen

Wenn das Vorzeichen jedoch nicht angegeben ist, soll die positive Funktion dargestellt werden.

Andererseits sollte eine irrationale Funktion nicht mit einer rationalen Funktion verwechselt werden. Obwohl sie sehr ähnliche Namen haben, handelt es sich um zwei völlig unterschiedliche Arten von Funktionen.

Bereich einer irrationalen oder radikalen Funktion

Der Definitionsbereich einer Funktion mit Wurzeln hängt von der Parität des Wurzelindex ab, das heißt, er hängt davon ab, ob der Wurzelindex gerade oder ungerade ist.

Domäne einer Funktion mit Wurzel eines geraden Indexes

Wie Sie wissen, gibt es keine Wurzel (geraden Index) einer negativen Zahl. Daher existiert eine Wurzelfunktion mit geradem Index, solange ihr Inhalt gleich oder größer als 0 ist.

Sehen wir uns als Beispiel an, wie der Definitionsbereich der folgenden radikalen oder irrationalen Funktion berechnet wird:

$f(x)=\sqrt{x-4}$

Dies ist eine radikale gerade Indexfunktion, daher müssen wir uns ansehen, wann ihr Inhalt positiv oder Null ist :

$x-4\ge 0$

Wir lösen die Ungleichung:

$x\ge 4$

Die Funktion existiert also immer dann, wenn x größer oder gleich 4 ist, und wird durch das folgende Intervall angegeben:

$\text{Dom } f= [4,+\infty)$

Domäne einer Funktion mit Wurzel eines ungeraden Index

Bei irrationalen Funktionen mit ungeradem Index tritt dieses Problem nicht auf, da die ungerade Indexwurzel einer negativen Zahl existiert:

$\sqrt[3]{-8}=-2$

Daher gibt es für jeden Wert von x Wurzelfunktionen mit ungeradem Index. Oder anders ausgedrückt: Der Definitionsbereich besteht nur aus reellen Zahlen .

Beispielsweise berechnen wir den Definitionsbereich der folgenden Wurzelfunktion, deren Index ungerade ist:

$f(x)=\sqrt[3]{3x-4}$

Da es sich um eine irrationale Funktion mit ungeradem Index handelt, besteht ihr Definitionsbereich aus reellen Zahlen:

$\text{Dom } f= \mathbb{R}$

Wie man eine irrationale oder radikale Funktion darstellt

Sehen wir uns anhand eines Beispiels an, wie man eine Funktion mit Wurzeln in einem Diagramm darstellt.

Zeichnen Sie die folgende radikale oder irrationale Funktion in ein Diagramm:

$f(x)=\sqrt{x+2}$

Als erstes müssen Sie den Definitionsbereich der Funktion ermitteln. Da es sich um eine Quadratwurzel handelt, muss alles, was darin enthalten ist, positiv sein, da es keine Quadratwurzel einer negativen Zahl gibt. Daher existiert die Wurzelfunktion, solange ihr Inhalt gleich oder größer als 0 ist:

$x+2\ge 0$

$x\ge -2$

Somit besteht der Definitionsbereich der Funktion aus allen Zahlen größer oder gleich -2. Das heißt:

$\text{Dom } f = [-2,+\infty)$

Sobald wir den Definitionsbereich der Funktion kennen, erstellen wir eine Wertetabelle. Je mehr Punkte wir berechnen, desto präziser wird natürlich die Darstellung der Funktion. Aber die Berechnung von 3 oder 4 Punkten im Domänenintervall reicht aus:

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

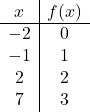
Wir stellen nun die erhaltenen Punkte grafisch dar :

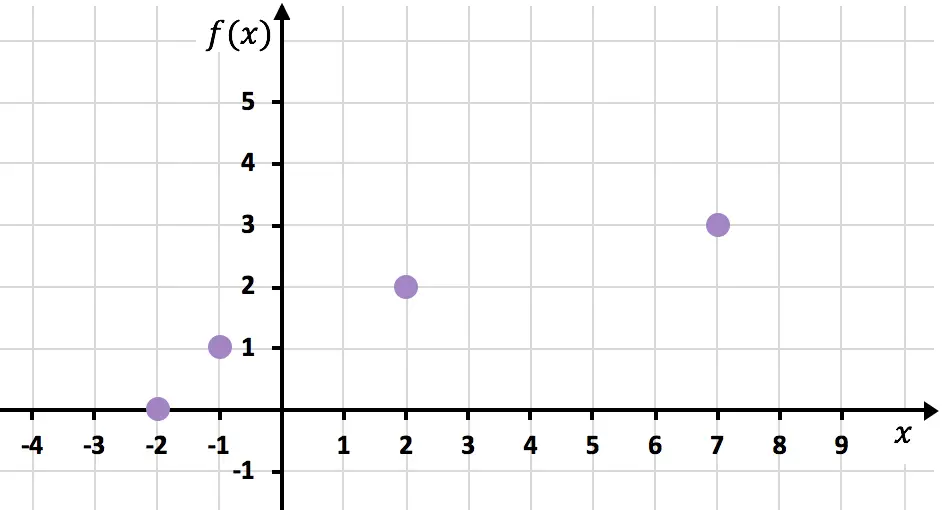
wie man eine radikale oder irrationale Funktion darstellt

Und schließlich verbinden wir die Punkte und verlängern die Kurve, um anzuzeigen, dass die Funktion weiter wächst:

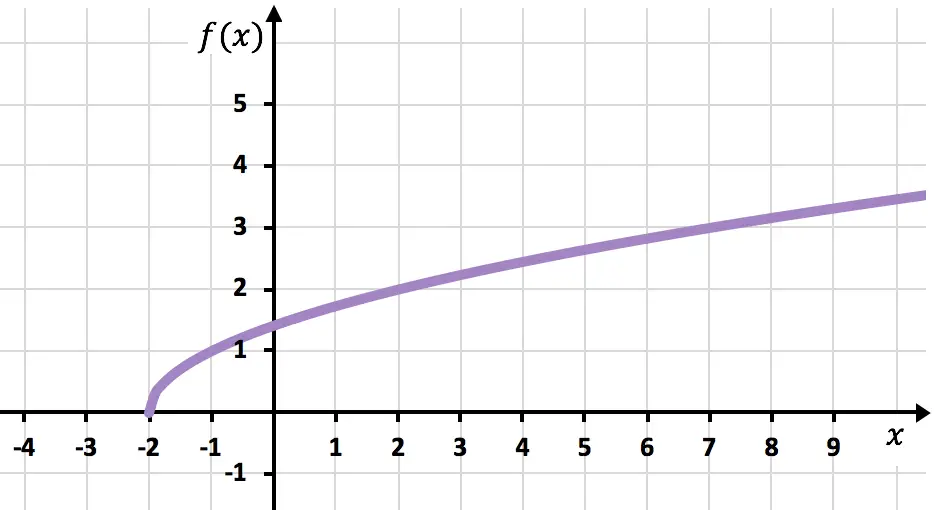
Beispiel einer grafischen Darstellung einer radikalen oder irrationalen Funktion

Gelöste Übungen zu irrationalen oder radikalen Funktionen

Übung 1

Finden Sie den Definitionsbereich der folgenden Wurzelfunktion:

$\sqrt{3x+6}$

Sehen Sie sich die Lösung an

Die Quadratwurzel einer negativen Zahl existiert nicht. Daher existiert die Funktion, wenn das Wurzelargument positiv oder Null ist:

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

Übung 2

Finden Sie den Definitionsbereich der folgenden irrationalen Funktion:

$\sqrt{-x+2}$

Sehen Sie sich die Lösung an

Die Quadratwurzel einer negativen Zahl hat keine reelle Lösung. Daher existiert die Funktion, solange der Inhalt der Wurzel positiv oder Null ist:

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

Denken Sie daran, dass wir, wenn wir in einer Ungleichung die Seiten einer negativen Zahl ändern, die multipliziert oder dividiert, auch das Vorzeichen der Ungleichung drehen müssen.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

Übung 3

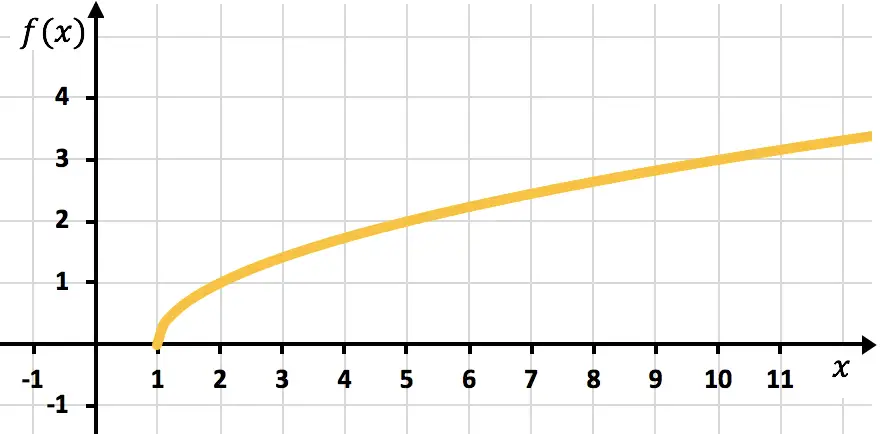
Zeichnen Sie die folgende irrationale Funktion in ein Diagramm:

$f(x)= \sqrt{x-1}$

Sehen Sie sich die Lösung an

Zunächst müssen wir den Definitionsbereich der Funktion berechnen:

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

Jetzt erstellen wir ein Wertearray, indem wir die Werte der Funktion im Domänenbereich angeben:

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

Zum Schluss zeichnen wir die Punkte ein und zeichnen die Funktion im Diagramm auf:

Übung zur schrittweisen Lösung einer irrationalen oder radikalen Funktion

Übung 4

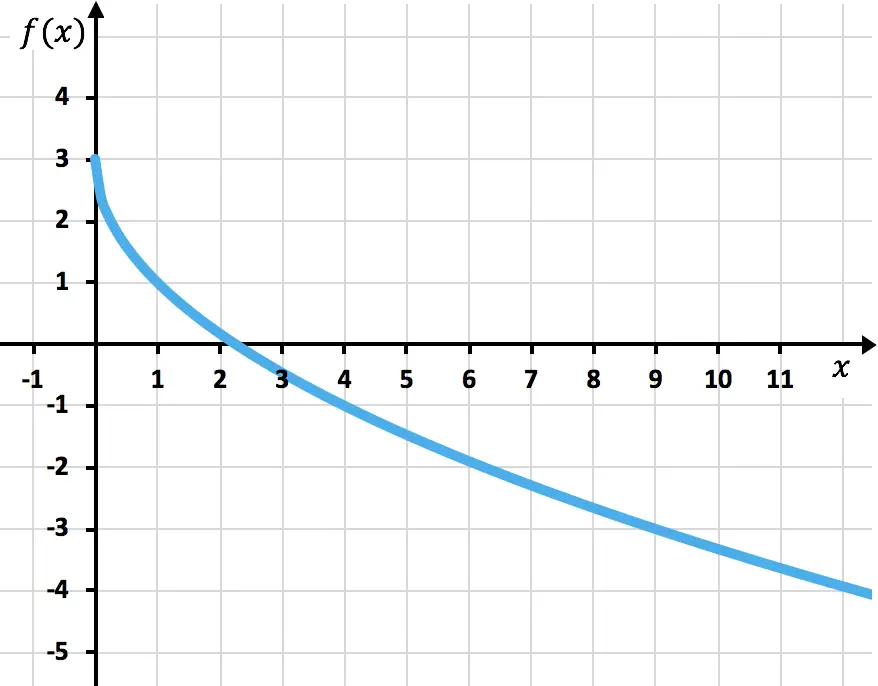
Stellen Sie die folgende irrationale oder radikale Funktion grafisch dar:

$f(x)= -2\sqrt{x}+3$

Sehen Sie sich die Lösung an

Zunächst müssen wir den Definitionsbereich der Funktion berechnen:

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

Jetzt erstellen wir ein Wertearray, indem wir die Werte der Funktion im Domänenbereich angeben:

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

Zum Schluss zeichnen wir die Punkte ein und zeichnen die Funktion in das Diagramm ein:

Übung 5

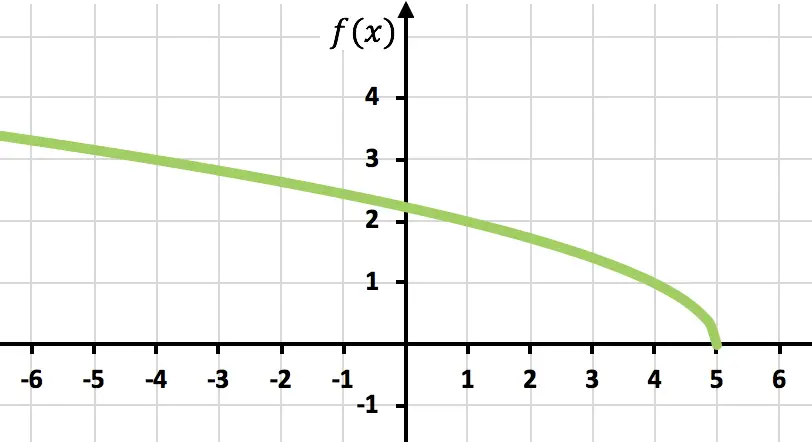
Stellen Sie die folgende irrationale oder radikale Funktion grafisch dar:

$f(x)= \sqrt{-x+5}$

Sehen Sie sich die Lösung an

Bevor wir die Funktion zeichnen, müssen wir den Definitionsbereich der Funktion berechnen:

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

Denken Sie daran, dass wir, wenn wir in einer Ungleichung die Seiten einer negativen Zahl ändern, die multipliziert oder dividiert, auch das Vorzeichen der Ungleichung ändern müssen.

$x\le5$

$\text{Dom } f = (-\infty,5]$

Nun erstellen wir eine Wertetabelle, indem wir die Funktion an Punkten auswerten, die zum Definitionsbereich der Funktion gehören:

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

Und schließlich stellen Sie einfach die Punkte dar und zeichnen die Funktion in das Diagramm ein:

entschlossene Übungen radikaler oder irrationaler Funktionen

Übung 6

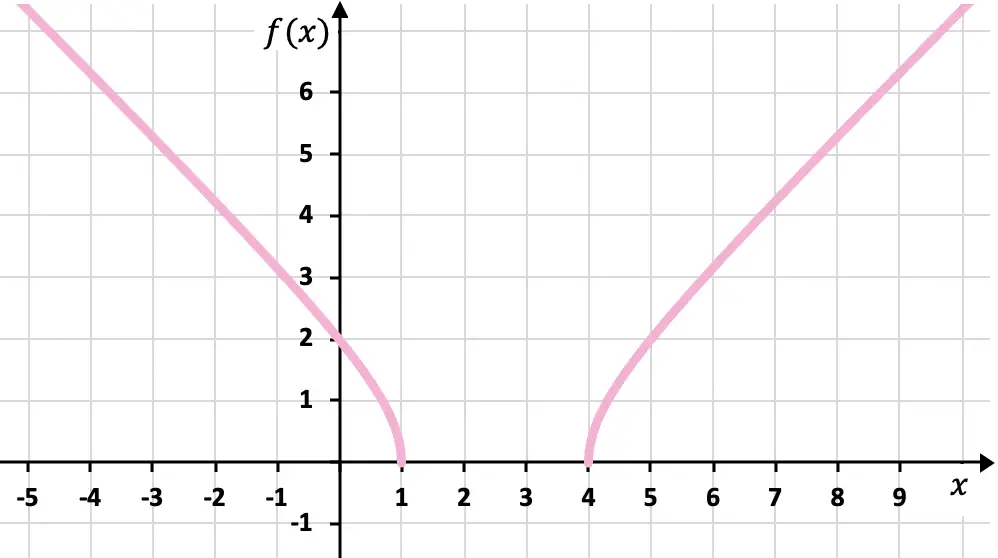
Zeichnen Sie die folgende irrationale oder radikale Funktion in ein Diagramm:

$f(x)= \sqrt{x^2-5x+4}$

Sehen Sie sich die Lösung an

Wir müssen zuerst den Definitionsbereich der Funktion berechnen:

$x^2-5x+4\ge 0$

In diesem Fall haben wir eine Ungleichung zweiten Grades erhalten, daher müssen wir die Formel für quadratische Gleichungen anwenden, um sie zu lösen:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

Wir teilen die Linie mit den erhaltenen Wurzeln in drei Teile:

Und wir ersetzen jeden Abschnitt der Ungleichung durch eine Zahl, um zu sehen, welche Abschnitte die Ungleichung erfüllen und daher zum Bereich gehören:

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=“Rendered by QuickLaTeX.com“> ❌ <p class=$ $x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$

$5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$

✅

Somit sind die Abschnitte, die die Ungleichung respektieren, die der Seiten:

Der Definitionsbereich der Funktion ist daher:

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

Nachdem wir den Definitionsbereich der Funktion berechnet haben, erstellen wir eine Wertetabelle, die die Werte der Funktion im Intervall des Definitionsbereichs angibt:

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

Abschließend stellen wir die erhaltenen Punkte im Diagramm dar und zeichnen die Funktion auf:

Graph einer irrationalen oder radikalen Funktion mit geradem Index

Übung 7

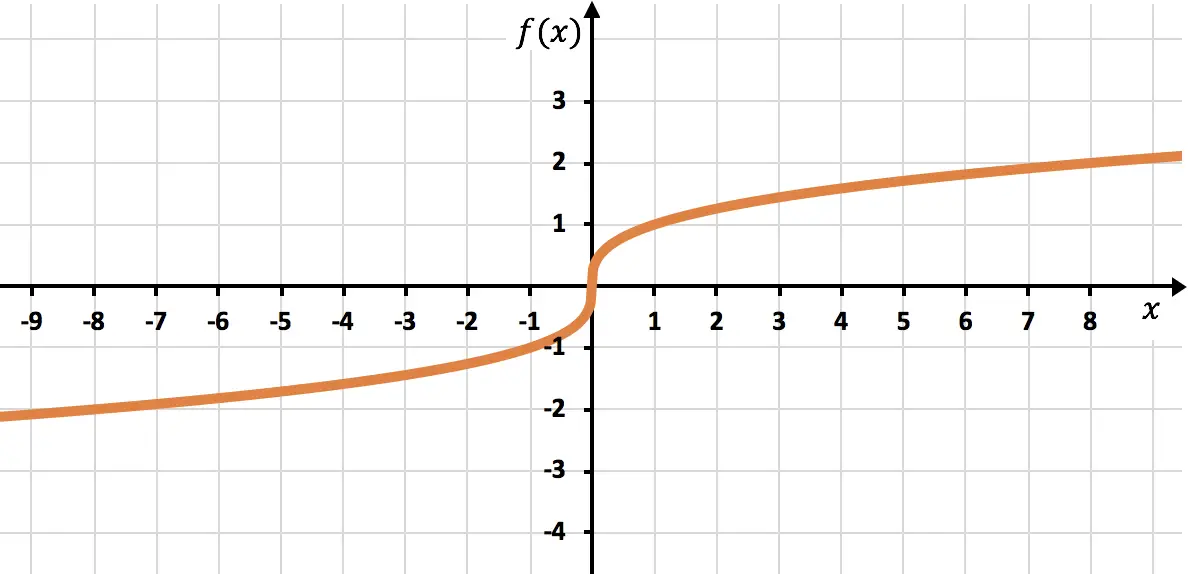
Stellen Sie im Diagramm die folgende durch eine Wurzel gebildete Funktion dar:

$f(x)= \sqrt[3]{x}$

Sehen Sie sich die Lösung an

Da es sich um eine irrationale Funktion handelt, deren Wurzel einen ungeraden Index hat, besteht der Definitionsbereich der Funktion aus reellen Zahlen:

$\text{Dom } f = \mathbb{R}$

Wir können daher jeden Punkt verwenden, um die Wertetabelle zu erstellen. In diesem Fall werden wir nach vielen Punkten suchen, da es sich um eine Kubikwurzel handelt:

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

Abschließend zeichnen wir die gefundenen Punkte ein und zeichnen die Funktion im Diagramm auf:

Zeichnen Sie eine irrationale oder radikale Funktion mit einem ungeraden Index

Übung 8

Lösen Sie das folgende Problem im Zusammenhang mit irrationalen (oder radikalen) Funktionen:

Der Verbrauch eines Handy-Akkus ergibt sich aus folgender Funktion:

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

Der Verbrauch wird in Milliampere (mA) ausgedrückt

$t$

ist die verstrichene Zeit in Minuten.

Bestimmen Sie den Wert der Konstante

$K$

so dass nach 4 Minuten der Verbrauch 35 mA beträgt.

Sehen Sie sich die Lösung an

Dass der Verbrauch nach 4 Minuten 35 mA beträgt, bedeutet, dass f(t) 35 ist, wenn t 4 ist. Also ist f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

Jetzt müssen wir die erhaltene Gleichung lösen. Wenn man genau hinschaut, handelt es sich um eine irrationale Gleichung, da sie eine Wurzel hat. Bei dieser Art von Gleichungen muss zunächst die Wurzel einer Seite isoliert werden, die in diesem Fall bereits isoliert ist. Nach der Isolierung müssen wir beide Seiten der Gleichung quadrieren:

$\left( \sqrt{4-K} \right)^2= 35^2$