雅可比和雅可比矩阵

在此页面上，您将通过示例了解什么是雅可比矩阵以及如何计算它。此外，您还有几个已解决的雅可比矩阵练习，以便您进行练习。您还将了解为什么雅可比矩阵的行列式雅可比如此重要。最后，我们解释该矩阵与其他操作之间的关系及其应用。

什么是雅可比矩阵？

雅可比矩阵的定义如下：

雅可比矩阵是由函数的一阶偏导数构成的矩阵。

因此雅可比矩阵的公式如下：

因此，雅可比矩阵的行数始终与标量函数的行数一样多

$(f_1,f_2,\ldots ,f_m)$

具有该功能，并且列数将对应于变量的数量

$(x_1, x_2, \ldots , x_n).$

另一方面，这个矩阵也称为雅可比微分图或雅可比线性图。事实上，有时也写成字母D而不是字母J：

$\displaystyle J_f = D_f$

出于好奇，雅可比矩阵以卡尔·古斯塔夫·雅可比 (Carl Gustav Jacobi) 的名字命名，卡尔·古斯塔夫·雅可比是一位 19 世纪重要的数学家和教授，为数学世界，特别是线性代数领域做出了重要贡献。

计算雅可比矩阵的示例

一旦我们了解了雅可比矩阵的概念，我们将通过示例逐步了解它是如何计算的：

确定以下函数在点 (1,2) 处的雅可比矩阵：

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

我们需要做的第一件事是计算函数的所有一阶偏导数：

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

现在我们应用雅可比矩阵公式。在这种情况下，该函数有两个变量和两个标量函数，因此雅可比矩阵将是维度为 2×2 的方阵：

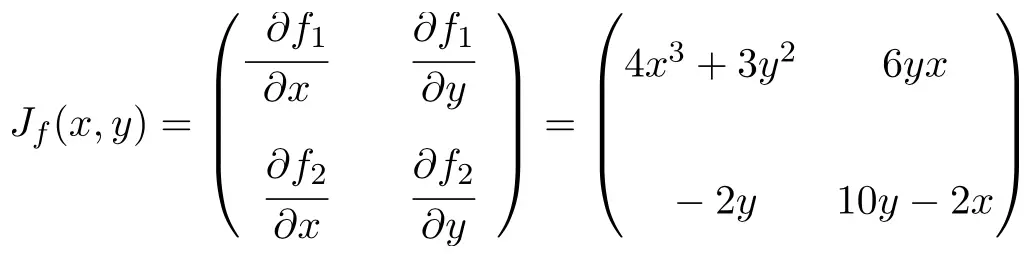
一旦我们有了雅可比矩阵的表达式，我们就在点 (1,2) 处计算它：

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

最后，我们进行运算，得到解：

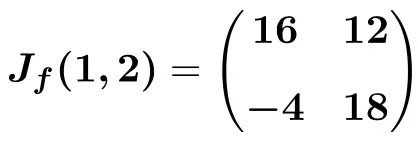
一旦您了解了如何求函数的雅可比矩阵，我们就会给您留下几个逐步解决的练习，以便您进行练习。

解决了雅可比矩阵的问题

练习1

求以下 2 个变量向量函数在点 (0,-2) 处的雅可比矩阵：

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

查看解决方案

该函数有两个变量和两个标量函数，因此雅可比矩阵将是大小为 2×2 的方阵：

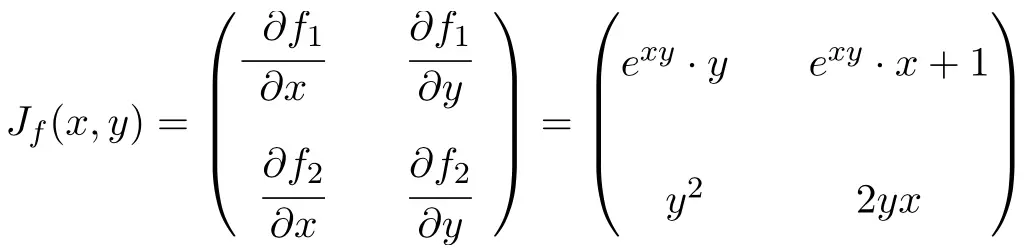
一旦我们计算了雅可比矩阵的表达式，我们就在点 (0,-2) 处对其求值：

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

最后，我们进行运算并得到结果：

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

练习2

计算以下具有 2 个变量的函数在点 (2,-1) 处的雅可比矩阵：

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

查看解决方案

在这种情况下，该函数有两个变量和两个标量函数，因此雅可比矩阵将是 2 阶方阵：

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

一旦找到雅可比矩阵的表达式，我们就在点 (2,-1) 处对其求值：

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

最后，我们进行运算并得到结果：

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

练习3

确定以下具有 3 个变量的函数在点 (2,-2,2) 处的雅可比矩阵：

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

查看解决方案

在这种情况下，该函数具有三个变量和两个标量函数，因此雅可比矩阵将是一个维度为 2×3 的矩形矩阵：

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

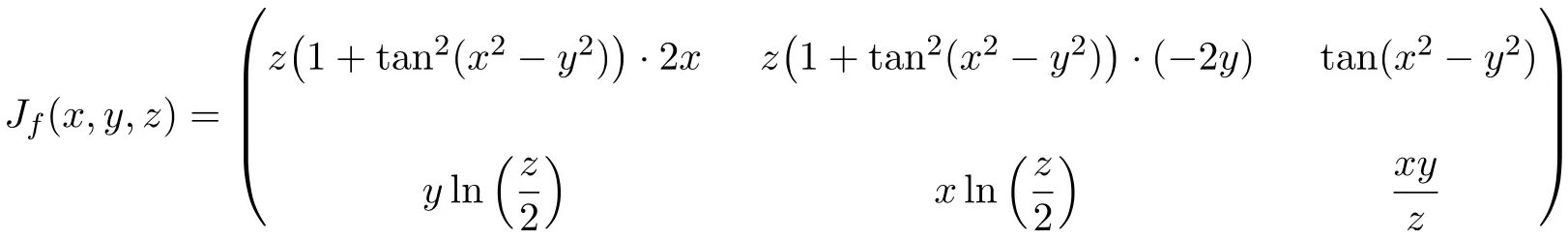
一旦我们有了雅可比矩阵的表达式，我们就在点 (2,-2,2) 处对其求值：

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

我们进行计算：

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

而我们继续运算，直到不能再简化为止：

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

练习4

确定该点的雅可比矩阵

$(\pi, \pi)$

以下多变量函数的：

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

查看解决方案

在这种情况下，该函数有两个变量和三个标量函数，因此雅可比矩阵将是一个维度为 3×2 的矩形矩阵：

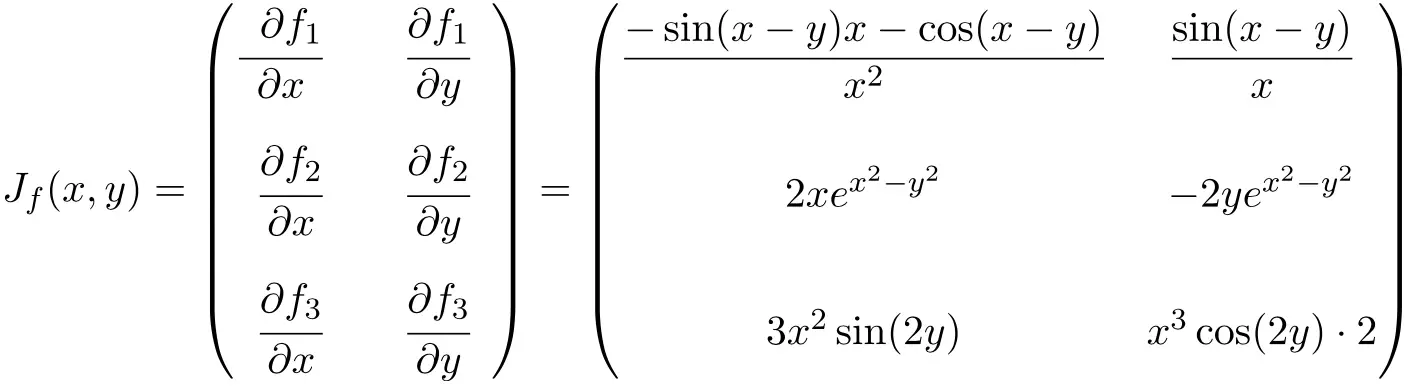
一旦我们有了雅可比矩阵的表达式，我们就可以将其计算为点

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

我们进行以下操作：

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

因此，在所考虑的点处，向量函数的雅可比矩阵的值为：

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

练习5

计算该点的雅可比矩阵

$(3,0,\pi)$

以下具有 3 个变量的函数：

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

查看解决方案

在这种情况下，函数由三个变量和三个标量函数组成，因此，雅可比矩阵将是维度为 3×3 的方阵：

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

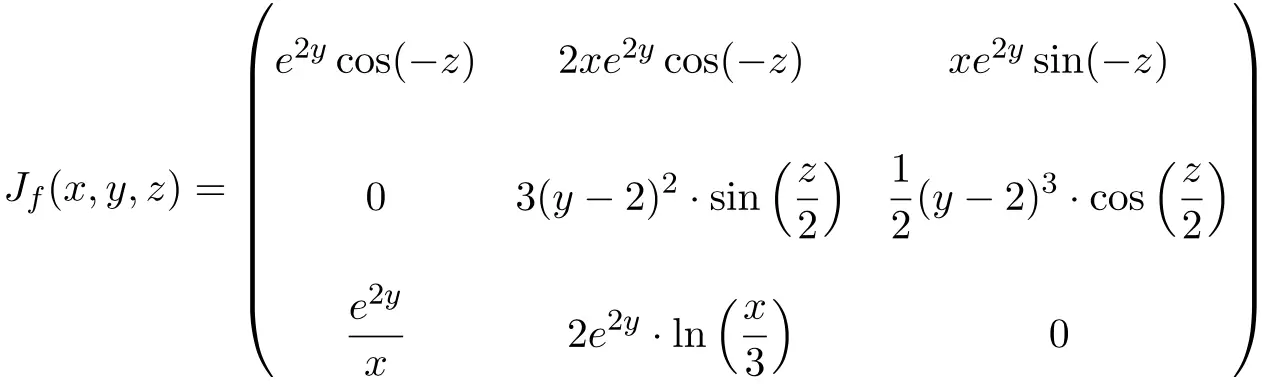
一旦我们找到了雅可比矩阵，我们就在该点对其进行评估

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

我们计算操作：

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

且该点的雅可比矩阵结果为：

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

雅可比矩阵的行列式：雅可比

雅可比矩阵的行列式称为雅可比行列式或雅可比行列式。必须考虑到，只有当函数与标量函数具有相同数量的变量时，才能计算雅可比矩阵，因为这样雅可比矩阵将具有与列数相同的行数，因此它将是一个方阵矩阵。。

雅可比行列式的例子

让我们看一个计算具有两个变量的函数的雅可比行列式的示例：

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

我们首先计算函数的雅可比矩阵：

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

现在我们求解 2×2 矩阵的行列式：

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

雅可比行列式和函数的可逆性

现在您已经了解了雅可比行列式的概念，您可能会想……这有什么意义呢？

那么，雅可比行列式的主要用途是确定函数是否可以反转。反函数定理指出，如果雅可比矩阵（雅可比行列式）的行列式不为 0，则意味着该函数是可逆的。

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

需要注意的是，这个条件是必要的，但不是充分的，也就是说，如果行列式非零，我们可以断言矩阵可以求逆，但是，如果行列式为0，我们无法知道是否函数有一个反函数或No。

例如，在前面看到的如何查找函数的雅可比行列式的示例中，行列式给出

$4x^2+4y^2$

。在这种情况下，我们可以断言除了点 (0,0) 之外，该函数总是可以反转，因为该点是唯一雅可比行列式等于 0 的点，因此，我们不知道反函数是否存在于这一点。

雅可比矩阵与其他运算的关系

雅可比矩阵与函数的梯度和Hessian矩阵有关：

坡

如果函数是标量函数，雅可比矩阵将是行矩阵，相当于梯度：

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$