逆波兰表示法(RPN)是程序员可能遇到的最常见的操作之一。该表示法由数学家Jan Łukasiewicz于 1920 年引入,专门用于简化极大的数学表达式。此外,这种类型的表示法目前在科学计算器领域广泛使用,因此我们建议您跟随我们学习如何正确使用它。
在什么地方或什么类型的数学运算中您会遇到逆波兰表示法?
这种数学语言常见于算术、代数中,是每个系统工程师都应该非常熟悉的一种操作语言。随着时间的推移,这种类型的数值运算或表达式已被认为是显着减少计算机内存使用的绝佳替代方案。自从发现这一点以来,它的使用已经扩展到世界上的每个操作系统。因此,它可以快速编程,从而节省大量时间。
在大多数情况下,程序员花费比预期更多的时间来开发应用程序和操作系统、网页等的操作。要在编程中应用逆波兰表示法,您需要使用数学运算的 LIFO(后进先出)结构。这种类型的过程基于这样一个事实:不必将整个操作按顺序放置即可找到我们期望的结果。最好用一个例子来解释它:
假设我们需要编写一个自动国际货币兑换页面,首先我们需要放置所有参数,在这种情况下我们将使用美元和欧元。基本上,运算可以是A x B = C假设 A 是美元,B 是欧元的美元价值。
在执行该操作时,我们显然会得到需要购买估计数量的欧元的美元,但是在对页面进行编程时,该操作必须是自动的。这就是应用逆波兰表示法的原因,在这种情况下,它将表示为:AB x,因此结果为 C,将自动应用在页面上。
如何正确构造逆波兰表示法?
顾名思义,逆波兰表达式本质上是将操作数放在第一位(这将是我们需要除法、乘法等的数字),然后是运算符。在这种情况下,运算符将是乘法、除法、加法以及其他过程,当然,一个简单的示例可以让您了解上下文,不会有什么坏处,所以我们将在下面表示它。
AB+
假设A是15,B是45,以这种方式编程系统将立即识别出我们正在指的是数学运算,因此我们将立即找到c。在本例中为 65。
如果您学习编程,您会更快地理解我们下面介绍的代码。
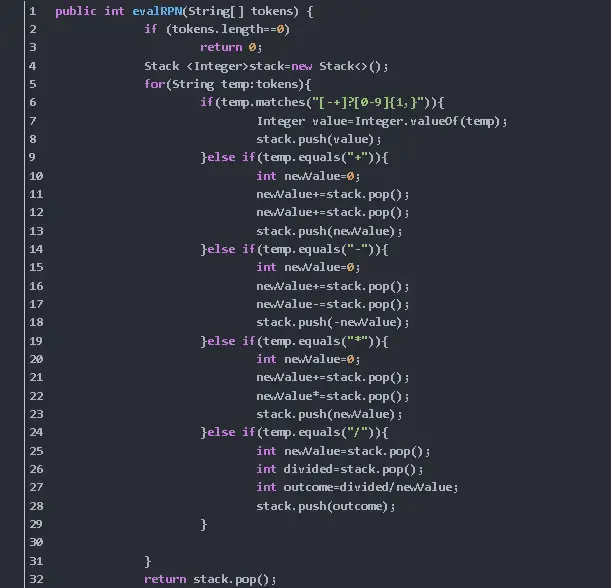
它提供了一个简单的操作,无需编程,用逆波兰表示法表示如下。
1) [“2”, “1”, “+”, “3”, “*”] -> ((2 + 1) * 3) -> 9
2) [“4”, “13”, “5”, “/”, “+”] -> (4 + (13 / 5)) -> 6
运行分析:
必须考虑到此操作必须是堆栈,并且具有特殊的除法和减法倾向。首先,我们需要摆脱分割,提取第一个括号内的所有数据。一旦计算出来,这个新值就被放入堆栈中,当然整个过程会给出数字6,考虑到每个操作都是相互独立的,我们以数字2为例。
反转波兰表示法可以给您带来什么好处?
- 您想要表达的任何类型的数学运算的计算都将按顺序进行,因此我们在创建任何类型的复杂运算时会出现更少的错误。
- 它不需要使用括号或任何类型的代数规则,因为我们正在添加信息,所以任何操作都是分步计算的。
- 对于编程或任何类型工程的学生来说,理解正在完成的操作变得更加容易。
- 在没有深入的算术知识的情况下将任何类型的数学运算直接复制到计算器上可能会导致错误,这就是应用 NPI 更实用的原因。
- 您不应使用= 符号来查找您期望的结果。
最推荐使用哪些计算器来应用 NPI(逆波兰表示法)?
计算器对于任何学生来说都是最好的工具,但在大多数情况下,它们仅被设计用于解决简单的运算,并且它们的配置方式与通常编写的方式相同。因此,如果您正在寻找一款可以处理逆波兰表示法的计算器,您将需要一个更简单的计算器,最受程序员欢迎的是HP 50G 。
虽然还有其他计算器可以在线表达这些类型的操作(许多HP 计算器可能是一个不错的选择),但当然,拥有一个专门的计算器可以加快编程过程。
我们可以强调其优点:
- 特别适用于复杂方程的内置库。
- 超过 300 个带有科学常数的自动公式,适用于任何类型的逆波兰表示法运算。
- 有了它,您可以比预期更快地开发应用程序。
- 它也符合常见科学计算器的标准,因此逆波兰表示法可能是它的强项,但它也适用于其他类型的运算。
逆波兰表示法极大地改变了编程系统,毫无疑问,建议应用它来获得准确的结果,而不会出现常见的计算错误。您还在等什么来获得您的呢?最后,我们建议您查看我们关于数学表示法的文章,因为它可以很好地补充本文中学到的有关逆波兰表示法(RPN)的信息。