计算最小公倍数 (lcm)

两个或多个数字的最小公倍数 (LCM)是这些数字共有的最小（非零）倍数。它是最大公约数的逆运算，尽管它是使用类似的方法计算的。如果您想学习如何计算 LCM，我们建议您继续阅读，因为在本文中我们将解释查找一组数字的最小公倍数的所有过程（从最简单到最复杂）。

液晶显示计算器

在我们开始讨论如何获得 lcm 之前，我们想让您知道，在此页面上我们有一个最小公倍数计算器。有了它，你将能够计算出所有你想要的数字的lcm，这样你就可以比较你的练习结果，看看你是否正确地解决了它们。

要使用不太常见的倍数计算器，请输入用逗号分隔的整数：

计算lcm

如何计算最小公倍数？

要找到两个或多个数字的最小公倍数，您需要遵循我们将在下面解释的三种方法之一。接下来，当我们详细介绍您可以选择的每个程序时，我们也会告诉您它们的优点和缺点。这样您就知道在每种情况下应该选择哪一个，从而轻松快速地解决有问题的 LCM。

方法一：多重列表

第一种方法是创建要在 LCM 中计算的数字的倍数列表。然后你需要找到所有列表中重复的最小值，这样你就得到了最小的公倍数。然后我们将通过一个例子来了解它：lcm (5, 6)。

方法二：阶乘分解

其次，我们可以选择对数字进行因式分解。更具体地说，这种方法将使计算大数的 pcm变得更容易。由于在执行大数的 lcm 时遵循方法 1 可能会很慢且乏味，仅仅是因为我们必须编写很长的倍数列表。第二个过程一开始理解起来可能有点复杂，但是当您了解其机制时，它与前一个过程相比有很多优点。也就是说，让我们看看要遵循的程序：

• 阶乘分解：第一步是将 LCM 中包含的所有数字分解为质因数。如果您不知道如何分解数字的阶乘，我们建议您输入最后一个链接，在那里您将找到有关如何快速有效地简化数字的一流解释。
• 创建一个数学表达式：当我们将所有数字都表示为质因数时，我们将选择求最大指数的常见数字和非常见数字。然后你把它们写成一个单一的数学表达式，最后你解决必要的乘法和/或幂。这样你就已经得到了 lcm 的数值。

方法三：数学公式

获得最小公倍数的最后一种方法是使用 GCD 和以下数学公式：

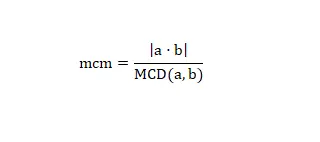
使用这个公式我们可以计算任何数字的lcm。让我们看一个真实的例子，如果我们要计算 lcm (2.6)，我们只需要求解 (2 x 6) / 2 = 6 运算。我们已经解决了计算，你可以看到这是一个简单的方法如果您有 GCD 或者可以轻松计算它，那么速度会很快。

快速计算lcm的技巧

当你掌握了我们刚才讲解的三种方法后，我们建议你阅读一下我们现在要讲的最小公倍数的性质。由于有了它们，您将能够识别一些可以非常快速地计算 LCM 的特定情况，而无需使用已经解释过的策略。

• 第一个数能被第二个数整除：如果我们想计算a除b时a和b的最小公倍数，那么这两个数的ppcm将是最大的（在本例中为b）。例如，如果要计算 2 和 8 的 lcm，则结果将是最大的，因此为 8。
• 两个素数：在求两个素数的情况下，最快的方法是将它们相乘，结果就是 ppm。这是合乎逻辑的，因为它的最大公约数是 1，这意味着我们无法将数字分解为比数字本身更简单的因子，因此我们只能将它们相乘。例如，3 和 5 的最小公倍数将是它们乘积的结果：3 x 5 = 15。

如何求分数中的最小公倍数？

当我们想要求解分数的加法或减法时，我们需要计算最小公分母，它与 lcm 相同，但适用于分数。基本上，我们正在寻找两个分母的 lcm，以便我们可以将总和表示为一个分数。如果您想了解最小公分母如何应用于实分数计算，可以输入此链接。

科学计算器上的 Lcm

任何科学计算器上都有 LCM 键，可让您计算两个整数的最小公倍数。对于卡西欧计算器，您需要遵循的语法或过程如下。首先，按APHA + MCM （最后一个键将标记为棕色）。完成此操作后，您可以输入两个数字，但请记住必须用逗号（ SHIFT + , ）分隔它们。最后，单击等于按钮即可获得最小公倍数。

LCM练习一步一步解决

接下来，我们将向您展示三个逐步求解最小公倍数的示例。通过这种方式，您可以尝试解决这些问题并练习一些我们在本文中解释的内容。如果你想内化概念，尝试解决练习很重要，因为有必要将理论应用到现实中。也就是说，我们让您练习以下练习：

计算 4 和 6 的 lcm

计算 6 和 9 的 lcm

计算30和40的lcm