您肯定听说过虚数集或虚数单位。它是一个数学概念,源于表达不属于实数的数字的数学需要。
什么是虚数?
虚数是那些平方后得到负数的数。因此,这些是相当于负数的平方根的值。例如,虚数单位(数字 i)等于 -1 的平方根。
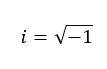
这些数不属于实数,因为在实数集中负根无法解。这就是想象场景的重要性所在。发明这个集合是为了能够处理负根,并能够解决所有“无解”的方程和二次问题,因为它们给我们一个负根。
为了避免混淆,区分虚数和复数很重要。复数是由一个实数和一个虚数组成的数。因此,虚数是复合体的一个子类别,它没有实部。在下表中,您将能够更好地理解这些差异。
| 复数 | 皇家派对 | 想象部分 | 描述 |
| 4+7i | 4 | 7i | 复杂的 |
| 3 | 3 | 0 | 纯粹的皇家 |
| 2i | 0 | 2i | 纯粹的想象 |
为了完成这个数字集的定位,我们可以在下图中可视化所有集的结构。正如我们所看到的,复数涵盖了所有类型的数字,这些数字又可以分为实数和纯虚数(这是我们在本文中讨论的)。

虚数的例子
从虚数单位(i),我们可以推导出其他虚数。您只需应用以下公式:
m = ri
其中m是虚数,r是实数,i是虚数单位。在下图中,您可以看到我们如何从负根得到不同的虚数。
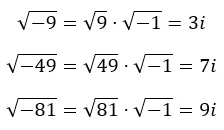
事实上,我们可以将其推断为以下表达式:
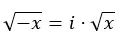
虚数的性质
虚数有许多非常有趣的性质。有些我们已经在本文开头讨论过,有些则没有:
- 想象不属于现实的集合,因为它们是物理上不存在的数字,无法在我们的现实中表示。
- 这些是相当于负根的值。
- 它们可以在假想线上以图形方式表示。
- 虚数幂(这是我们将在下一节中解释的概念)对于简化涉及虚数的数值计算有很大帮助。
- 欧拉公式是一个可以将虚数与实数联系起来的表达式。
虚数运算
现在您已经了解了虚数的所有重要特征,是时候学习如何用它们来解决运算了。要使用虚数进行操作,您必须遵循与实数进行操作相同的步骤,不同之处在于您必须考虑一个概念:虚数幂。
想象力
虚数有一个非常有趣的性质,当你将虚数单位乘以它本身时就会出现这种性质。也就是说,当你产生虚统一的力量时,就会发生这种情况。如果我们写下权力,如下表所示,可以发现一种模式:
我0 = 1
我1 =我
i 2 = i · i = ( √ -1) · ( √ -1) = -1
i 3 = i 2 i = (-1) i = -i
i 4 = i 2 i 2 = (-1) (-1) = 1
了解这个概念将使我们更容易解决虚数运算,因为我们将能够简化困难的运算并使它们变得更容易一些。此外,这些能力的好处是它们可以无限期地重复。如果我们再添加一些权力,我们可以看到这一点:
我5 = 我
我6 = -1
我7 = -i
我8 = 1
ETC。
对于负能量,这种情况也会发生。
虚数的算术运算
接下来,我们将为您提供每个基本算术运算的示例,以便您可以看到已解决的虚数计算。
- 虚数相加:与实数相加完全相同,只是别忘了加上 i。
4i + 3i = 7i
- 虚数减法:减法的解法也与实数集相同。
4i – 3i = 我
- 虚数的乘法:在这种情况下,我们必须记住我们之前提到的虚数幂。
3i 4i = 12 i 2 = 12 (-1) = -12
- 虚数除法:在这种除法中我们也必须保持警惕,以防遇到虚数幂,它可以让我们简化运算。
12i ÷ 4i = 3
虚数方程
正如我们之前所说,当我们求解实数集中的方程时,有时我们会得到负根,因此方程“无解” 。但是,既然我们知道了虚数,我们就可以解这些方程了。让我们看一个例子:
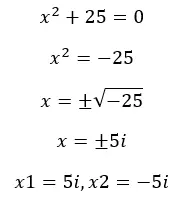
虚数有什么用?
虚数的产生是因为需要能够表达实数集之外的值。这就是为什么乍一看它们似乎没有很多有用的应用程序。但事实却恰恰相反。因为当我们将它们与实数结合起来时,我们得到了复数。
这些有很多应用。它们用于研究交流电(因为它具有负值),其用途在波领域也非常广泛(在物理学、电信电子学和量子力学中都有应用)。除许多其他用途外。
另外,经常会发生这样的情况:当你解二次方程时,该值给你一个负根,你无法运算……用虚数你可以解它们。因此,作为结论,我们可以说它是一个允许我们扩展更抽象知识的集合。