线段中间的公式

16 9 月, 2023

本页解释线段中点的含义。此外，您还将了解如何使用公式找到线段的中间位置。您甚至会看到示例、练习和已解决的线段中点问题。

线段的中点是什么？

在数学中，线段的中点是与线段端点距离相同的点。因此，中间将段分为两个相等的部分。

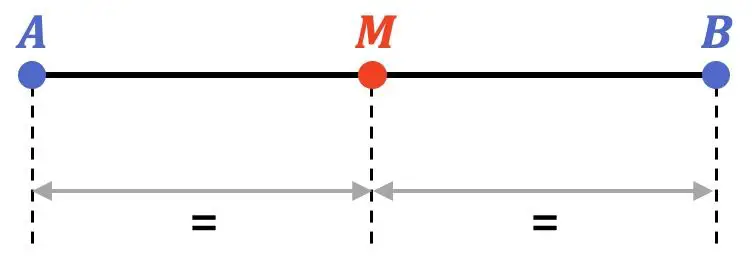
线段中间的定义

此外，中点位于线段的中心，因此属于线段的平分线。

另一方面，线段的中点也是与两个几何元素（线段的两端）等距的点。

如何计算线段的中点？

给定线段极值点的笛卡尔坐标：

$A(x_1,y_1) \qquad B(x_2,y_2)$

所述线段的中间坐标对应于极值点坐标的一半和：

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

这是笛卡尔平面（R2 中）中线段中间的公式。但显然该公式也适用于笛卡尔空间（在R3中），只需添加Z坐标的半和即可：

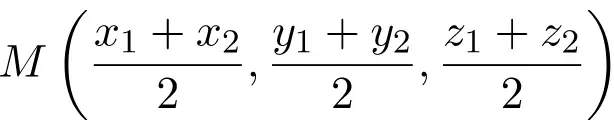
让我们看一个如何计算线段中点坐标的示例：

确定由以下点形成的线段的中点：

$A(2,5) \qquad B(4,-1)$

要找到线段的中间，只需应用其公式：

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

在片段中间解决的练习

练习1

端点为以下两点的线段的中点是多少？

$A(3,-2) \qquad B(5,8)$

查看解决方案

要找到线段的中间，您必须直接应用以下公式：

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

练习2

求从 A 点开始、中点为 M 的线段的端点坐标。

$A(4,-1) \qquad M(-2,1)$

查看解决方案

在这种情况下，我们知道起始点和线段中间的坐标。因此，我们将已知的坐标代入线段中点的公式中：

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

现在我们从前面的方程中解出线段终点的坐标：

X坐标

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

Y坐标

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

因此，线段最终末端的坐标为：

$\bm{B(-8,3)}$

练习3

给定以下平行四边形：

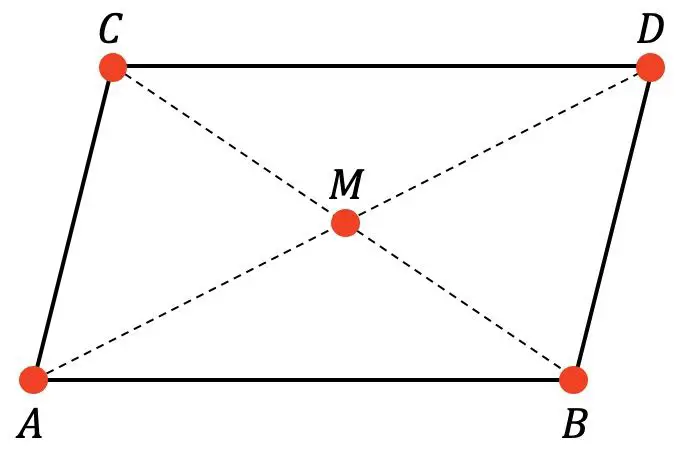
段 4 的中间

我们知道M是平行四边形的中心，A、B、C点的坐标为：

$A(1,1) \quad B(5,1) \quad C(7,3)$

根据此信息并使用中点公式计算 D 点的坐标。

查看解决方案

要使用线段中点公式求出 D 点的坐标，必须先计算 M 点的坐标，然后计算 D 点的坐标。

M点是线段BC的中点，因此它的坐标为：

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

一旦我们知道了M点，我们就可以找到D点。M点也是线段AD的中间，所以：

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

D点X坐标

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

D点Y坐标

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

因此 D 点的坐标为：

$\bm{D(11,3}$

练习4

计算垂直于线段 PQ 中点的直线的连续方程。成为要点

$P(1,4)$

和

$Q(5,-2).$

查看解决方案

为了确定直线的方程，我们需要它的方向向量和直线一部分的点。

在这种情况下，线的方向向量将垂直于向量

$\vv{PQ}.$

因此我们计算向量

$\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

我们可以通过改变向量之间的向量分量，然后改变分量的符号来找到垂直于另一个向量的向量，因此：

$\vv{PQ}_\perp =(6,4)$

现在我们有了直线的方向向量，因此我们只需要一个属于直线的点。在本例中，指令告诉我们直线穿过线段的中点，因此我们使用以下公式计算中点：

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

最后，我们根据计算出的点和向量构造直线的连续方程：

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

发表评论取消回复