Hessian 矩阵（或 Hesse）-

本页无疑是现有的 Hessian 矩阵最完整的解释。这里解释了Hessian矩阵的概念，如何用例子计算它，甚至还有几个已解决的练习可供练习。此外，您将能够了解如何计算多变量函数的最大值和最小值，以及它是凹函数还是凸函数。最后，您还将找到 Hessian 矩阵实用程序和应用程序。

什么是 Hessian 矩阵？

Hessian（或Hessian）矩阵的定义如下：

Hessian 矩阵是由 n 个变量的函数的偏二阶导数组成的维度为 n × n 的方阵。

这个矩阵也被称为Hessian，甚至在一些数学书籍中它被命名为Discriminant。但最常见的称呼方式是 Hessian 矩阵。

因此Hessian矩阵的公式如下：

因此，Hessian 矩阵始终是方阵，其维度等于函数中变量的数量。例如，如果函数有 3 个变量，则 Hessian 矩阵的维度为 3×3。

此外，施瓦茨定理（或克莱罗定理）指出，微分的顺序并不重要，即首先对变量进行部分推导

$x_1$

那么关于变量

$x_2$

相当于部分微分

$x_2$

然后尊重

$x_1$

。

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

因此，Hessian矩阵是一个对称矩阵，或者换句话说，它具有以其主对角线为轴的对称性。

出于好奇，Hessian 矩阵是以 19 世纪德国数学家 Ludwig Otto Hesse 的名字命名的，他对线性代数领域做出了非常重要的贡献。

计算Hessian矩阵的示例

让我们看一个如何查找 2 × 2 维 Hessian 矩阵的示例：

计算以下函数的 (1,0) 点处的 Hessian 矩阵：

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

首先，我们需要计算一阶偏导数：

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

一旦我们知道一阶导数，我们就可以计算所有二阶偏导数：

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

因此，我们现在可以从 2 × 2 矩阵的公式中找到 Hessian 矩阵：

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

因此，在 (1,0) 点计算的 Hessian 矩阵将是：

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

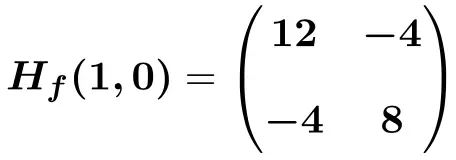
解决了 Hessian 矩阵的问题

练习1

计算以下函数在点 (1,1) 处具有 2 个变量的 Hessian 矩阵：

$\displaystyle f(x,y)=x^2y+y^2x$

查看解决方案

首先，我们需要求函数的一阶偏导数：

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

一旦我们计算了一阶导数，我们就继续求解所有二阶偏导数：

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

因此Hessian矩阵定义如下：

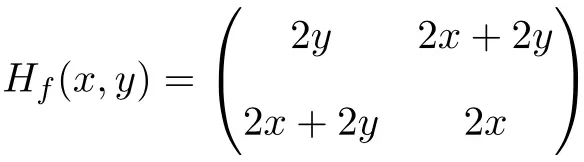
最后，剩下的就是计算点 (1,1) 处的 Hessian 矩阵：

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

练习2

计算以下函数在两个变量中的点 (1,1) 处的 Hessian：

$\displaystyle f(x,y)= e^{y\ln x}$

查看解决方案

首先，我们需要计算函数的一阶偏导数：

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

一旦我们有了一阶导数，我们就可以计算函数的二阶偏导数：

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

因此函数的 Hessian 矩阵是维度为 2×2 的方阵：

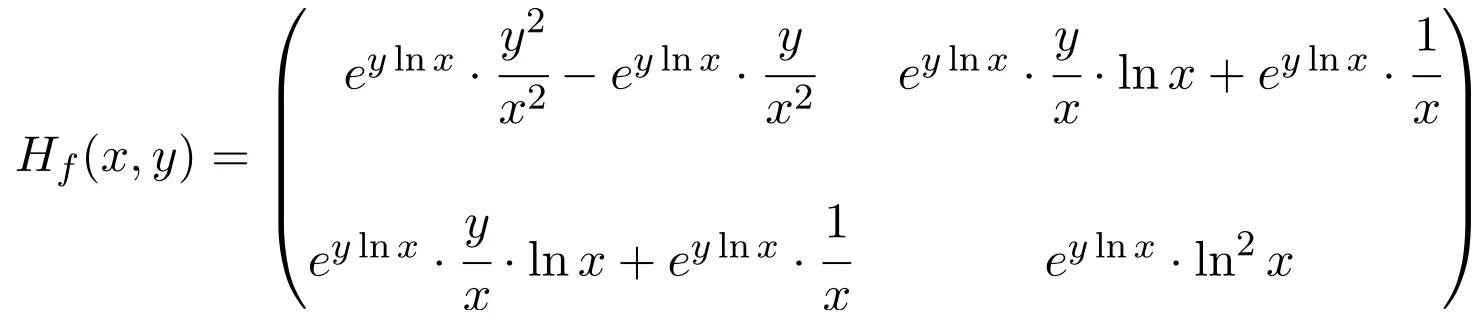
最后，剩下的就是计算点 (1,1) 处的 Hessian 矩阵：

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

练习3

求该点的 Hessian 矩阵

$(0,1,\pi)$

以下具有 3 个变量的函数：

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

查看解决方案

首先，我们计算函数的一阶偏导数：

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

一旦我们有了一阶导数，我们就可以计算函数的二阶偏导数：

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

则函数的 Hessian 矩阵是维度为 3×3 的方阵：

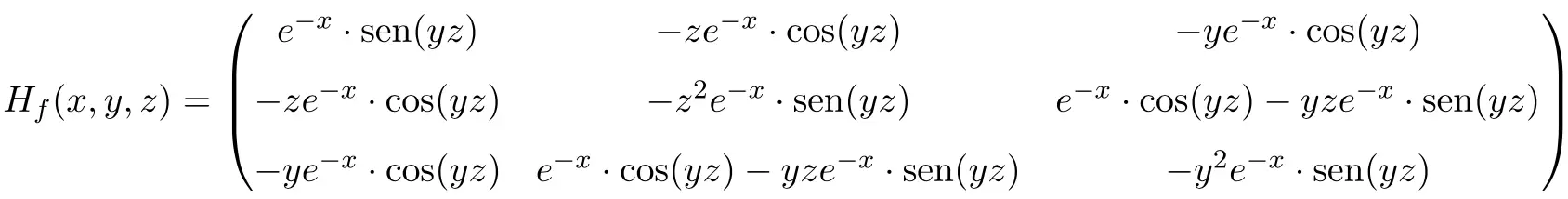
最后，我们将变量替换为它们在该点各自的值

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

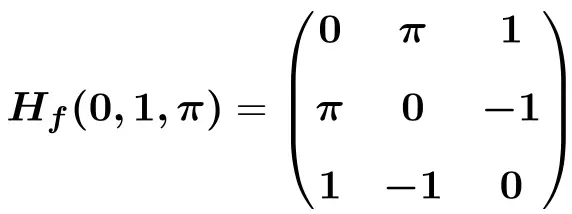
练习4

确定以下具有 4 个变量的函数在点 (2,-1,1,-1) 处的 Hessian 矩阵：

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

查看解决方案

第一步是求函数的一阶偏导数：

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

现在我们求解函数的二阶偏导数：

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

因此求解所有偏导数得到的4×4 Hessian矩阵的表达式为：

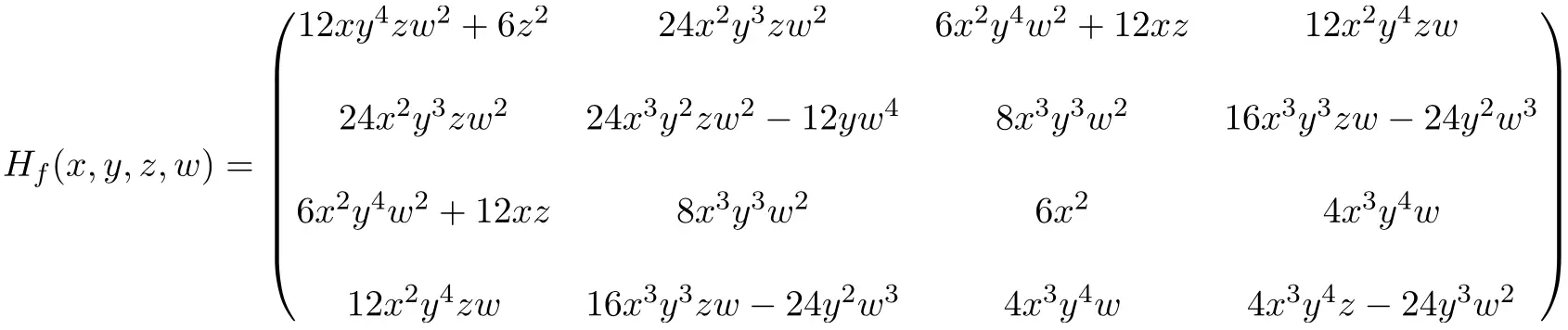
最后，我们将未知数替换为它们各自的点值（2，-1，1，-1）并进行计算：

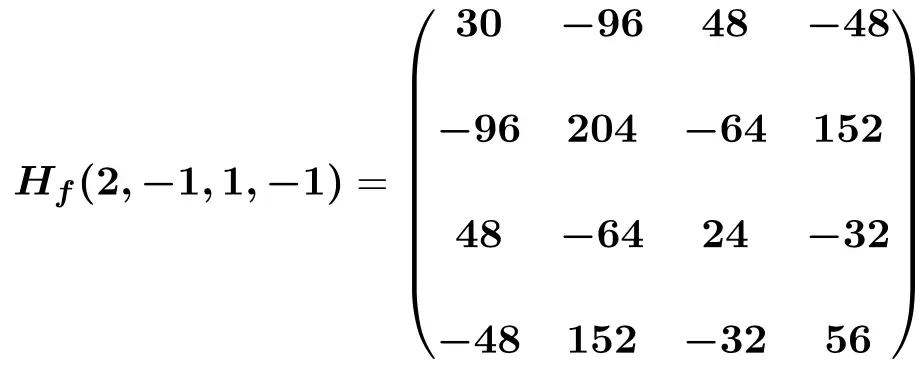
如何知道Hessian矩阵何时为正、负或不定？

正如我们稍后将看到的，知道 Hessian 矩阵是正半定、正定、负半定、负定还是不定矩阵是非常有用的。那么让我们看看如何找出答案：

特征值（或特征值）的准则

知道它是什么类型的矩阵的一种方法是通过Hessian矩阵的特征值（或特征值）：

如果 Hessian 矩阵的特征值（或多个特征值）等于且大于零，则该矩阵是正半定的。也就是说，它具有正特征值且至少有一个等于0：

$\lambda \geq 0$

如果 Hessian 矩阵的所有特征值（或多个特征值）都完全大于 0（正），则 Hessian 矩阵是正定的：

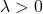$\lambda > 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <ul> <li>如果 Hessian 矩阵的特征值（或多个特征值）等于且小于零，则该<span style=$ 矩阵是负半定的。也就是说，它具有负特征值且至少有一个等于0：

$\lambda \leq 0$

如果 Hessian 矩阵的所有特征值（或多个特征值）都小于 0（负），则 Hessian 矩阵是负定的：

$\lambda < 0$

当Hessian矩阵有正负特征值（或特征值）时，它是未定义的：

$\lambda > 0 \qquad \lambda <0$

西尔维斯特准则

知道Hessian矩阵是什么类型的另一种方法是使用西尔维斯特准则，尽管这个定理只能让我们知道它是正定、负定还是不定。但有时它的使用速度会更快，因为计算通常更容易。

因此，西尔维斯特准则如下：

如果Hessian矩阵的所有主次数都大于0，则它是正定矩阵。

如果 Hessian 矩阵的主次数为偶数且大于 0，且奇数数小于 0，则为负定矩阵。

如果Hessian矩阵的所有主次数都不为0并且前两个条件都不满足，则它是不定矩阵。

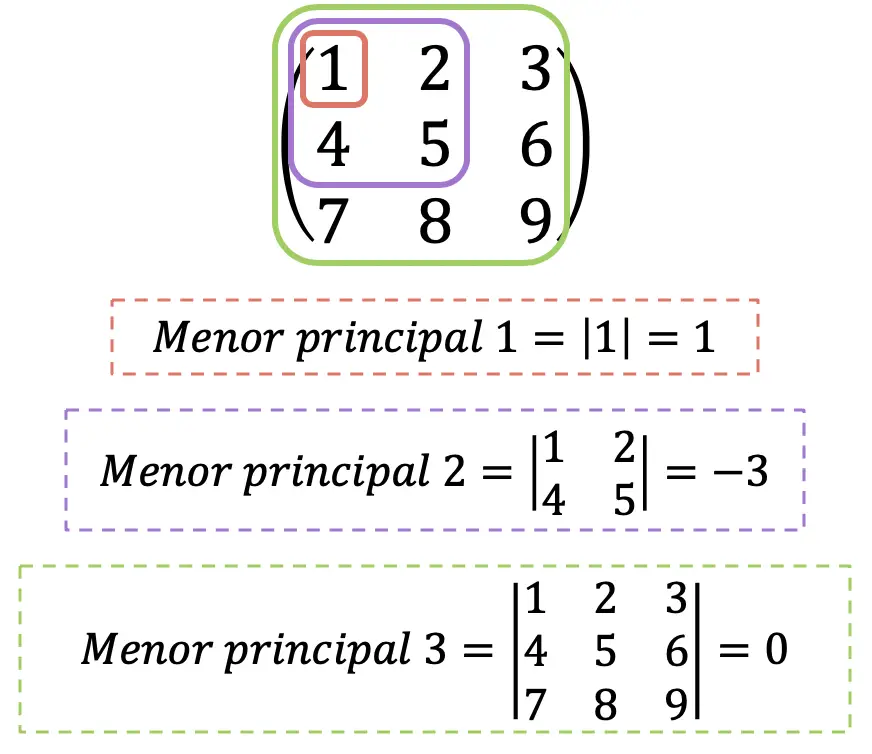
显然，Hessian矩阵的最大主次数总是与其行列式一致。仅供参考，Hessian 矩阵的行列式也称为“Hessian”，尽管为了避免混淆我们在这里不会这样做。

如何使用 Hessian 矩阵计算函数的最大值或最小值

一旦您知道如何计算 Hessian 矩阵，您可能想知道：这个矩阵有什么用？

嗯，Hessian 矩阵的应用之一就是求具有多个变量的函数的最大值或最小值。以下是如何计算最大值和最小值的分步说明：

首先，计算多变量函数的临界点。为此，我们计算函数的梯度或雅可比矩阵，将其设置为 0 并求解方程。
计算Hessian矩阵。
将步骤1中找到的临界点代入Hessian矩阵中。因此，我们将获得与临界点具有该函数一样多的 Hessian 矩阵。
我们看看每个 Hessian 矩阵是什么类型的矩阵。也就是说，我们看看它是否是正定、负定、不定等。
- 如果Hessian矩阵是正定的，那么临界点就是函数的相对最小值。
- 如果Hessian矩阵是负定的，那么临界点就是函数的一个相对最大值。
- 如果Hessian矩阵未定义，则临界点是鞍点。

计算多变量函数的最大值和最小值的示例

为了了解这是如何完成的，下面是使用 Hessian 矩阵计算和分类函数的相对极值的示例：

求以下多变量函数的所有相对极值：

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

我们需要做的第一件事是计算函数的雅可比矩阵，在本例中它将与梯度一致，因为它是一个标量函数：

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

现在我们必须确定临界点，为此，我们将获得的方程等于 0，并求解方程组：

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

所以我们找到的临界点是(0,-2)。

一旦找到函数的临界点，我们就必须计算Hessian矩阵：

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

并且，显然，在临界点评估的 Hessian 矩阵是相同的：

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

为了了解它是什么类型的矩阵，我们将使用西尔维斯特准则。因此，我们求解矩阵的主要次要项：

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

主次数 1（奇数）为正，主次数 2（偶数）为负，因此根据西尔维斯特准则，它是一个不定矩阵。因此，临界点 (0,-2) 是鞍点。

使用 Hessian 矩阵确定函数的凹性或凸性

Hessian矩阵的另一个用途是知道一个函数是凹函数还是凸函数。这可以根据以下定理来确定：

是

$A \subseteq \mathbb{R}^n$

一个开集和

$f \colon A \to \mathbb{R}$

二阶导数连续的函数，其凹凸由 Hessian 矩阵定义：

功能
$f$

整体呈凸形

$A$

当且仅当其 Hessian 矩阵在集合的每个点都是半正定的。
功能
$f$

整个过程都是严格凸的

$A$

当且仅当其 Hessian 矩阵在集合的每个点都是正定的。

✓因此，如果

$f$

是雅可比矩阵也消失的点处的凸函数，该点是局部最小值。

功能
$f$

整体呈凹形

$A$

当且仅当其 Hessian 矩阵在集合的每个点都是负半定的。
功能
$f$

整体是严格凹的

$A$

当且仅当其 Hessian 矩阵在集合的每个点都是负定的。

✓因此，如果

$f$

是雅可比矩阵也消失的点处的凹函数，该点是局部最大值。

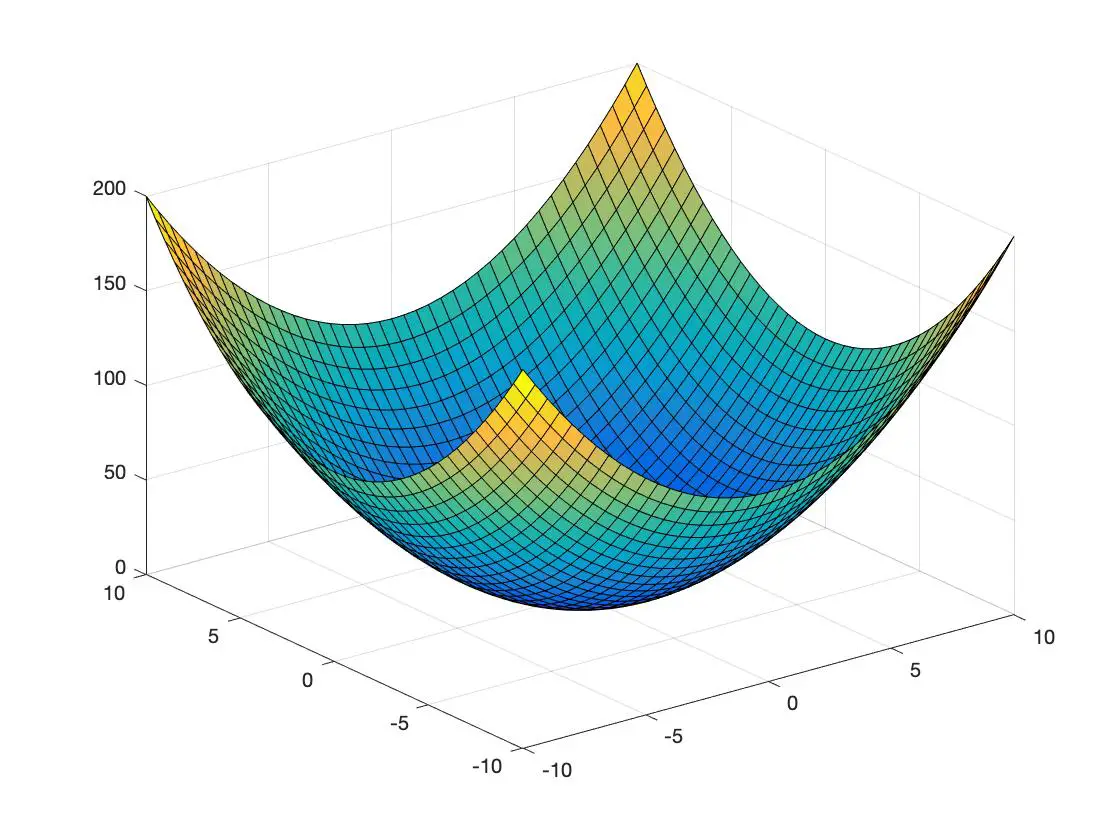
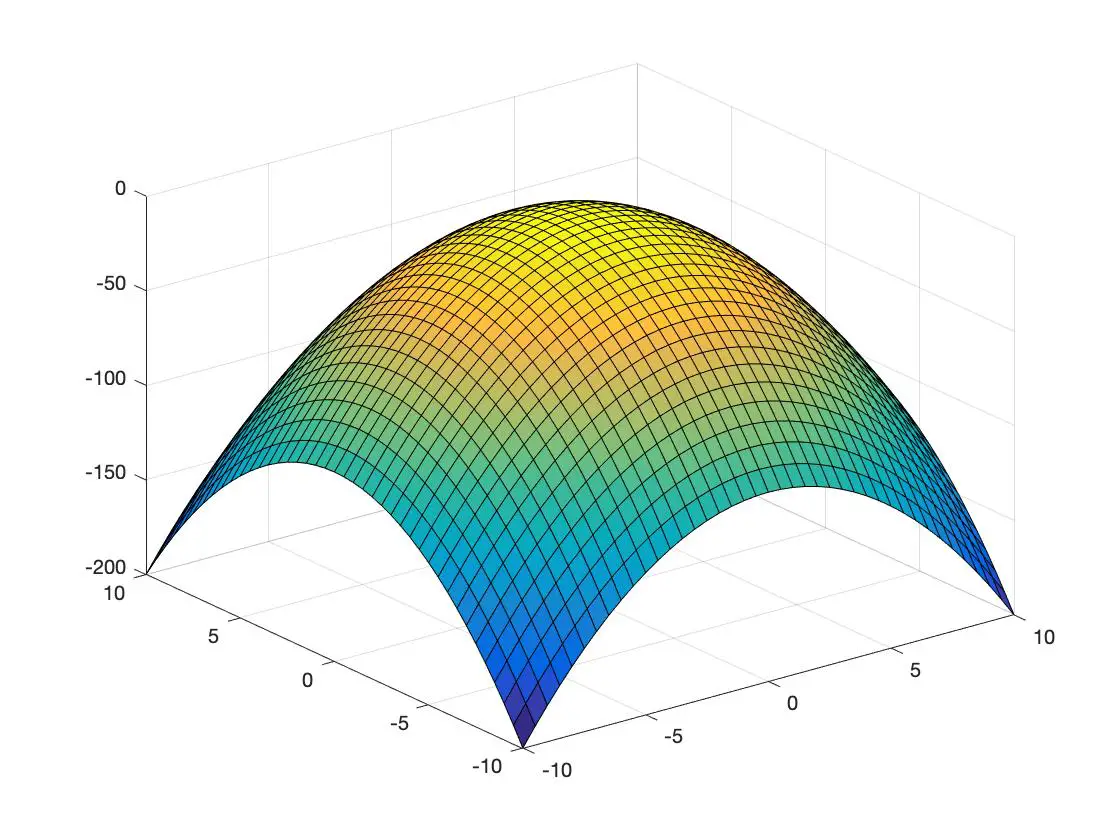
下面是一个在 3 维空间中表示的凸函数和另一个凹函数的示例：

凸函数

凹函数

图像的 ALT 属性为空；它的文件名是concavity-and-convexity-of-a-function-with-the-hessian-matrix-1024x768.jpg

Hessian矩阵的更多应用

Hessian 矩阵的主要用途是我们已经看到的，但是，它还有其他应用。我们在下面为最好奇的人解释它们。

泰勒多项式

2 个或更多变量函数在该点的泰勒多项式展开

$a$

像这样开始：

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

正如您所看到的，泰勒展开式的二阶项由在多项式展开点求值的 Hessian 矩阵给出。

带边框的粗麻布矩阵

Hessian矩阵的另一个用途是计算多元函数的最小值和最大值

$f(x,y)$

被限制为另一个角色

$g(x,y)$

。为了解决这个问题，使用有界Hessian矩阵，并遵循以下过程：

步骤1：计算拉格朗日函数，其定义如下：

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

步骤2：找到拉格朗日函数的临界点。为此，我们计算拉格朗日函数的梯度，将方程设置为 0 并求解方程。

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

步骤 3：对于我们找到的每个点，我们计算有界 Hessian，它由以下矩阵定义：

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

步骤 4：我们确定每个临界点是最大值还是最小值：

这将是函数的局部最大值
$f$

在功能限制下

$g$

如果在临界点评估的有界 Hessian 矩阵的最后nm （其中n是变量数， m是约束数）主次数具有从负号开始的交替符号。

这将是函数的局部最小值
$f$

在功能限制下

$g$

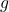
如果在临界点评估的尖锐 Hessian 矩阵的最后nm （其中n是变量数， m是约束数）主次数都具有负号。

应该记住，一个受约束函数相对于另一个受约束函数的相对最小值或最大值对于不受约束函数来说不一定如此。因此，有边界的 Hessian 矩阵仅对此类问题有用。

与其他业务的关系

最后，Hessian矩阵还与其他重要的运算或矩阵联系在一起，主要是与雅可比矩阵和与拉普拉斯算子。

与雅可比矩阵的关系

函数的 Hessian 矩阵

$f$

是同一函数梯度的雅可比矩阵：

$\displaystyle H_f = J(\nabla f)$

拉普拉斯算子

Hessian 矩阵迹等价于拉普拉斯算子：

$\displaystyle tr( H_f) = \Delta f$

这个等式很容易证明，因为拉普拉斯算子的定义是函数梯度的散度：

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

因此其表达式为：

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

而这个和只是Hessian矩阵的迹，因此等价性得到证明。

Hessian 矩阵（或 hesse）

什么是 Hessian 矩阵？

计算Hessian矩阵的示例

解决了 Hessian 矩阵的问题

练习1

练习2

练习3

练习4