两条线在空间中的相对位置

在这里您将找到空间中两条线的所有相对位置（在 R3 中）。此外，它还解释了如何使用两种可能的方法找到两条线之间的相对位置：通过范围或从每条线的点和向量。您甚至可以看到逐步解决的示例和练习。

两条线在空间中的相对位置是多少？

在解析几何中，当在三维空间（在 R3 中）中工作时，两条线之间有 4 种可能的相对位置：两条线可以是合并线、平行线、割线或割线。

平行线

如果两条线具有相同的方向但没有公共点，则它们是平行的。此外，平行线彼此之间的距离始终相同。

重合线

如果两条线具有相同的方向并且它们的所有点都是公共的，则它们重合。

相交线

两条相交线方向不同，但交于一点。

交叉线

两条相交线的方向不同，并且在任何一点都不相交。因此，两条交叉线不在同一平面上。例如，在线上方的图形表示中

$s$

总是走在前面

$r$

，所以他们永远不会互相接触。

有两种方法可以知道两条线之间的相对位置，因为它们取决于两条线的方程的表达方式：

如果线是矢量、参数或连续方程形式，最好从每条线的一个点和一个矢量计算相对位置（下面给出此方法的解释）。
另一方面，如果线以隐式（或一般）方程的形式定义，则通过计算两个矩阵的秩更容易知道两条线之间的相对位置（参见下面的解释）。

确定点和向量的两条线的相对位置

您可以通过一个点和每条线的向量找到两条线之间的相对位置。当直线以矢量方程、参数方程或连续方程的形式定义时，适合使用此方法。

因此，设方向向量和两条线上的任意点为：

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

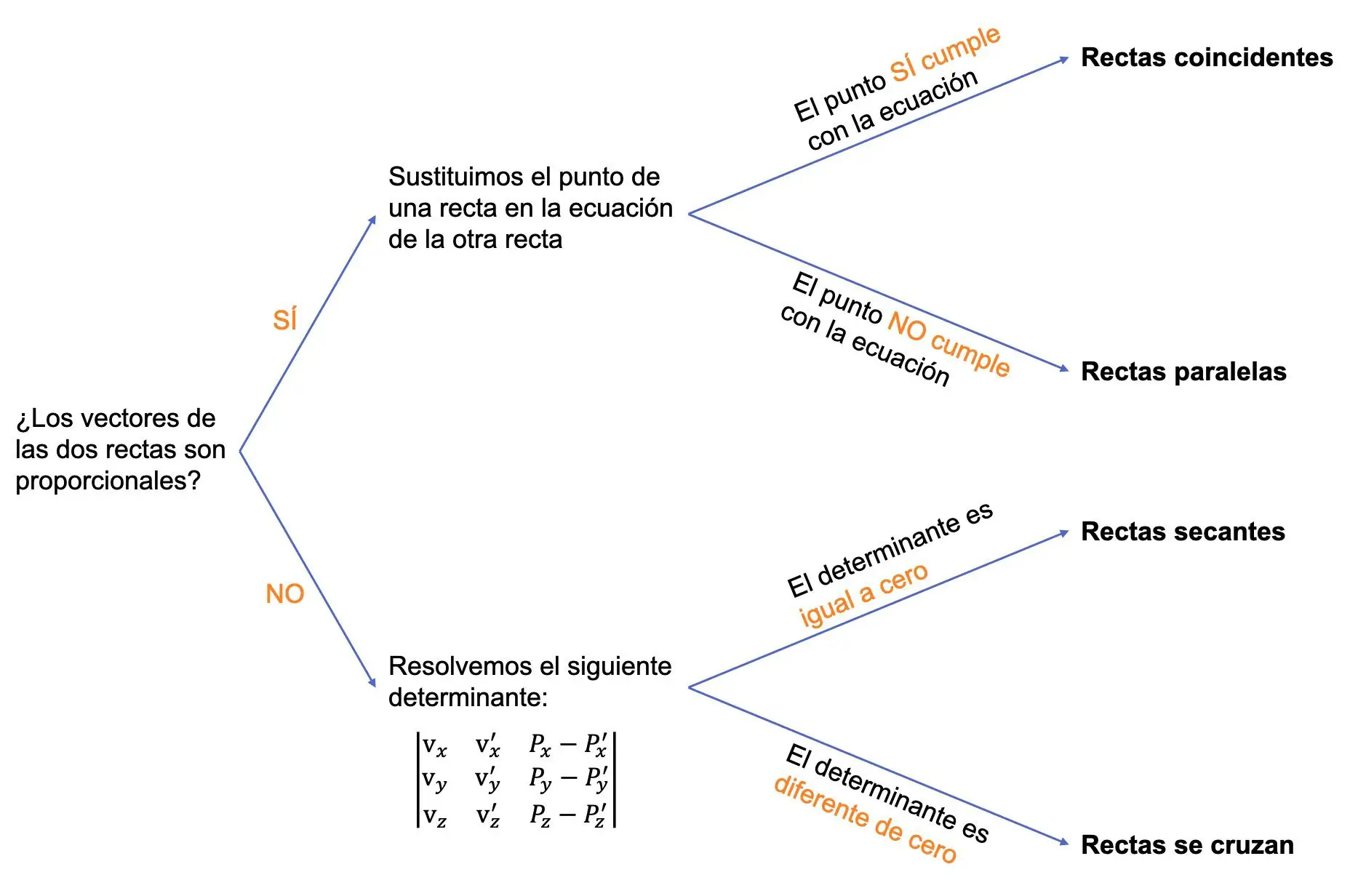
因此，要找到两条线的相对位置，我们需要遵循以下过程：

‣我们需要做的第一件事是查看两条线的向量是否成比例，并且根据情况，我们执行以下操作：

如果两个向量成比例，则两条线可以平行或重合。因此，我们必须检查一条直线的点是否满足另一条直线的方程：
- 如果一条直线的点满足另一条直线的方程，则意味着两条直线重合。
- 否则，这意味着两条线是平行的。
如果两个向量不成比例，则直线可能相交或相交。在这种情况下，我们必须求解以下 3×3 行列式：

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- 如果前一个行列式等于 0，则两条线相交于一点（它们相交）。
- 如果前一个行列式不为零，则两条线相交。

下图总结了整个过程：

确定两条线之间相对位置的示例

前面的过程可能看起来有点复杂，但是你可以看到它是相反的，我们将解决一个问题作为示例：

确定以下两条线之间的相对位置：

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

将两条直线表示为向量方程，其中每条直线的方向向量为：

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

每条线经过的点是：

$R(2,0,1)\qquad \qquad S(1,-3,1)$

一旦我们知道了一个点和每条线的方向向量，我们就应用上面的方法。首先，我们必须检查向量的坐标是否成比例：

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

由于两个向量不成正比，因此线只能相互接触或交叉。因此，我们现在需要求解由方向向量和每条线上的点形成的以下行列式：

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

我们将这些值代入公式：

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

我们计算行列式，为此您可以使用任何方法（Sarrus 规则、补集法或辅因子法等）：

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

如果确定的结果为零，则这意味着线交叉（它们接触）。但行列式不等于 0，因此两条线相交。

按行查找两行的相对位置

找到两行相对位置的另一种方法是计算两个具体矩阵的秩，我们将在接下来看到。当两条直线为隐式（或一般）方程形式时，此方法非常有用。

因此，如果我们有两条线用三维空间（在 R3 中）中的隐式（或一般）方程表示：

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

设 A 为两条线的系数组成的矩阵：

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

并给出扩展矩阵A’，它是两条线的所有参数形成的矩阵：

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

然后，根据前两个矩阵的范围，可以根据下表确定两行的相对位置：

因此，为了找到两行之间的相对位置，我们必须计算两个矩阵的秩，并且根据每个矩阵的秩，这将是一种情况或另一种情况。

这个定理可以使用 Rouché-Frobenius 定理（一种用于求解线性方程组的方法）来证明，但是在本页中我们不会进行证明，因为它相当麻烦并且没有增加太多内容。

如何按范围查找两条线的相对位置的示例

一旦我们了解了两行之间相对位置的理论，让我们通过一个例子看看它是如何付诸实践的：

找出以下两行的相对位置：

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

两条线是一般（或隐式）方程的形式，因此我们将使用秩的方法来找到两条线之间的相对位置。因此，我们用各行的系数构造矩阵 A 和扩展矩阵 A’：

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

一旦我们有了两个矩阵，我们就需要计算每个矩阵的秩。我们首先通过行列式计算矩阵 A 的秩：

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

矩阵 A 包含非零 3×3 子矩阵的行列式，因此矩阵 A 的秩为 3 。

现在我们计算扩展矩阵A’的范围。矩阵 A’ 始终至少处于矩阵 A 的秩，在本例中其值为 3，因此检查它是秩 4 还是秩 3 就足够了。为此，我们求解行列式4× 矩阵 4 的加法（或辅因子）：

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

整个扩展矩阵的行列式为零，因此矩阵 A’ 也是秩为 3 的。

因此矩阵 A 和矩阵 A’ 的秩为 3，因此两条线相交。也就是说，它们之间只有一个交点。

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

请记住，上面有一个表格，它根据矩阵 A 和 A’ 的范围总结了两条线之间相对位置的所有可能情况。

解决了空间中两条线之间的相对位置问题

练习1

找到以下两行之间的相对位置：

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

查看解决方案

由于两条线都表示为矢量方程，因此我们会从每条线的一点一矢量的方法求出两条线之间的相对位置。

每条线的方向向量为：

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

属于每条线的点是：

$R(3,4,0)\qquad \qquad S(1,-2,2)$

因此，要应用该过程，首先需要检查方向向量的分量是否成比例：

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

由于两个向量不成正比，因此直线只能相交或相交。因此，我们现在需要求解以下由方向向量和每条线上的点组成的行列式：

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

我们将这些值代入公式：

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

我们计算行列式：

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

判定器的结果等于 0，因此两条线相交。

练习2

计算以下两条线的相对位置：

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

查看解决方案

第一条线是参数方程的形式，第二条线是连续方程的形式，我们将通过每条线的点向量法确定两条线之间的相对位置。

右侧方向向量的坐标

$r$

是参数前面的系数

$t,$

以及线的方向向量的坐标

$s$

是分母的数字：

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

属于每条线的点是：

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

因此，要应用该过程，首先需要检查方向向量的分量是否成比例：

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

两个向量成正比，因此直线只能平行或重合。为了消除这个疑问，需要将直线上的点代入

$r$

在直线方程中

$s$

（反之亦然）看看它是否满足所述方程：

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

通过代入直线上的点，我们得到一个等式，使得一条直线上的点满足另一条直线上的方程，而且它们的方向向量成比例。因此，两条线重合。

练习3

找出以下两行的相对位置：

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

查看解决方案

两条线是一般（或隐含）方程形式，因此我们将使用排名方法来查找两条线之间的相对位置。因此，我们用各行的系数制作矩阵 A 和扩展矩阵 A’：

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

一旦我们有了两个矩阵，我们就需要计算每个矩阵的秩。我们首先通过行列式计算矩阵 A 的秩：

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

矩阵 A 的所有 3×3 行列式均为零，但矩阵内部有一个非零 2×2 行列式，因此矩阵 A 的秩为 2 。

现在我们计算扩展矩阵A’的范围。矩阵 A’ 总是至少是矩阵 A 的范围，在本例中为 2，因此有必要检查它是否有一个不取消的 3×3 行列式，以及该行列式的行列式是多少。整个矩阵：

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

扩展矩阵 A’ 确实包含 3×3 个非零子行列式，而且整个扩展矩阵的行列式等于 0，因此矩阵 A’ 的秩为 3 。

因此矩阵 A 的秩为 2，矩阵 A’ 的秩为 3，因此两条线是平行的。也就是说，它们没有任何共同点。

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

请记住，在方法的说明（上面）中，您有一个表格，根据矩阵 A 和 A’ 的等级总结了两条线之间相对位置的所有可能情况。

练习4

找出以下两行的相对位置：

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

查看解决方案

在这种情况下，两条线是笛卡尔（或隐式）方程形式，因此我们将使用排序方法来查找两条线之间的相对位置。因此，我们用各行的系数构造矩阵 A 和扩展矩阵 A’：

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

一旦我们知道了两个矩阵，我们就需要计算每个矩阵的秩。我们首先通过行列式计算矩阵 A 的秩：

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

矩阵 A 包含一个 3×3 子矩阵，其行列式非零，因此矩阵 A 的秩为 3 。

现在我们计算扩展矩阵A’的范围。矩阵 A’ 始终至少具有矩阵 A 的秩，在本例中其值为 3，因此检查它的秩是 4 还是 3 就足够了。为此，我们求解以下行列式由加法（或辅因子）组成的 4×4 矩阵的集合：

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$