相交线

在此页面上，您将找到有关割线的所有内容：它们的含义、存在的不同类型、如何知道两条线是否割线、如何找到它们的公共点……您还可以看到几个示例和已解决的练习的割线。

什么是两条相交线？

在数学中，割线的定义如下：

当两条线仅相交于一点时，它们就相交。因此，相交线只有一个公共点。此外，两条相交线必须包含在同一笛卡尔平面中。

两条线相交于一点的概念很重要，因为如果它们有多个交点，它们将是重合线，另一方面，如果它们没有交点，它们将是平行线。

相交线的示例

了解了两条相交线的含义后，现在让我们看一下此类线的两个不同示例：

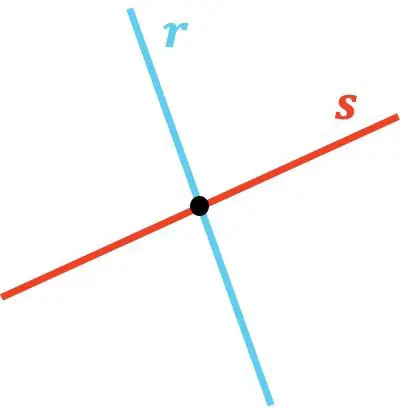
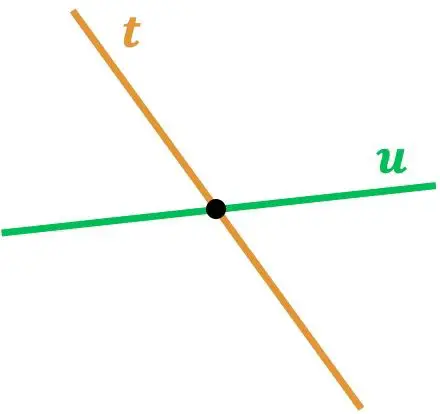
正如您所看到的，直线r和s相交，因为它们在一点相交。并且，以同样的方式，线t与线u相交，因为它们存在一个相交点。

相交线的类型

相交线有两种类型：

• 垂直线：以 90° 直角相交的线。
• 斜线：由以 0° 到 90° 之间的锐角相交的线组成（不包括在内）。

垂直直线

垂直线是相交形成四个 90 度角的线。

同样，两条垂直线的斜率始终满足以下条件：

垂直相交线的另一个属性是它们的方向向量（指示线方向的向量）之间的点积等于零。

如果您对垂直线更感兴趣，在此链接中您可以看到垂直线的示例。此外，您还将了解如何计算与另一条线垂直的线、此类线的属性、逐步解决的练习等。

斜线

斜线是成对相交形成锐角和钝角的线。也就是说，形成两个锐角（小于90°）和两个钝角（大于90°）。然而，根据两条线的角度的定义，两条线之间的角度是其形成的角度中最小的。

两条斜线与其斜率之间的角度可以使用以下公式计算：

如何知道两条线是否相交？

求两条线的相对位置主要有3种方法：

• 与两条线的方向向量。
• 随着两条线的斜率。
• 具有两条直线的隐式（或一般）方程。

然后我们将看到对已知两条线何时相交的 3 种方法的解释。

从线的方向向量

如果两条不同直线的方向向量（标记直线方向的向量）的坐标不成比例，则这两条直线相交。

让我们看看逐步解决两条相交线的练习：

两条线都表示为参数方程，因此每条线的方向向量的分量就是参数前面的数字

因此，要查看方向向量是否成比例，我们需要将它们的坐标分开。如果两个部分的结果相同，则它们将成比例；另一方面，如果结果不同，则意味着向量不成比例。

分量的划分不相等，因此矢量不成比例，因此线相交。

在斜坡的起点

如果两条线具有不同的斜率，则意味着两条线相交。

例如，以下两条线相交，因为它们具有不同的斜率：

线的斜率

为 -2 且直线的斜率

是 3。

由于两条线的斜率不同，因此它们相交。

由直线的隐式方程

还可以通过直线的隐式方程（或一般方程）求出两条直线是否相交。直线的隐式方程如下：

因此，当两条线的系数 A 和 B 不成比例时，两条线相交。

让我们看一下用隐式方程定义的两条相交线的示例：

为了验证这是两条相交线，我们必须分析系数A（变量前面的数字）的比例关系

）与系数B（变量前面的数字

）：

这两项不成比例，因此两条线实际上相交。

找到两条相交线的公共点

正如我们所见，相交线只有一个公共点。因此，要计算两条割线的交点，需要求解两条线组成的方程组。

例如，我们将找到以下两条线的交点：

为了确定两条线的交点，我们必须求解由两条线组成的线性方程组：

在这种情况下，我们将用代入法来求解系统。因此我们将隔离变量

将第一个方程代入第二个方程：

一旦我们知道未知的价值有多少

我们将其值代入找到的表达式中

因此，方程组的解就是两条线的交点。而这一点是

线与圆相交

通常，当我们说两条线相交时，我们指的是我们刚才看到的概念。然而，在几何中，割线还有另一种含义：

与圆相交的直线是在两个不同点与圆（或曲线）相交的直线。

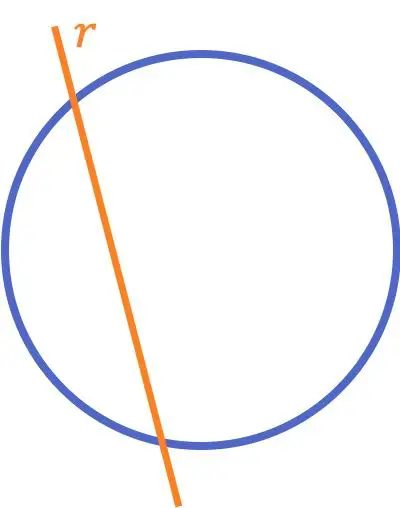
与小学中通常教授的两条相交线的概念不同，与圆相交的线的定义以及线与圆的所有相对位置经常在后面的课程中学习。