在这里您可以找到所有类型的直线方程的公式。此外,您将能够看到如何计算它们的示例,并通过直线方程的求解练习进行练习。
直线的所有方程是什么?
请记住,直线的数学定义是一组连续的点,这些点以相同的方向表示,没有曲线或角度。
因此,为了解析地表达平面(在 R2 中)中的任何直线,我们使用直线方程,并且为了找到它们,您只需要属于该直线的点和该直线的方向向量。仅用这两个几何元素,就可以求出该直线的所有不同方程,如下:
直线方程有矢量方程、参数方程、连续方程、隐式(或一般)方程、显式方程、点斜率方程和正则(或分段)方程。
所有类型的直线方程都有相同的目标:以数学方式表示直线。但该直线的每个方程都有其属性,因此,根据问题的不同,最好使用其中之一。

了解了直线方程的概念后,我们现在开始具体分析每种直线方程的特征。下面详细解释了该行中不同类型的方程,但如果您愿意,可以直接转到汇总表的末尾,其中包含该行中所有方程的公式。
直线的向量方程
是的
![]()
是直线的方向向量,
![]()
属于右边的点:
![]()
直线的矢量方程的公式为:
![]()
金子:
-

和

是线上任意点的笛卡尔坐标。
-

和

是构成线的一部分的已知点的坐标

-

和

是线的方向向量的分量

-

是一个标量(实数),其值取决于线上的每个点。
它是平面中直线的矢量方程,也就是说,当使用 2 个坐标(在 R2 中)的点和矢量时。然而,如果我们在空间中(在 R3 中)进行计算,我们就必须在直线方程中添加一个额外的分量:
![]()
直线的参数方程
直线的参数方程可由其矢量方程得到:
![]()
我们首先将参数相乘
![]()
由右边的方向向量:
![]()
接下来,我们添加 X 和 Y 坐标:
![]()
最后,分别清除每个变量,我们得到直线的参数方程:
![]()
金子:
-

和

是线上任意点的笛卡尔坐标。
-

和

是构成线的一部分的已知点的坐标

-

和

是线的方向向量的分量

-

是一个标量(实数),其值取决于线上的每个点。
和之前一样,这些是平面(R2)中直线的参数方程,但要找到空间(R3)中直线的参数方程,需要为第三个变量 Z 再添加一个方程:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e31f05449ce57a8af9ae4dda38535013_l3.png)
直线的连续方程
任何直线的连续方程都可以从其参数方程推导出来:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-708dbb33878e2bab0dcc94c84f6ab670_l3.png)
如果我们清除设置
![]()
从每个参数方程我们得到以下表达式:
![]()
![]()
E 通过使两个所得方程相等,我们得到直线的连续方程:
![]()
![]()
简而言之,直线的连续方程为:
![]()
金子:
-

和

是线上任意点的笛卡尔坐标。
-

和

是构成线的一部分的已知点的坐标

-

和

是线的方向向量的分量

该公式适用于二维(2D)下直线的连续方程。但如果我们在 3 维 (3D) 中执行运算,我们需要向直线方程添加一个附加组件:
![]()
直线的隐式或一般方程
是的
![]()
是直线的方向向量,
![]()
属于右边的点:
![]()
直线的隐式、一般或笛卡尔方程的公式为:
![]()
金子:
-

和

是线上任意点的笛卡尔坐标。
- 系数

是直线方向向量的第二个分量:

- 系数

是方向向量改变符号的第一个分量:

- 系数

通过替换已知点来计算

在直线方程中。
式中,直线的隐式方程也可以通过连续方程的分数相乘得到。
直线的显式方程
直线的显式方程的公式为:
![]()
金子:
-

是直线的斜率。
-

它的 y 轴截距,即与 Y 轴相交的高度。
在下面的部分中,您将看到如何确定参数
![]()
和
![]()
但是,特别是,找到显式方程的另一种方法是使用隐式方程;为此,必须解决未知的问题
![]()
的隐式方程。
参数m和n的含义
正如我们在直线的显式方程的定义中看到的,参数
![]()
是直线的斜率,
![]()
它的 y 轴截距。但是,这是什么意思?让我们从一条线的图形表示中看到这一点:

独立一词
![]()
是直线与计算机轴(OY 轴)的交点。例如,在上图中
![]()
等于 1,因为该线与 y 轴相交于 y=1。
另一方面,术语
![]()
表示线的斜率,即它的倾角。正如您在图表中看到的那样,
![]()
等于 2,因为 1 个水平单位,直线上升 2 个垂直单位。
显然,如果斜率为正,则函数增加(上升),反之,如果斜率为负,则函数下降(下降)。
计算直线的斜率
一旦我们确切地知道了直线的斜率是多少,我们就看看它是如何计算的。因此,有 3 种不同的方法可以用数值确定直线的斜率:
- 给定线上两个不同的点

和

直线的斜率等于:
- 是的

是直线的方向向量,其斜率为:
- 是的

是直线与横坐标轴(X 轴)形成的角度,直线的斜率等于该角度的正切:
![]()
![]()
![]()

直线的点斜率方程
直线的点斜率方程的公式为:
![]()
金子:
-

是直线的斜率。
-

是线上一点的坐标

直线的正则方程或分段方程
尽管直线方程的这种变体鲜为人知,但是可以从直线与笛卡尔轴的交点获得直线方程。
设与给定线的轴的两个交点为:
用 X 轴切割:
![]()
Y轴切割:
![]()
直线的正则方程的公式为:
![]()

在数学中,直线的正则方程也称为线段方程或对称方程。
另一方面,系数
![]()
和
![]()
它们也可以使用以下公式从直线的一般方程中找到:
![]()
![]()
所有直线方程(公式)
总之,这是一个表格,显示了该线的所有方程的公式:

直线方程计算示例
现在我们已经了解了直线方程的完整解释,让我们看看如何解决直线方程的典型问题:
- 求该点确定的直线的所有方程

和向量
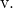
![]()
首先,我们从公式中求出直线的向量方程:
![]()
只需将点的坐标和向量代入公式即可:
![]()
其次,我们通过其对应的公式求出该直线的参数方程:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b4690a2ab033a4016f2d16b9554ddea_l3.png)
我们还确定了直线的连续方程,其公式为:
![]()
![]()
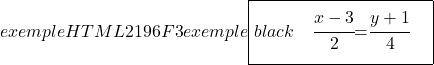
正如您所看到的,矢量、参数和连续方程很容易计算,您只需要使用它们各自的公式即可。
现在让我们继续寻找直线的一般(或隐式)方程。为此,我们将连续方程的两个分数相交:
![]()
![]()
![]()
![]()
现在我们可以确定未知数求解直线的显式方程
![]()
隐式方程的:
![]()
![]()
![]()
![]()
因此,直线的斜率等于 2(伴随自变量的项
![]()
)。
![]()
这样我们就可以计算出直线的点斜率方程,其公式为:
![]()
![]()
![]()
最后,为了找到直线的分段方程,我们计算其与 OX 和 OY 轴的交点,然后应用其公式:
![]()
与横坐标轴(X轴)的交点
![]()
![]()
![]()
![]()
![]()
与y轴的交点(Y轴)
![]()
![]()
![]()
![]()
![]()
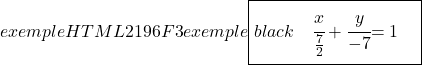
过两点的直线方程
直线方程中另一个非常常见的问题是找到由两个给定点确定的直线方程。虽然我们可以用两个点然后方程来计算直线的方向向量,但下面我们为您提供一个公式,您可以通过它直接轻松地找到该直线的方程。
考虑位于一条直线上的两个点:
![]()
从 2 个点求直线方程的公式为:
![]()
当给定直线经过的 2 个点时,这个公式允许我们直接计算直线的点斜率方程。
解决了直线方程的问题
练习1
求点定义的直线的矢量方程、参数方程和连续方程
![]()
及其指向向量
![]()
两者兼而有之:
![]()
首先,我们根据公式计算直线的矢量方程:
![]()
![]()
然后我们使用相应的公式找到该线的参数方程:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a734c32ae40ca816c19b895e54916eb4_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-bff16cf5ab85c87d8a866a2d74ea2a31_l3.png)
最后,我们用相应的公式确定直线的连续方程:
![]()
![]()
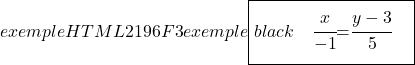
练习2
求该点确定的直线的隐式方程、显式方程和点斜率方程
![]()
其方向向量为
![]()
![]()
直线的隐式方程的公式为:
![]()
因此,我们必须找到系数 A、B 和 C。未知数 A 和 B 是从直线的方向向量的坐标中获得的,因为以下等式总是得到验证:
![]()
因此,系数 A 是向量的第二个坐标,系数 B 是向量改变符号的第一个坐标:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9357fbcba6acde824f0fa1cc3e389a0c_l3.png)
因此,我们只需要找到系数C即可。为此,我们必须将已知属于该直线的点代入其方程:
![]()
![]()
![]()
![]()
![]()
因此,该直线的隐式、一般或笛卡尔方程为:
![]()
现在我们可以确定未知数求解直线的显式方程
![]()
隐式方程的:
![]()
![]()
![]()
![]()
因此,直线的斜率等于 3(自变量之前的项)
![]()
)。
![]()
并且,根据直线的斜率值,我们可以计算出直线的点斜率方程,其公式为:
![]()
![]()
![]()
练习3
确定以下直线上的 3 个点,用隐式或一般方程表示:
![]()
要计算一条线上的点,我们只需为其中一个变量赋值,然后找到该点处另一个变量的值。
我们通过做计算第一个点
![]()
![]()
![]()
![]()
![]()
![]()
然后我们找到第二个点,为变量提供另一个值
![]()
例如
![]()
![]()
![]()
![]()
![]()
![]()
![]()
最后,我们通过求解计算第三点
![]()
![]()
![]()
![]()
![]()
![]()
![]()
练习4
求该点定义的直线的所有方程
![]()
和向量
![]()
![]()
首先,我们从公式中求出直线的向量方程:
![]()
![]()
其次,我们通过其对应的公式求出该直线的参数方程:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3bf46da9a68147118874a619f918077_l3.png)
我们还利用其公式确定了直线的连续方程:
![]()
![]()
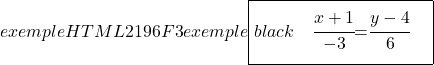
现在让我们继续寻找直线的隐式或一般方程。为此,我们将连续方程的两个分数相交:
![]()
![]()
![]()
![]()
现在我们可以确定未知数求解直线的显式方程
![]()
隐式方程的:
![]()
![]()
![]()
![]()
因此,直线的斜率等于 -2(伴随自变量的项
![]()
)。
![]()
这样我们就可以计算出直线的点斜率方程,其公式为:
![]()
![]()
![]()
最后,为了找到直线的分段方程,我们计算直线与 OX 和 OY 轴的交点,然后使用其公式:
![]()
与横坐标轴(X轴)的交点
![]()
![]()
![]()
![]()
![]()
与y轴的交点(Y轴)
![]()
![]()
![]()
![]()
![]()
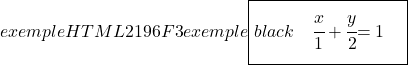
练习5
求通过以下两点的直线方程:
![]()
由于我们已经知道直线上的两个点,因此我们直接将直线方程的公式应用于两个给定点:
![]()
现在我们将这些点的笛卡尔坐标代入公式:
![]()
最后,我们计算直线的斜率:
![]()
![]()
因此,穿过这两点的直线方程为:
![]()