直线和平面的相对位置

10 7 月, 2023

在此页面上，您将找到直线和平面的相对位置。我们向您解释如何计算直线和平面之间的相对位置（2 种方法），此外，您将能够看到逐步解决的示例和练习。

直线和平面的相对位置是什么？

在查看直线和平面之间所有可能的相对位置之前，我们显然需要知道什么是直线，什么是平面。因此，如果您仍然不太清楚这两个概念，我们建议您首先查看详细解释的链接页面。

因此，在解析几何中，直线和平面之间在空间中仅存在三个相对位置：

线包含在平面中：当线包含在平面中时，这意味着它们有无数个公共点。
平行线和平面：直线和平面没有公共点时平行。
直线与平面相交：当直线与平面相交于一点时，直线与平面相交。所以他们只有一件事是共同的。

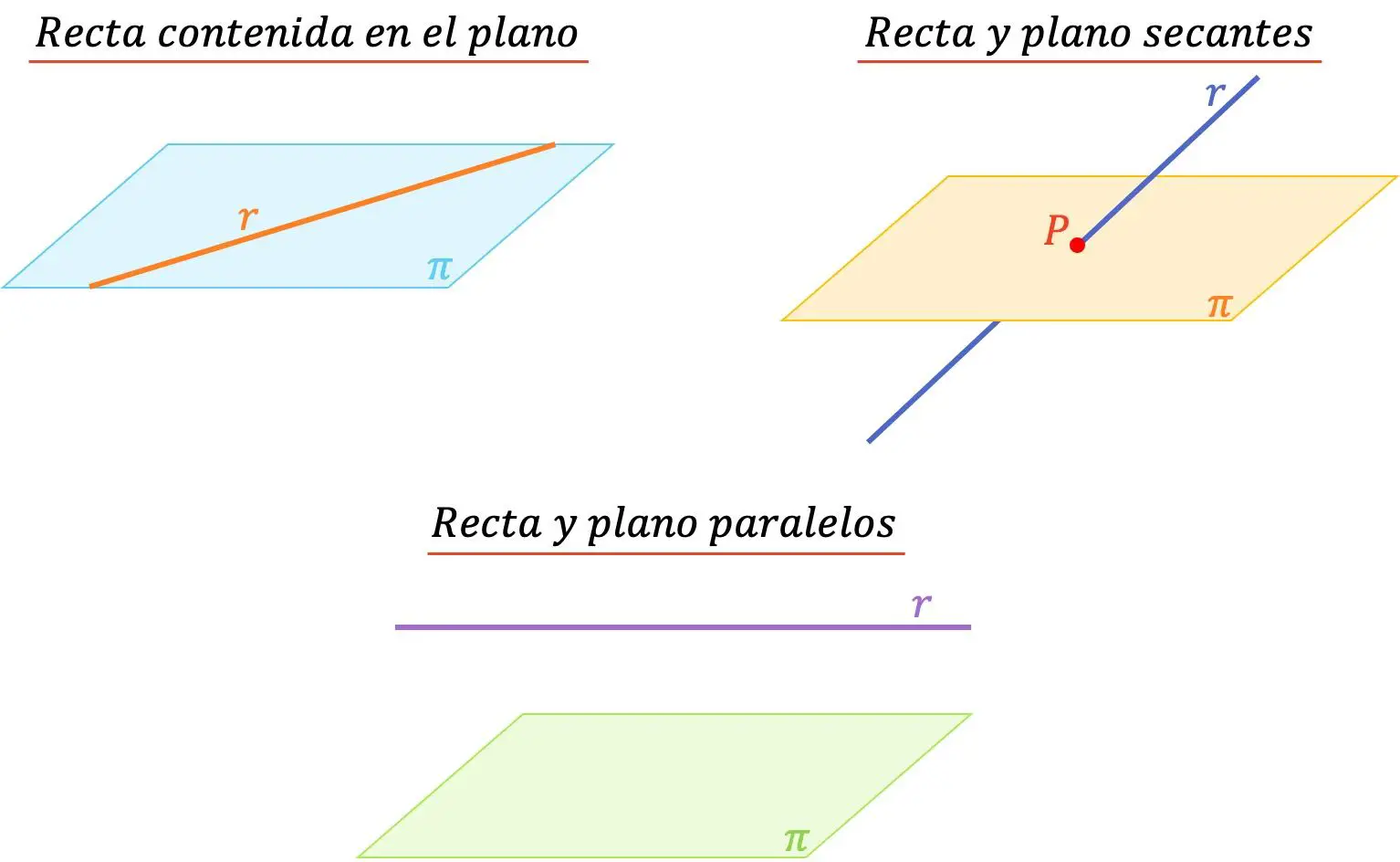
另一方面，当直线包含在平面内或它们彼此平行时，它们形成的角度将为 0°。另一方面，当直线和平面相交时，两个几何元素之间的角度可以在0°（不含）到90°（含）之间。

如何计算直线和平面的相对位置？

求直线和平面在空间中的相对位置主要有两种方法：通过范围或通过向量。

当直线表示为隐式（或一般）方程时，使用秩方法更容易。另一方面，如果直线是用另一种类型的方程给出的，例如当它是向量、参数或连续方程的形式时，使用向量方法会更快。

如果您不记得该直线的方程是什么样的，我们为您留下了一个页面，您可以在其中查阅该直线的所有方程。在这里，您将找到所有直线方程、快速求出经过两点的直线方程的公式、逐步求解的示例和练习。

因此，根据问题使用一种或另一种方法更为实用，因此我们建议您了解如何执行这两种过程。下面通过示例对这两种方法进行说明。

当直线是隐式（或一般）方程的形式时

确定直线和平面之间相对位置的一种方法是计算两个矩阵的秩。

如果该线由其隐式（或一般）方程定义：

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

并且该计划也用一般方程的形式表示：

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

我们将 A 称为由平面和直线方程的系数 A、B 和 C 组成的矩阵：

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

矩阵 A’ 将是包含两个方程的所有系数的展开矩阵：

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

那么，直线和平面之间的相对位置由前面两个矩阵的extent值根据下表确定：

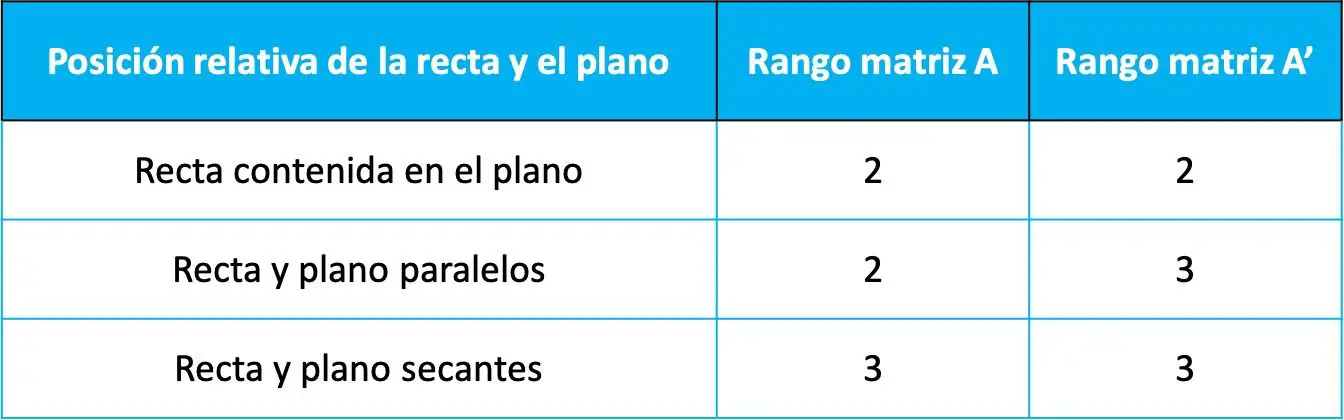
通过范围研究空间中直线和平面之间的相对位置

Rouche-Frobenius toerem（用于求解线性方程组的定理）可以证明相对位置取决于这两个矩阵的秩。不过，在本页中我们不会进行演示，因为没有必要了解它，而且它也没有提供太多内容。

如何通过范围查找直线和平面的相对位置的示例

为了让您能够准确地了解这是如何完成的，我们将解决一个练习作为示例：

研究跟随直线与跟随平面之间的相对位置：

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

该直线由两个相交平面定义，即表示为隐式方程。因此，我们将使用排序方法来研究直线和平面之间的相对位置。

首先要做的是用方程的系数构造矩阵 A 和扩展矩阵 A’：

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

现在我们需要计算每个矩阵的秩。我们首先通过行列式求出矩阵 A 的范围：

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

矩阵 A 的行列式为零，但它包含一个行列式不为零的 2×2 子矩阵，因此它是一个秩为 2 的矩阵。

另一方面，还需要计算矩阵A’的秩。并且扩展矩阵 A’ 的范围将始终至少与矩阵 A 的范围相同，因此我们只需要检查它是 3 阶还是 2 阶：

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

另一方面，扩展矩阵 A’ 确实有一个不同于 0 的 3×3 子行列式，因此它的秩为 3。

因此，由于矩阵 A 的秩为 2，矩阵 A’ 的秩为 3，因此直线和平面平行。

当直线是另一种方程的形式时

当直线用隐式方程以外的方程表示时，无论是向量方程、参数方程还是连续方程，最好使用我们下面解释的方法。

因此，如果直线以向量方程、参数方程或连续方程的形式给出，则意味着我们知道属于该直线的点及其方向向量。

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

另一方面，我们也知道平面的法向（或垂直）向量是多少：

$\vv{n} \perp \pi$

然后，根据这2个向量和直线上的点，可以计算出直线和平面之间的相对位置，如下所示：

如果直线的方向向量与平面法线向量之间的标量积不为零，则意味着直线与平面相割。

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
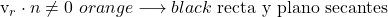
但如果直线的方向向量与平面法向向量之间的标量积等于零，则有两种可能：直线包含在平面内或它们平行。而要知道是哪种情况，我们必须将直线上一点的坐标代入平面方程中。
- 如果点满足平面方程，则直线包含在平面内。
- 另一方面，如果该点不满足平面方程，则直线和平面平行。

使用向量确定直线和平面的相对位置的示例

一旦我们了解了这种方法的理论，现在让我们看看逐步解决的练习：

求以下直线与以下平面之间的相对位置：

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

首先，将直线定义为参数方程，因此其方向向量和经过的点为：

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

另一方面，垂直于平面的矢量为：

$\vv{n} =(2,1,-2)$

一旦我们知道了直线的方向向量和垂直于平面的向量，我们就必须计算两者之间的标量积：

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

点积的结果为零，因此直线只能包含在平面内或与平面平行。因此，为了找出是哪种情况，我们将直线上的点的笛卡尔坐标代入平面的方程中：

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

通过将直线上的点代入平面方程中，我们得到一个等式，因此该点遵守平面方程，因此，直线包含在平面中。

发表评论取消回复