本页解释了直线和圆之间存在的不同相对位置。此外,您将能够了解如何找到直线和圆之间的相对位置。
直线和圆的相对位置是什么?
在解析几何中,直线相对于圆的相对位置只能是外线、相切或割线:
- 外部:当直线和圆心之间的距离大于半径时。
- 切线:当直线到圆心的距离等于半径时。
- 割线:当直线到圆心的距离小于半径时。
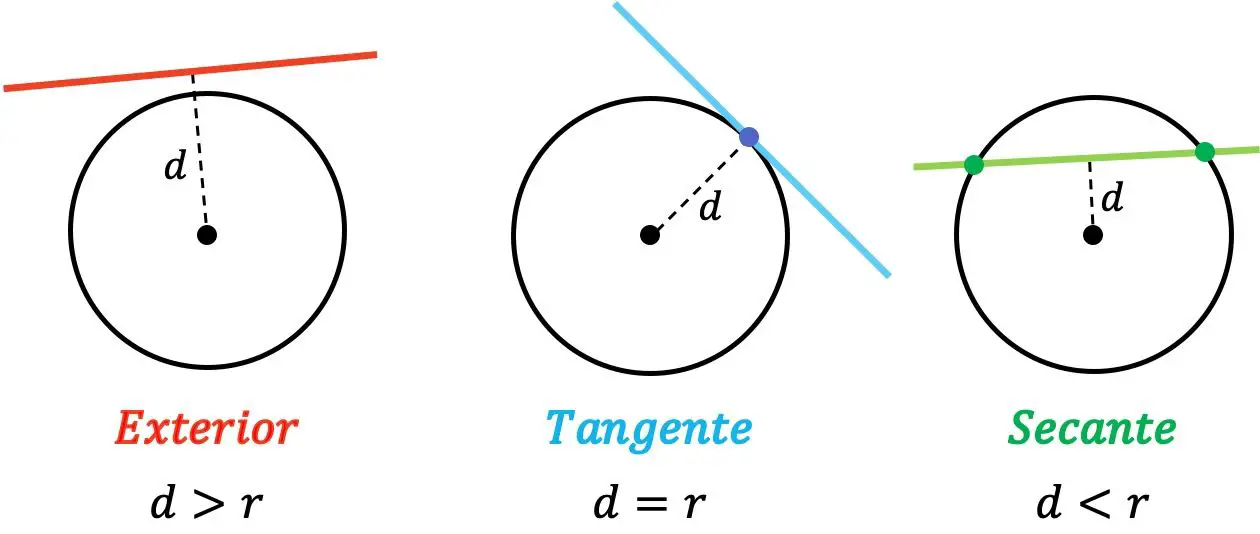
因此,如果一条线位于圆之外,则它不会在任何点与圆相交。另一方面,当直线与圆相切时,两者有一个共同点。最后,当一条线与圆相交于两个不同的点时,该线与圆相割。
如何确定直线和圆的相对位置?
求平面上直线相对于圆的相对位置有两种方法:一种是计算直线到圆心的距离,另一种是求解如下方程的复合方程组:直线和圆的方程。
接下来,我们将详细了解每种方法是什么。
方法一:直线到圆心的距离
正如我们在解释直线与圆的相对位置概念时看到的,直线与圆心之间的距离表明了它是什么类型的相对位置。
因此,该方法包括找到直线和圆心之间的距离。显然,为了能够做到这一点,您必须知道如何计算点和线之间的距离,在此页面上您可以看到如何做到这一点,以及示例和已解决的练习。
因此,根据获得的距离结果,会出现一种情况或另一种情况:
- 如果获得的距离大于圆的半径,则该线将在圆之外。
- 如果获得的距离等于圆的半径,则该线将与圆相切。
- 如果获得的距离小于圆的半径,则该线将与圆相交。
方法 2:求解方程组
查找直线与圆的相对位置的另一种方法是使用由直线方程和圆方程组成的方程组。显然,要应用此方法,您需要知道周长方程是什么以及直线方程的公式是什么。
根据方程组解的数量,我们将面临一种或另一种情况:
- 如果方程组无解,则说明直线和圆没有公共点,因此直线在圆外。
- 如果方程组有 1 个解,则意味着直线和圆有公共点,因此直线与圆相切。
- 如果方程组有 2 个解,则意味着直线和圆有两个公共点,因此直线与圆相割。