点与线之间的距离

在这里您将找到用于计算点和线之间距离的公式。此外，您将能够看到一些示例和已解决的点与线之间距离的练习，甚至该操作的应用程序（例如，计算平行线之间的距离）。

点与线之间的距离公式

点到线的距离是该点到线的最短距离。从数学上讲，这个最小距离相当于从该点到该线所画的垂直于该线的线段的长度。

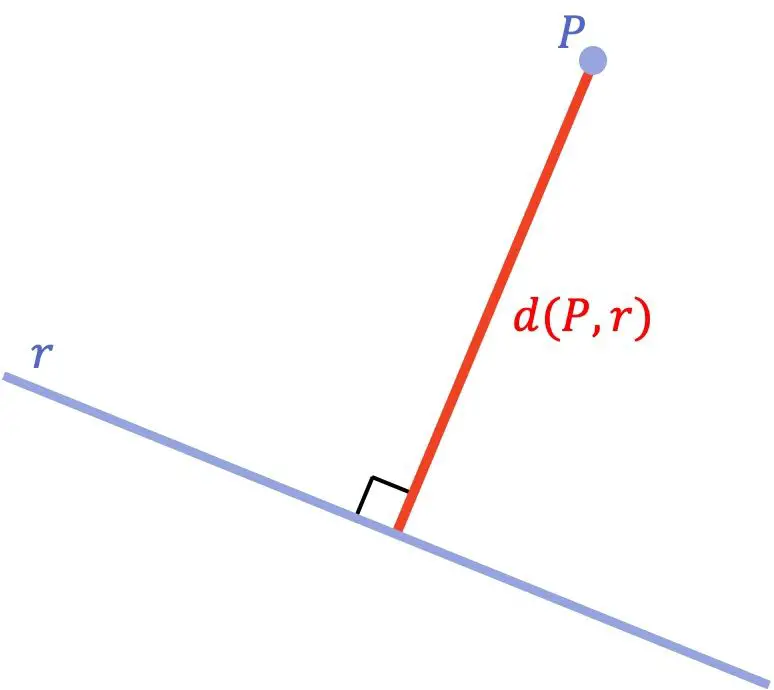
一旦我们了解了点和线之间的距离的几何概念，让我们看看用于计算所述距离的公式是什么：

给定直线的隐式（或一般）方程和平面上任意点的坐标：

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

点与线之间的距离的公式为：

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

重要提示：请注意，公式中直线的方程是隐式（或一般）方程的形式，因此，如果我们有以另一种类型的方程表示的直线，我们需要先将其传递给其隐式方程，然后再将其传递给隐式方程。我们可以应用这个公式。

计算点与线之间距离的示例

下面您可以看到计算点和线之间距离的示例：

找到点之间的距离
$P$

和法律

$r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

要计算点和线之间的距离，只需应用其公式：

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

现在我们用它的值替换每个项：

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

最后我们计算距离：

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

两条平行线之间的距离

计算线和点之间的距离的应用之一是找到平行线之间的距离。

显然，要理解我们下面将要解释的概念，您必须知道什么是平行线，因此，如果您不确切地知道它们的定义，我们会给您留下一个链接，我们将在其中详细解释它，您还可以看到示例的平行线。

要找到两条平行线之间的距离，只需在两条线上取一点并计算从该点到另一条线的距离即可。

因此，为了确定两条平行线之间的距离，还需要使用线与点之间的距离公式。

另一方面，如果使用公式时我们得到的距离为 0 个单位，则意味着这些线在某个点彼此接触，因此，这些线不是平行的，而是相交、重合或垂直的。如果您愿意，您可以在我们的网站上查看此类线路之间的差异。

那么我们通过一个例子来看看如何解决两条平行线之间的距离问题：

求下列两条平行线之间的距离：

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

我们需要做的第一件事是在一条线上（您想要的线）上得到一个点。在这种情况下，我们将计算线上的一个点

$s.$

为此，您必须为其中一个变量赋值，例如我们将这样做

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

现在我们清除另一个变量（

$y$

）得出的方程可以知道此时它的价值：

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

因此，从直线得到的点

$s$

东方：

$P(0,-2)$

一旦我们在一条线上有了一个点，我们就可以使用以下公式计算从该点到另一条线的距离：

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

解决了点与线之间的距离问题

练习1

计算点之间的距离

$P$

和法律

$r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

查看解决方案

要找到点和线之间的距离，只需应用其公式：

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

我们用它的值替换每一项并计算距离：

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

练习2

点之间的距离是多少

$P$

和法律

$r$

？

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

查看解决方案

在这种情况下，直线方程是隐式（或一般）形式。相反，要使用从点到直线的距离公式，该直线必须表示为隐式方程。因此，我们必须首先变换直线并将其传递给隐式方程（只需传递方程同一侧的所有项）：

$r: \ 3x+y-5=0$

一旦直线已经有了明确的形式，我们现在就可以使用点和直线之间的距离公式：

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

因此，我们将每一项替换为它的值并计算距离：

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

练习3

下面两条线之间的距离是多少？

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

查看解决方案

首先，我们将验证这是两条平行线。为此，变量的系数

$x$

和

$y$

必须彼此成比例，但不与独立项成比例：

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

事实上，这些线是平行的，因此我们可以应用该过程。

现在我们需要从其中一条线（您想要的线）中获取一个点。在这种情况下，我们将计算线上的一个点

$s.$

为此，您必须为其中一个变量赋值，例如我们将这样做

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

现在我们清除另一个变量（

$y$

) 得到的方程即可知道此时的值：

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

这样从直线上得到的点

$s$

东方：

$P(0,-1)$

一旦我们知道一条线上的点，我们就可以使用以下公式计算从该点到另一条线的距离：

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

练习4

计算未知数的值

$k$

使得点之间的距离

$P$

和法律

$r$

即5个单位。

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

查看解决方案

我们必须首先应用点和线之间的距离公式：

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

现在我们用它的值替换每一项并简化表达式：

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

问题陈述告诉我们点和线之间的距离必须等于 5，因此我们将前面的表达式等于 5：

$\cfrac{\lvert -49+k\rvert}{13}=5$

我们求解所得方程。分数的分子中存在绝对值，因此必须分别分析绝对值何时为正、何时为负：

$\cfrac{+(-49+k)}{13}=5$

$-49+k= 5 \cdot 13$

$-49+k= 65$

$k= 65+49$

$\bm{k= 114}$

$\cfrac{-(-49+k)}{13}=5$

$49-k= 5 \cdot 13$

$49-k= 65$

$49-65=k$

$\bm{-16=k}$

因此有两个可能的值

$k$

正确的：

$k=114$

任何一个

$k=-16.$