正切函数 - Mathority

在此页面上，您将找到有关正切函数的所有信息：它是什么、它的公式是什么、如何在图形中表示它、函数的特征、周期等。此外，您将能够看到正切函数的示例，以充分理解该概念。他甚至解释了正切定理以及正切函数与其他三角关系的关系。

正切函数公式

角度α的正切函数是一个三角函数，其公式定义为直角三角形（直角三角形）的对边与相邻（或相邻）分支之间的比率。

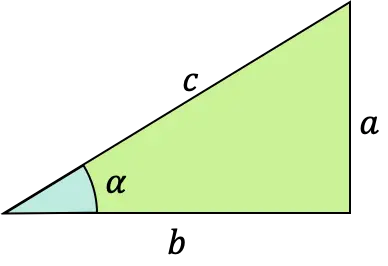
这种类型的数学函数也称为正切函数、正切函数或正切函数。它可以用缩写“tg”甚至“tan”来表示。

正切函数是三个最著名的三角函数之一，另外两个函数是角度的正弦和余弦。

正切函数的特征值

某些角度经常重复出现，因此可以方便地知道这些角度处的正切函数值：

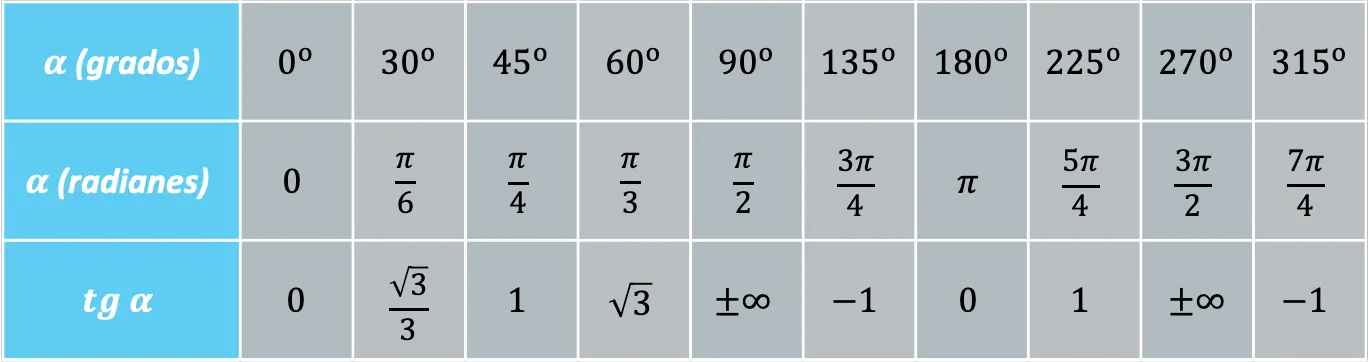
另一方面，正切函数可以通过以下基本三角恒等式与正弦和余弦函数联系起来：

$\text{tg } \alpha = \cfrac{\text{sen }\alpha}{\text{cos }\alpha}$

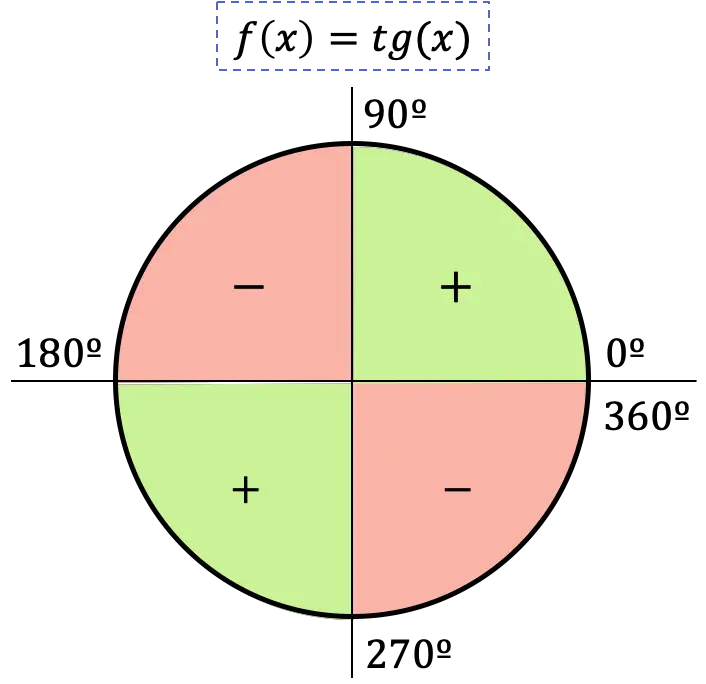
因此，正切函数的符号取决于角度所在的象限：

如果角度属于第一象限，则其正切将为正，因为在该象限中，正弦和余弦也是正的。
如果角度落在第二象限，则其正切将为负，因为在该象限中，正弦为正，余弦为负。
如果角度位于第三象限，则其正切将为正，因为在该象限中，正弦和余弦为负。
如果角度位于第四象限，则其正切将为负，因为在该象限中，正弦为负，余弦为正。

正切函数的图形表示

利用我们在上一节中看到的值表，我们可以绘制正切函数的图像。通过绘制正切函数的图形，我们得到：

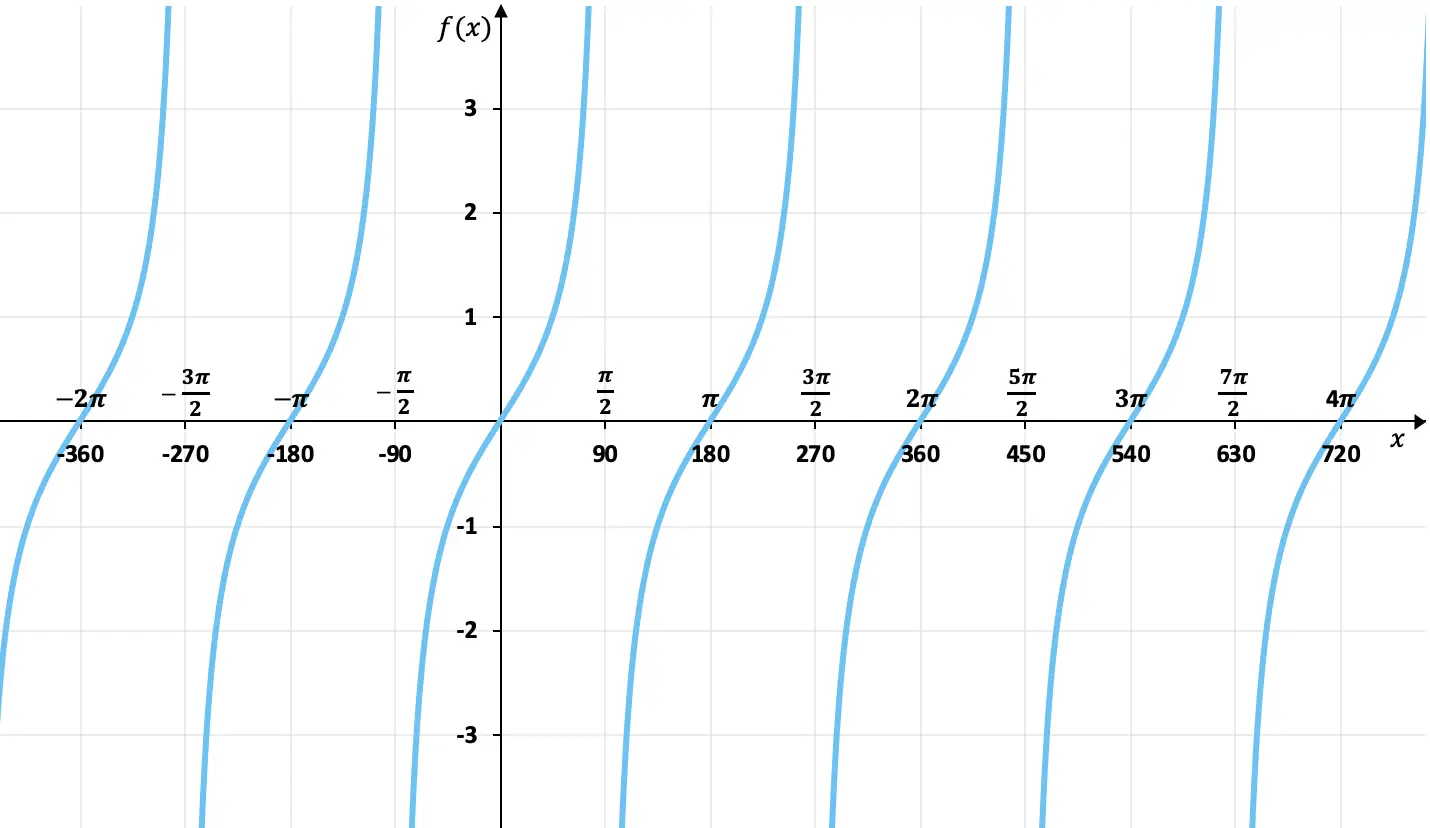
从图中可以看出，与正弦和余弦函数不同，正切函数的图像值没有界限。此外，这些值每 180 度（π 弧度）重复一次，因此它是周期为 180° 的周期函数。

另一方面，在该图中我们可以看到正切函数是奇数，因为它的相反元素具有相反的图像，或者换句话说，它关于原点（0,0）对称。例如，45° 的正切值为 1，-45° 的正切值为 -1。

最后，我们还可以看到正切函数有垂直渐近线。例如，它非常接近 x=90° 线，但从未触及它，并且每 180 度都会发生同样的情况。这意味着函数在这些点处的极限趋于无穷大。

正切函数的性质

正切函数具有以下特点：

正切函数的域是除存在垂直渐近线的点之外的所有实数：

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{(2k+1)\cdot \frac{\pi}{2} \right\} \qquad k \in \mathbb{Z}$

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{\ldots \ , \ -\frac{\pi}{2} \ , \ \frac{\pi}{2} \ , \ \frac{3\pi}{2} \ , \ \ldots \right\}$

正切函数的值域或值域都是实数。

$\text{Im } f= \mathbb{R}$

它是一个周期为 π 的连续奇函数。

$\displaystyle \text{tg}(-x) =- \text{tg }x$

此类三角函数与 y 轴（Y 轴）的单个交点位于点 (0,0)。

$(0,0)$

相反，它定期在 pi 的几个坐标处截取横坐标（X 轴）。

$\displaystyle (k\pi ,0) \qquad k \in \mathbb{Z}$

该函数在整个域上严格递增，因此它既没有最大值也没有最小值。

正切的导数为：

$f(x)=\text{tg } x \ \longrightarrow \ f'(x)= 1+\text{tg}^2 x=\cfrac{1}{\text{cos}^2 x} =\text{sec}^2 x$

最后，正切函数的积分为：

$\displaystyle \int \text{tg } x \ dx= -\ln \lvert \text{cos }x \rvert + C$

正切函数的周期

与其他三角函数（例如正弦和余弦）不同，正切函数没有大小，因为它既没有最大值也没有最小值。然而，它是一个周期函数，也就是说，它的值以我们在图形中看到的频率重复。

$\displaystyle f(x)= \text{tg}(wx)$

正切函数的周期是图形重复的两点之间的距离，由以下公式计算：

$\displaystyle \text{Periodo}=T=\cfrac{\pi}{w}$

正切定理

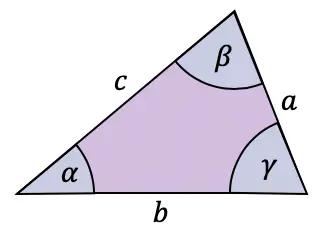
尽管正切公式通常用于直角三角形，但还有一个适用于任何类型三角形的定理：正切定理。

正切定理将任意三角形的边和角联系起来，如下所示：

$\displaystyle \cfrac{a+b}{a-b} = \cfrac{ \text{tg}\left(\frac{\alpha+\beta}{2}\right)}{\text{tg}\left(\frac{\alpha-\beta}{2}\right)}$

$\displaystyle \cfrac{a+c}{a-c} = \cfrac{ \text{tg}\left(\frac{\alpha+\gamma \vphantom{\beta}}{2}\right)}{\text{tg}\left(\frac{\alpha-\gamma\vphantom{\beta}}{2}\right)}$

$\displaystyle \cfrac{b+c}{b-c} = \cfrac{ \text{tg}\left(\frac{\beta+\gamma}{2}\right)}{\text{tg}\left(\frac{\beta-\gamma}{2}\right)}$

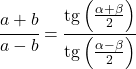
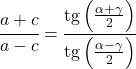
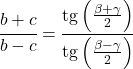
正切函数与其他三角比率的关系

下面是正切与三角学中最重要的三角比的关系。

与乳房的关系

角度的正切和正弦关系如下：

$\displaystyle \text{tg }\alpha = \pm \cfrac{\text{sen }\alpha }{\sqrt{1-\text{sen}^2\alpha \vphantom{\bigl( }}}$

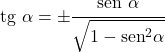
余弦比

同样，角度的正切和余弦与以下等式相关：

$\displaystyle \text{tg }\alpha = \pm \cfrac{\sqrt{1-\text{cos}^2\alpha \vphantom{\bigl( }} }{\text{cos }\alpha}$

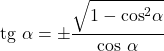
与余割的关系

虽然很难证明，但可以求解正切，使其仅取决于余割：

$\displaystyle \text{tg }\alpha = \pm \cfrac{1}{\sqrt{\text{csc}^2\alpha -1 \vphantom{\bigl( }}}$

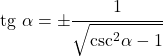
与割线的关系

角度的正切和割线由以下等式关联：

$\displaystyle \text{tg }\alpha = \pm\sqrt{\text{sec}^2\alpha -1$

与余切的关系

正切和余切是乘法逆元：

$\displaystyle \text{tg }\alpha =\pm \cfrac{1}{\text{cot }\alpha}$