在这里您将了解椭圆方程(公式)是如何计算的,无论是否以原点为中心。您还将了解椭圆的元素是什么、如何计算它们以及它们的用途。此外,您将能够看到椭圆方程的示例和已解答的练习。
椭圆方程公式
椭圆在直角坐标系中的方程公式为:
![]()
金子:
-

和

是椭圆中心的坐标:
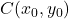
-

是椭圆的水平半径。
-

是椭圆的垂直半径。
以原点为中心的椭圆方程
一种非常常见的椭圆类型是其中心位于坐标原点,即点 (0,0) 的椭圆。这就是为什么我们将看到如何找到以原点为中心的椭圆方程。
遵循椭圆方程的公式:
![]()
如果椭圆以坐标原点为中心,则意味着
![]()
和
![]()
等于 0,所以你的等式将是:
![]()
有数学家也将这个表达式称为正则方程或椭圆的简化方程。
椭圆的元素
一旦我们看到了椭圆的方程是什么样子,我们就会看到它的元素是什么。但首先,让我们记住椭圆到底是什么:
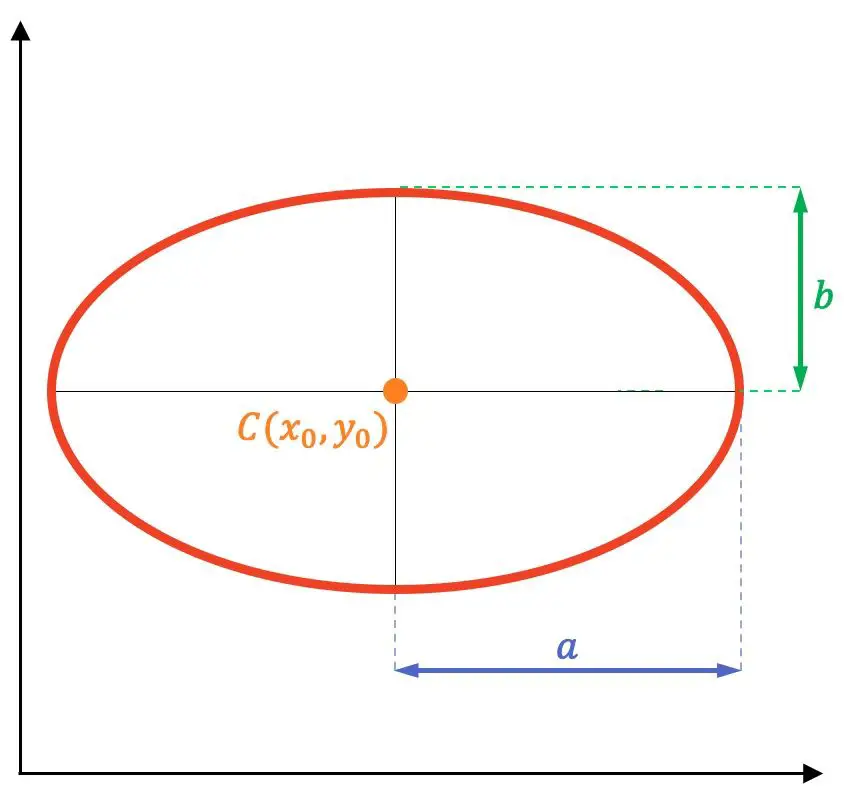
椭圆是一条平坦的、封闭的、与圆周非常相似的曲线,但它的形状更呈椭圆形。特别地,椭圆是平面上所有点的轨迹,该平面到其他两个固定点(称为焦点 F 和 F’)的距离之和是恒定的。
因此,椭圆的元素是:
- 焦点:这些是固定点 F 和 F’(下图中的紫色点)。椭圆上任意点与每个焦点之间的距离之和对于椭圆上的所有点都是恒定的。
- 主轴或焦轴:这是焦点所在椭圆的对称轴。也称为长轴。
- 次轴:这是垂直于主轴的椭圆的对称轴。它也称为短轴,对应于连接焦点的线段的垂直平分线。
- 中心:是椭圆轴的交点。此外,它是椭圆的对称中心(图形上的橙色点)。
- 顶点:椭圆与其对称轴的交点(黑点)。
- 半长轴或主轴:从椭圆中心到主轴顶点的线段。
- 半短轴或次轴:椭圆中心与次轴顶点之间的线段。
- 焦距:这是两个焦点之间的距离。
- 半焦距:对应于中心和每个焦点之间的距离。
- 无线电向量:是将椭圆的任意点连接到每个焦点的线段(图中的蓝色线段)。

椭圆各元素之间的关系
椭圆的不同元素彼此相连。此外,它们之间的关系对于椭圆的练习非常重要,因为它们通常是解决椭圆问题和确定其方程所必需的。
正如我们在上面椭圆的定义中看到的,椭圆上任意点到焦点 F 的距离加上该点到焦点 F’ 的距离是恒定的。这个常数值等于半长轴测量值的两倍。换句话说,以下等式对于椭圆上的任何点都成立:
![]()
金子
![]()
和
![]()
分别是点 P 到焦点 F 和 F’ 的距离,
![]()
是半焦轴的长度。
因此,由于次轴的顶点正好在焦轴的中间,因此它到其中一个焦点的距离等于半主轴的长度(
![]()
):
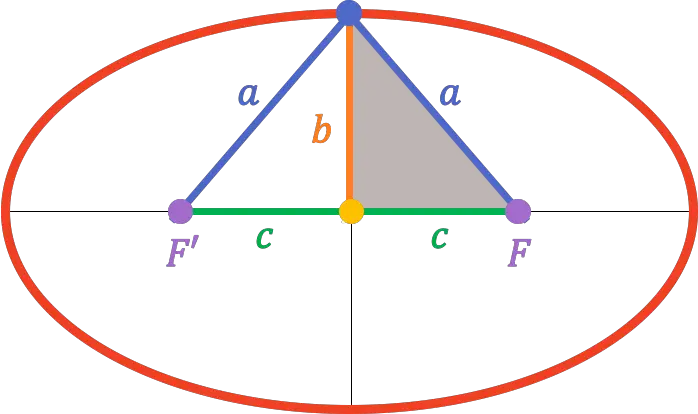
由此,根据毕达哥拉斯定理,可以找到主半轴、次半轴和半焦距之间的关系:
![]()
记住这个公式,因为它对于计算椭圆练习的结果非常有用。
椭圆偏心率
显然,并非所有椭圆都是一样的,但有些椭圆更拉长,有些则更扁平。因此,有一个系数用于测量给定椭圆的圆度。该系数称为偏心率,按以下公式计算:
![]()
金子
![]()
是从椭圆中心到其焦点之一的距离,
![]()
半长轴的长度。
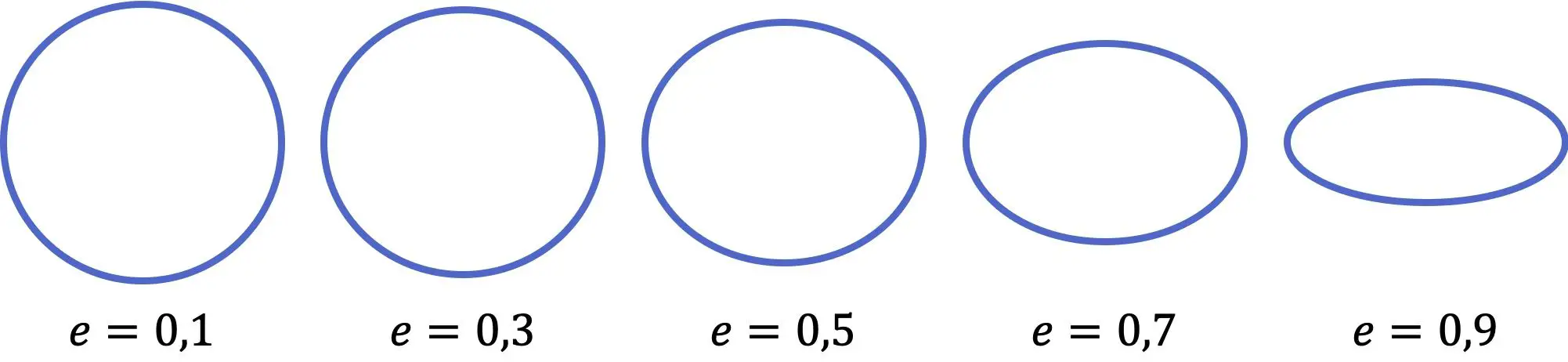
从前面的表示中可以看出,椭圆的偏心率值越小,它就越像圆形,反之,系数越大,椭圆就越扁平。此外,偏心率值的范围是从零(正圆)到一(水平线),两者都不包含在内。

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1C(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
最后,如果本文对您有用,您肯定也会对我们的双曲线公式和抛物线公式页面感兴趣。您将找到关于双曲线和抛物线是什么、它们的方程、它们的特征、示例、已解决的练习等的详细解释……