欧拉数是多少？ -Mathority

欧拉数（也称为欧拉常数）是数学各个领域中重要且必不可少的数学数，包括数论、拓扑、群论和函数论。它用希腊字母“e”表示，其近似值为2.71828。

数字 e 来自指数函数的公式，是复数论中的基本数。

它也是解决许多数学问题时出现的自然数，包括计算概率以及对增长和衰减过程进行建模。

欧拉数的由来是什么？

欧拉数以瑞士数学家莱昂哈德·欧拉（ Leonhard Euler ，1707-1783）的名字命名，他是有史以来最伟大的数学家之一，被认为是现代数学之父。

欧拉对数学的许多领域做出了宝贵的贡献，包括数论、几何、微积分、物理学和天文学。

他在对数的计算和理论著作中首先定义并使用了数 e （称为欧拉数）。欧拉的复数公式也是他对数学最显着的贡献之一。

这个值是怎么得到的呢？

事实上，计算欧拉数的方法有多种。然而，值得一提的是，这两种方法都没有给出准确的结果。因此，它的编号是连续的、无限的，但并不重复。

事实上，目前已知超过1万亿个数字组成了数字e。定义欧拉数的无穷级数是：

金子 ”！”是阶乘，它被定义为直到该数字的所有自然数的乘积。例如：

5！ = 5 4 3 2 1 = 120

我们可以将这个系列图形化地视为一系列高度为 1 且宽度递减的矩形的总和，其中每个矩形的宽度为 1/n!，其中 n 是阶乘的数量。

如果我们增加总和中的矩形数量，则指数函数曲线下面积的近似值会越来越接近欧拉数。

总之，欧拉数是无限级数之和的结果，是许多数学领域的基础。虽然它是一个无理数，但它的近似值为2.71828。

重要的是要记住，欧拉自己实现了这个方法来计算 e 到小数点后 18 位。

另一种计算方法：

我们可以使用一系列有限项来计算一条线上欧拉数的近似值。例如，如果我们采用上面定义的第一个无限级数：

我们可以通过添加级数的第一项来计算近似值。例如，如果我们添加前 6 项：

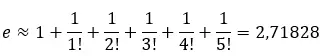
我们可以将该序列绘制在一条线上，看看它如何接近近似值2.71828 。

从图形上看，表示欧拉数的线可以绘制为一系列高度为 1、宽度递减的矩形，其中每个矩形的宽度为 1/n!，其中 n 是阶乘的数量。

如果我们增加总和中的矩形数量，则指数函数曲线下面积的近似值会越来越接近欧拉数。

具有欧拉数的指数方程

具有欧拉数的指数方程可用于对物理、生物学、经济学等科学中的各种现象进行建模。这里有些例子：

指数增长和衰退

该模型描述了人口增长或下降的速度，或有毒物质分解的速度。

例如，如果人口以每年 5% 的速度增长，则其规模可以用以下公式描述：

P(t) = P0 · e ^0.05t ，其中 P0 是初始种群规模。

放射性衰变模型

该模型描述了放射性原子随时间衰变的速率。

公式如下：

N(t) = N0 e ^-λt

其中 N0 是初始原子数，λ 是取决于放射性物质的常数，t 是时间。

这些只是如何在实践中使用具有欧拉数的指数方程的几个示例。指数方程在许多其他领域也是有用且相关的。

欧拉数有哪些应用？

欧拉数在数学和科学的不同领域有着广泛的应用。使用数字 e 的一些字段包括：

计算和数学分析：用于指数函数和对数函数的研究以及微分方程的求解。
数论——用于研究素数的分布和解决与数论相关的问题。
概率与统计：用于解决与概率分布和估计期望值相关的问题。
密码学——用于加密和解密算法的研究。
物理学——用于解决与热力学、量子力学和统计物理学相关的问题。
化学：用于解决与化学热力学和化学动力学相关的问题。

欧拉复数公式

欧拉复数公式建立了三角函数和指数函数之间的关系。公式写为：

其中“e”是自然对数的底数，“i”是虚数单位，“x”是实数，“cos”和“sin”分别是三角函数余弦和正弦。

这个公式在数学的许多领域都非常有用，包括数论、函数论和复杂性理论，并且在工程、物理和经济学中有广泛的应用。

其使用的一个实际示例是傅立叶分析中信号和系统的表示，其中周期信号被表示为复数正弦信号的总和。

欧拉公式用于描述这些复杂信号如何与描述各个正弦信号的实际三角函数相关。

欧拉数和复利

复利是一个金融概念，描述了一笔称为本金的资金通过随时间增加的利息赚取利息的过程。

换句话说，投资赚取的利息不仅来自初始资本，还来自前期赚取的利息。

欧拉数和复利相关，因为计算复利的公式使用欧拉数。复利的公式为：

A =^珀尔特

其中A是最终金额，P是本金，r是利率，t是时间，e是欧拉数。这样，欧拉数就成为计算复利的数学公式中的一个重要因素。

用具体数字计算复利的一个例子是：

假设我们有 1,000 欧元的投资，年利率为 5%，为期 2 年。计算复利的公式为：

A = P e ^rt = 1000 e ^{0.05 2} = 1000 1.1025 = €1102.5。

这意味着 2 年后，由于产生的复利，我们的初始资本 1,000 欧元将增加到 1,102.5 欧元。

欧拉数的数学练习示例

以下是涉及欧拉数的已解决数学问题的两个示例：

1. 求“e ^ix ”的值，其中 x 是实数：

欧拉恒等式告诉我们 e ^ix = cos(x) + i · sin(x)。因此，如果我们知道 x 的值，我们就可以使用三角函数计算 e ^ix的值。

2. 对于给定的 x 值计算 e^(x ² )：

我们可以使用泰勒级数来计算 e^(x ² ) 的值。 e ^x的泰勒级数是无限展开式，可以根据所使用的术语计算 e ^x值的逐次近似值。

如果我们用 x ²代替这个级数中的 x，我们就得到 e^(x ² ) 的泰勒级数。