您是否想知道有理数与其他数有何不同?在本文中,我们将深入探讨有理数,包括它们的独特特征和分类。准备好更好地理解这个概念!
什么是有理数?
有理数 (ℚ) 是实数的子类,包括所有可以表示为分数的数字。这意味着有理数可以写成两个整数之比a/b,其中 b ≠ 0。
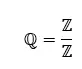
有理数也可以表示为重复的或有限的小数,因为它们是由一系列重复的数字组成的。有理数的一些例子有 1/2、3/4、10/3、2/3 和 π (pi)。
有理数子集
有理数可以分为两个子集:

实数集的另一个子类别是无理数,它稍微复杂一些。
有理数的例子
有理数是可以表示为分数的数,即两个整数的商。以下是有理数的一些示例:
-23
-4/5
-1/2
-7/9
所有代表整数的分数都是同样有理数的。例如:
-1/1
-2/2
-3/3
有理数的性质
有理数的主要特征是它们总是有一个非零分母。
该集合的第二个属性是每个有理数都可以由无穷多个等价分数表示。例如,有理数 3.5,等于 7/2,也可以写成 14/4、28/8……以及无穷多个其他分数。
有理数也满足分配律。这意味着将一个分数乘以或除以另一个分数不会影响结果:
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
有理数的表示
有理数可以用多种方式表示,但最常见的是分数。分数由两个数字组成:分子和分母。
分子表示整体中有多少个部分,分母表示整体中有多少个相等的部分。例如,如果将一块蛋糕分成八等份,并且其中三片被吃掉,则表示所吃蛋糕数量的分数将为 3/8。
表示有理数的另一种方法是用小数。小数是分数的简写方式,其中分母是数字 10、100、1000 等。例如,如果您有 1/4 的馅饼,则可以表示为 0.25(表示“0 个整体和 25/100”)。
不过,如果我们想用图形来表示它们,我们也可以将它们写在数轴上,这样可以很好地看出数字的顺序。接下来,我们向您展示这一行的示例:
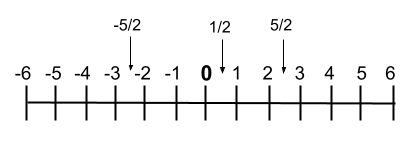
理性经营
有理数的基本运算与整数相同:加、减、乘、除。如果您想了解如何解决此类运算,我们建议您阅读有关分数运算的文章。
但是,如果您使用的是带十进制的有理数,则必须遵循处理十进制值时使用的求解运算过程。
有理数集的结论
经过详尽的解释,我们可以得出结论,有理数集是数学中最重要的数集之一。它包含所有可以表示为分数的数字,这使我们能够非常精确地表达数量。