最小二乘法是一种用于寻找与一组点相对应的最佳直线的数学工具。我们用简单的方式向您解释:
想象一下,图表上有一堆点分散在各处。你想要找到一条最“适合”这些点的直线,从而最小化线和点之间的距离。这就是最小二乘法背后的思想。
该方法使用公式来计算使点与线之间的差的平方和最小化的线的方程。也就是说,它寻找与点“偏差”最小的线。
简单来说,最小二乘法可用于分析调查过程中获得的数据,目的是以线性方式表达他们的行为,减少被盗信息的错误。
最小二乘法是谁发明的?
最小二乘法是统计学和数据分析的基本工具,由德国数学家卡尔·弗里德里希·高斯于 1794 年提出,但高斯直到1809 年才发表。
有趣的是,法国数学家安德里安·玛丽·勒让德 (Andrien-Marie Legendre) 在 1805 年独立开发了类似的版本。
两位数学家帮助创建了这种方法,该方法已广泛应用于各个学科,以将模型拟合到观测数据并做出准确的预测。
最小二乘公式
毫无疑问,要理解这个方法涉及到什么,有必要解释一下它的公式和实现过程。下面是最小二乘公式的详细解释:
定义问题
假设您有一个包含两个变量的数据集,一个自变量 (x) 和一个因变量 (y),并且您希望对该数据拟合一条直线。
目标是找到直线方程的系数值(截距和斜率),使 y 的实际值与预测值之间的差值平方和最小化拟合线。
计算直线方程
直线方程的形式为 y = mx + b,其中 m 是斜率,b 是 y 截距。计算myb值的最小二乘公式为:
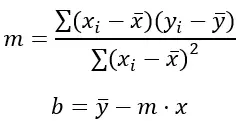
金子:
Σ 表示值的总和。
x i和y i分别是每个数据点的变量x和y的值。
x̄ 和 ş 分别是 x 和 y 值的平均值。
( xi – x̄) 和 (y i – ş) 是 x 和 y 的值及其各自均值之间的差。
( xi – x̄) 2是 x 值与其平均值之差的平方。
解释结果
使用公式计算出 m 和 b 的值后,您可以使用它们来获得拟合线的方程。例如,如果 m = 2 且 b = 3,则拟合线的方程将为 y = 2x + 3。这使您可以对不同 x 值的 y 值进行预测或估计基于调整后的权利。
什么时候使用最小二乘法?
您可能会问自己,什么时候使用这种方法?在各种情况下都非常有用!例如,当您想要分析实验或研究数据以查找关系或趋势时。
假设您正在调查房屋价格与其面积(平方米)之间的关系。您可以使用最小二乘法来找到最适合数据的直线,并让您清楚地了解这种关系。
它还在经济学中用于建模和预测产品需求或价格行为等变量。此外,在工程中,最小二乘法用于将数学模型拟合到测试或模拟数据。
最小二乘法是一种强大且多功能的工具,可用于许多研究和工作领域来分析数据并发现重要关系。
最小二乘法在其他定理中的应用
除了其本身的用途之外,最小二乘法在其他定理中也非常有用。下面让我们详细了解一下这个主题。
回归定理
它广泛用于回归定理中,以找到适合一组数据的最佳直线。例如,您可以使用它来分析植物的高度与其接收到的光量之间的关系,以确定植物在不同光照条件下的生长情况。
定理插值
在这种情况下,最小二乘法也应用于插值定理中,以找到最适合一组点的多项式函数。例如,您可以使用它根据位置和时间数据来近似移动物体的轨迹。
曲线拟合定理
它在曲线拟合定理中用于查找拟合一组数据的曲线。这在诸如气候数据建模以预测气候变化或预测射弹轨迹等应用中非常有用。
傅立叶分析定理
在傅里叶分析定理中,最小二乘法用于从一系列离散数据中逼近周期函数。这适用于数据信令以及图像和声音压缩。
非线性回归定理
最后,最小二乘法还应用于非线性回归定理中,以找到拟合不遵循线性关系的数据集的最佳曲线。例如,您可以使用它来分析化学物质的浓度如何影响反应速率。
最小二乘法示例
为了更好地理解如何应用最小二乘法,让我们看一下下面的示例。
假设您有以下植物在不同星期的高度数据(以厘米为单位):
| 星期 | 高度(厘米) |
| 1 | 十 |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | 二十 |
您想要找到适合该数据的最佳直线来预测未来的植物高度。
第 1 步:绘制数据图表
首先要做的是将数据绘制在散点图上。 x 轴代表周,y 轴代表高度(以厘米为单位)。这是图表:
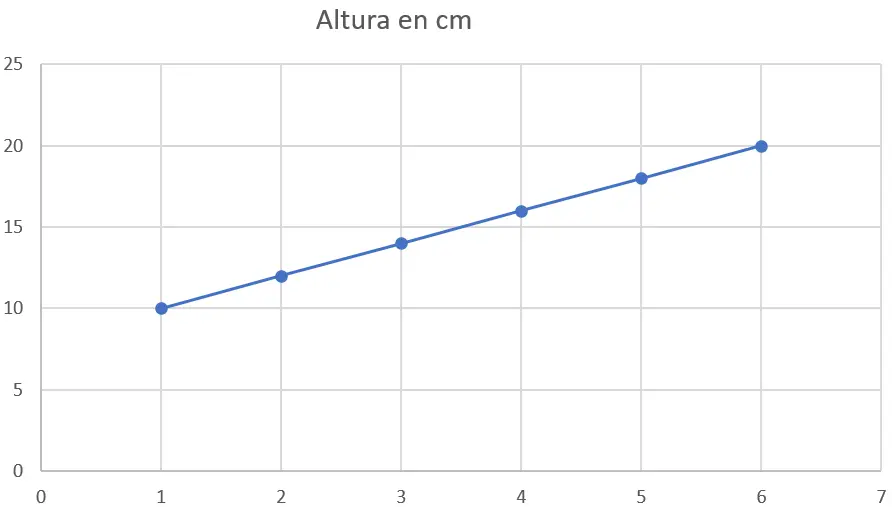
步骤 2 :应用最小二乘法
最小二乘法寻求找到一条线,使实际数据与线预测值之间的差值平方和最小。在这种情况下,直线由直线方程表示:y = mx + b,其中“y”是高度,“x”是周数,“m”是直线的斜率,“b”是y 轴截距。
为了找到使差值平方和最小的“m”和“b”的值,使用以下公式:
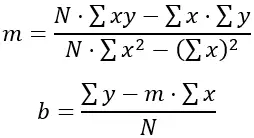
其中 N 是数据点的数量(在本例中为 6),Σxy 是周的总和乘以身高,Σx 是周的总和,Σy 是身高的总和,Σx 2是周的平方和。
将这些公式应用于高度数据,我们得到:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
将这些值代入“m”和“b”的公式中:
m = (6·630 – 21·90) ÷ (6·91 – 21 2 ) ≈ 2.07
b = (90 – 2.07 · 21) ÷ 6 ≈ 3.24
因此,高度数据对应的直线方程为:y。