优化问题——

这里我们解释一下函数优化问题是如何分阶段解决的。此外，您还可以通过解决优化问题的练习进行练习。

什么是优化问题？

优化问题是必须找到函数的最大值或最小值的问题。例如，优化问题涉及计算定义公司利润的函数的最大值。

如何解决优化问题

解决功能优化问题的步骤：

设置需要优化的功能。
推导出要优化的函数。
找到要优化的函数的关键点。为此，您需要将函数的导数设置为零并求解所得方程。
研究函数的单调性并确定函数的最大值或最小值。

优化问题的示例

考虑到优化问题的理论，我们将逐步解决此类问题，以便您可以看到它们是如何进行的。

在所有边长为 10 厘米的直角三角形中，计算表面积最大的一个的尺寸。

为了解决这个问题，我们将三角形的一个分支称为x ，另一分支称为y ：

步骤1：设置要优化的功能。

我们希望三角形的面积最大，三角形面积的公式为：

$A = \cfrac{b \cdot h}{2}$

在我们的例子中，三角形的底是x ，高度是 y 。然而：

$A = \cfrac{x \cdot y}{2}$

我们已经有了要优化的函数，但它依赖于两个变量，而它只能依赖于一个变量。然而，声明告诉我们两条腿的总长度必须为10厘米。然而：

$x+ y = 10$

我们从这个方程中解出y ：

$y = 10 -x$

我们将表达式代入函数：

$A = \cfrac{x \cdot y}{2} \ \xrightarrow{ y \ = \ 10 -x } \ A = \cfrac{x(10-x)}{2}$

$A(x) = \cfrac{10x-x^2}{2}$

现在我们有了计划的优化函数，它只依赖于一个变量，所以我们可以继续下一步。

步骤2：计算待优化函数的导数。

它是一个有理函数，因此我们应用除法导数公式来推导它：

$A(x) = \cfrac{10x-x^2}{2} \ \longrightarrow \ A'(x) = \cfrac{(10-2x) \cdot 2 - (10x-x^2) \cdot 0}{2^2}$

$A'(x) = \cfrac{20-4x}{4}$

第三步：找到关键点。

为了找到函数的临界点，我们需要将导数设置为零并求解所得方程：

$A'(x) = 0$

$\cfrac{20-4x}{4} =0$

4 整除左侧，因此我们可以通过乘以整个右侧来乘以它：

$20-4x=0 \cdot 4$

$20-4x=0$

$-4x=-20$

$x=\cfrac{-20}{-4}$

$x=5$

步骤4：研究函数的单调性并确定函数的最大值或最小值。

为了研究函数的单调性，我们表示在右侧找到的临界点：

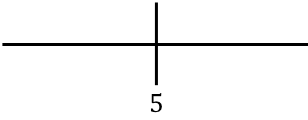
现在我们评估每个区间内导数的符号，以确定函数是递增还是递减。为此，我们在每个区间中取一个点（而不是临界点）并查看导数在该点的符号：

$A'(x) = \cfrac{20-4x}{4}$

$A'(0) = \cfrac{20-4\cdot0}{4} = \cfrac{20}{4} = 5 \ \rightarrow \ \bm{+}$

$A'(6) = \cfrac{20-4\cdot6}{4} = \cfrac{20-24}{4} = \cfrac{-4}{4} = -1 \ \rightarrow \ \bm{-}$

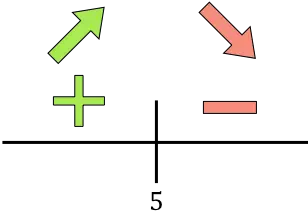
如果导数为正，则表示函数在增，如果导数为负，则表示函数在减。因此，函数增减的区间为：

生长：

$\bm{(-\infty, 5)}$

减少：

$\bm{(5,+\infty)}$

当 x=5 时，函数从增加变为减少，因此x=5 是要优化的函数的相对最大值。

因此，x=5是三角形面积最大的分支的值。简单计算另一条腿的价值：

$y = 10 -x \ \xrightarrow{x \ = \ 5} \ y = 10-5= \bm{5}$

总之，使三角形最大面积最大化的值为：

$\bm{x=5} \ \mathbf{cm}$

$\bm{y=5} \ \mathbf{cm}$

优化问题已解决

问题1

该药是给病人的，并且

$t$

几个小时后，活性成分的血液浓度由函数给出

$c(t) = te^{−t/2}$

毫克每毫升。确定最大值

$c(t)$

并指示何时达到所述值。

查看解决方案

步骤1：设置要优化的功能。

在这个问题中，他们已经给了我们建议的函数，即

$\displaystyle c(t) = t e^{-t/2} .$

步骤2：计算待优化函数的导数。

该函数由 2 个函数的乘积组成。因此，要计算函数的导数，我们必须应用乘积导数的规则：

$\displaystyle c'(t)=1 \cdot e^{-t/2} + t \cdot e^{-t/2} \cdot \left( \frac{-t}{2} \right)'= e^{-t/2} + t e^{-t/2} \cdot \frac{-1}{2}$

$c'(t)=e^{-t/2} + \cfrac{-1}{2}t e^{-t/2}$

第三步：找到关键点。

为了找到函数的临界点，我们求解

$c'(t)=0:$

$c'(t)=0$

$\displaystyle e^{-t/2} + \frac{-1}{2}t e^{-t/2}=0$

我们取公因数来求解方程：

$\displaystyle e^{-t/2} \left(1 - \frac{1}{2}t \right) = 0$

为了使乘法等于 0，乘法的两个元素之一必须为零。因此，我们将每个因子设置为0：

$\displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}$

一个数与另一个数相乘永远不会得到 0，因此，

$e^{-t/2}=0$

没有解决办法。

步骤4：研究函数的单调性并确定函数的最大值或最小值。

为了研究函数的单调性，我们表示在右侧找到的临界点：

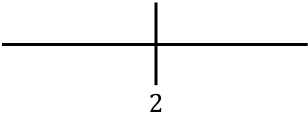
现在我们评估每个区间内导数的符号，以确定函数是递增还是递减。因此，我们在每个区间取一个点（不是临界点），并查看此时导数的符号：

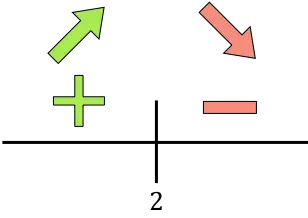
$\displaystyle c'(0)=e^{-0/2} + \frac{-1}{2}\cdot 0 \cdot e^{-0/2} = e^0 +\frac{-1}{2}\cdot 0 \cdot e^{0} = 1 + 0 = 1 \ \rightarrow \ \bm{+}$

$\displaystyle c'(3)=e^{-3/2} + \frac{-1}{2}(3)e^{-3/2} = 0,22-0,33 = -0,11 \ \rightarrow \ \bm{-}$

如果导数为正，则表示函数增大，反之，如果导数为负，则表示函数减小。因此待优化函数的增长和下降区间为：

生长：

$\bm{(-\infty,2)}$

减少：

$\bm{(2,+\infty)}$

该函数在 t=2 时从增加变为减少，因此t=2 是该函数的最大值。因此将在t=2小时内达到最大浓度。

最后，将最大值出现的值代入原函数，求得最大浓度值：

$c(2) = 2 \cdot e^{-2/2} = 2\cdot e^{-1} = 2 \cdot 0,37 = \bm{0,74} \ \mathbf{mg/ml}$

问题2

一家商店希望以每辆 1,000 欧元的价格出售 40 辆电动滑板车。但根据市场研究，滑板车价格每降低 50 欧元，最畅销的前 10 名滑板车的销量就会增加。

首先根据踏板车原价 1,000 美元降低 50 美元的次数编写商店的收入函数。接下来，确定获得最大利润的滑板车价格以及在该价格下获得的收入。

查看解决方案

步骤1：设置要优化的功能。

问题陈述给了我们一个线索，因为它告诉我们该函数必须取决于初始价格减少 50 美元的次数。因此，我们将价格降低 50 欧元的次数称为 x：

$x= \text{N\'umero de veces que se rebaja el precio 50}$

欧元

收入函数将是售出的踏板车数量乘以每辆踏板车的价格：

$I(x)= \text{N\'umero patintetes vendidos} \cdot \text{Precio de cada patinete}$

售出的踏板车数量将为 40 辆，每降价 50 欧元即可售出 10 辆踏板车。然而：

$\text{N\'umero patintetes vendidos} = 40 + 10x$

每辆踏板车的起始价格为 1000 欧元，每次降价将降低 50 欧元。然而：

$\text{Precio de cada patinete} = 1000 -50x$

因此，优化问题的函数是：

$I(x)= \text{N\'umero patintetes vendidos} \cdot \text{Precio de cada patinete}$

$I(x)= (40 + 10x) \cdot (1000-50x)$

$I(x)= 40000-2000x+10000x-500x^2$

$I(x)= -500x^2+8000x+40000$

步骤2：计算待优化函数的导数。

作为多项式函数，导数更容易计算：

$I(x)= -500x^2+8000x+40000\ \longrightarrow \ I'(x)= -1000x+8000$

第三步：找出函数的临界点。

为了找到函数的临界点，我们求解

$I'(x)=0:$

$I'(x)=0$

$-1000x+8000=0$

$-1000x=-8000$

$x=\cfrac{-8000}{-1000} = 8$

步骤4：研究函数的单调性并确定函数的最大值或最小值。

为了研究函数的单调性，我们将计算出的临界点表示在数轴上：

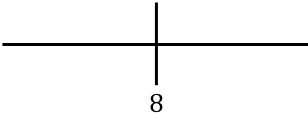
现在我们评估每个区间内导数的符号，以确定函数是递增还是递减。因此，我们在每个区间取一个点（不是临界点），并查看此时导数的符号：

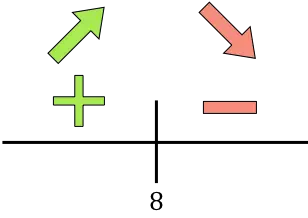
$I'(0)= -1000\cdot 0+8000=8000 \ \rightarrow \ \bm{+}$

$I'(10)= -1000\cdot 10+8000=-2000 \ \rightarrow \ \bm{-}$

如果导数为正，则表示函数在增，如果导数为负，则表示函数在减。因此，增长区间和下降区间为：

生长：

$\bm{(-\infty,8)}$

减少：

$\bm{(8,+\infty)}$

该函数在 x=8 处从增加变为减少，因此x=8 是该函数的最大值。因此，减少 50 欧元的 8 倍即可获得最大收入。

现在我们将最大收入出现的值代入原函数，求出最大收入的值：

$I(x)= -500x^2+8000x+40000$

$I(8)= -500\cdot 8^2+8000\cdot 8+40000 = \bm{72000}$

欧元

享受 50 欧元折扣 8 次后，每辆踏板车的价格为：

$\text{Precio de cada patinete} = 1000 -50x$

$\text{Precio de cada patinete} = 1000 -50\cdot 8=\bm{600}$

欧元

问题3

公司的成本函数（以千欧元为单位）可以使用以下表达式确定：

$f(x)=40-6x+x^2, \quad x \ge 0$

金子

$x$

代表给定产品生产的数千个单位。

确定必须生产多少才能使成本最小，该成本是多少，以及如果不生产这些物品，成本是多少。

查看解决方案

步骤1：设置要优化的功能。

问题陈述已经给我们提供了需要优化的函数，即

$\displaystyle f(x)=40-6x+x^2 .$

步骤2：计算待优化函数的导数。

$f(x)=40-6x+x^2 \ \longrightarrow \ f'(x)=-6+2x$

第三步：找到关键点。

为了找到函数的临界点，我们求解

$f'(x)=0:$

$f'(x)=0$

$-6+2x=0$

$2x=6$

$x=\cfrac{6}{2} = 3$

步骤4：研究函数的单调性并确定函数的最大值或最小值。

我们表示在右侧找到的临界点：

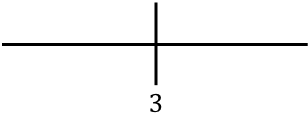
现在我们评估每个区间内导数的符号，以确定函数是递增还是递减。因此，我们在每个区间取一个点（不是临界点），并查看此时导数的符号：

$f'(0)=-6+2\cdot 0=-6\ \rightarrow \ \bm{-}$

$f'(4)=-6+2\cdot 4=-6+8=2\ \rightarrow \ \bm{+}$

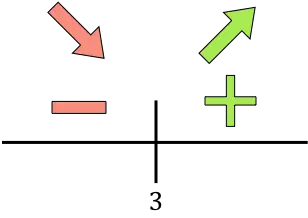
如果导数大于零，则函数在此区间内增加。另一方面，如果导数小于零，则函数在此区间内减小。因此，函数的增加和减少的区间为：

生长：

$\bm{(3,+\infty)}$

减少：

$\bm{(-\infty,3)}$

在 x=3 处，函数从递减变为递增，因此x=3 是函数的最小值。因此，生产3000台即可实现最低成本。

现在我们将达到最小成本的值代入原始函数来找到最小成本值：

$f(3)=40-6\cdot 3+3^2=\bm{31}$

数百万欧元。

另一方面，他们问我们，如果什么都不生产，成本是多少，也就是说，什么时候

$x= 0 .$

因此需要计算

$f(0):$

$f(0)=40-6\cdot 0+0^2= \bm{40}$

数百万欧元。

问题4

我们想要建造一个矩形木框架，其面积为 2 m ² 。我们知道，水平边的木材价格为 7.5 欧元/米，垂直边的木材价格为 12.5 欧元/米。确定矩形必须具有的尺寸，以使框架的总成本尽可能最小，并且所述成本也最小。

查看解决方案

步骤1：设置要优化的功能。

为了解决这个问题，我们将水平边称为x ，将垂直边称为y ：

购买水平边的费用为 7.5 欧元，购买垂直边的费用为 12.5 欧元。此外，对于每个框架，我们需要两个水平边和两个垂直边。因此，框架的成本可以通过以下函数确定：

$C(x,y)= 7,5\cdot 2x+12,5 \cdot 2y = 15x +25y$

我们已经有了优化的功能。但当它只能取决于一个变量时，它取决于两个变量。然而，声明告诉我们框架的表面积必须为2 m ² 。然而：

$x \cdot y = 2$

我们删除变量y ：

$y =\cfrac{2}{x}$

我们替换在要优化的函数中找到的表达式：

$C(x,y)= 15x +25y\ \xrightarrow{y \ = \ \frac{2}{x} } \ C(x)= 15x+25\left(\cfrac{2}{x} \right)$

$C(x)= 15x+\cfrac{50}{x} =15x +50x^{-1}$

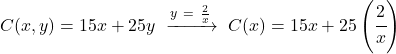
步骤2：计算待优化函数的导数。

$C(x)=15x +50x^{-1} \ \longrightarrow \ C'(x)=15 -50x^{-2}$

第三步：找到关键点。

为了找到函数的临界点，我们求解

$C'(x)=0:$

$C'(x)=0$

$15 -50x^{-2}=0$

$15 =50x^{-2}$

$15=\cfrac{50}{x^2}$

$\cfrac{15}{1}=\cfrac{50}{x^2}$

我们横向相乘来求解分数方程：

$15 \cdot x^2 = 50 \cdot 1$

$x^2 = \cfrac{50}{15}$

$x^2 = 3,33$

$\sqrt{x^2} = \sqrt{3,33}$

$x = 1,83$

步骤4：研究函数的单调性并确定函数的最大值或最小值。

我们将找到的临界点表示为在线分析函数的单调性：

现在我们评估每个区间内导数的符号，以确定函数是递增还是递减。因此，我们在每个区间取一个点（不是临界点），并查看此时导数的符号：

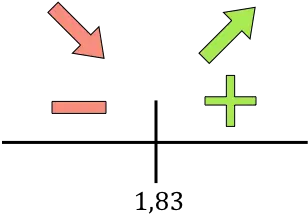
$f'(1)=15 -50\cdot 1^{-2} = 15-50 = -35 \ \rightarrow \ \bm{-}$

$f'(2)=15 -50\cdot 2^{-2} = 15-12,5 = 2,5 \ \rightarrow \ \bm{+}$

如果导数为正，则表示函数在增，如果导数为负，则表示函数在减。因此，增长区间和下降区间为：

生长：

$\bm{(1,83,+\infty)}$

减少：

$\bm{(-\infty,1,83)}$

在 x=1.83 处，函数从递减变为递增，因此x=1.83 是函数的最小值。

因此，x=1.83 是代表最小成本的水平边的值。现在我们来计算垂直边的值：

$y =\cfrac{2}{x} \ \longrightarrow \ y =\cfrac{2}{1,83} = \bm{1,09}$

因此，构成最小框架成本的值为：

水平边

$= x = \bm{1,83} \ \mathbf{m}$

垂直边

$= y = \bm{1,09} \ \mathbf{m}$

而这些值达到的最小成本是：

$C= 15\cdot 1,83+25\cdot 1,09=\bm{54,70}$

欧元

问题5

大教堂的门是由两根柱子支撑的半圆周拱门组成，如下图所示：

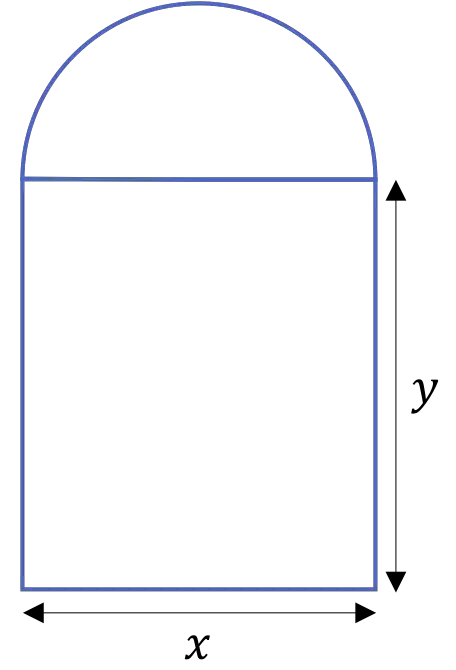
如果门的周长为 20 m，请确定尺寸

$x$

和

$y$

这最大化了整个门的表面积。

查看解决方案

步骤1：设置要优化的功能。

圆的面积用公式计算

$\pi r^2.$

所以整个门的面积将是矩形的面积加上圆周面积的一半：

$A(x,y)= x\cdot y + \cfrac{1}{2} \left[ \pi r ^2 \right]$

$A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]$

$A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]$

$A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]$

$A(x,y)= xy +\cfrac{\pi x^2}{8}$

我们已经有了优化的功能。但当它只能取决于一个变量时，它取决于两个变量。

不过，发布的消息告诉我们，整个大门的周长为20m。圆的周长用以下公式计算

$2 \pi r.$

因此，整个门的周长为：

$P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }$

周长必须为 20 m。因此，我们将前面的表达式设置为等于 20 来查找之间的关系

$x$

和

$y :$

$x+2y + \cfrac{ \pi x }{2 } = 20$

我们将所有项乘以 2 以消除分数：

$2\cdot x+2\cdot 2y + 2 \cdot \cfrac{ \pi x }{2 } = 2 \cdot 20$

$2x+4y + \pi x = 40$

我们清除

$y :$

$4y = 40-2x- \pi x$

$y = \cfrac{40-2x- \pi x}{4}$

我们替换在要优化的函数中找到的表达式：

$A(x,y)= x y +\cfrac{\pi x^2}{8}\ \xrightarrow{y \ = \ \frac{40-2x- \pi x}{4} }$

$A(x)= x \cdot \cfrac{40-2x- \pi x}{4}+\cfrac{\pi x^2}{8}$

$A(x)= \cfrac{40x-2x^2-\pi x^2}{4}+\cfrac{\pi x^2}{8}$

步骤2：计算待优化函数的导数。

$A'(x)=\cfrac{(40-4x-2\pi x)\cdot 4 +(40x-2x^2- \pi x^2)\cdot 0 }{4^2} +\cfrac{2\pi x \cdot 8 + \pi x^2 \cdot 0}{8^2}$

$A'(x)=\cfrac{160-16x-8\pi x }{16} +\cfrac{16\pi x}{64}$

第三步：找到关键点。

为了找到函数的临界点，我们求解

$A'(x)=0:$

$A'(x)=0$

$\cfrac{160-16x-8\pi x }{16} +\cfrac{16\pi x}{64} = 0$

这是一个带有分数的方程，因此我们将每一项乘以分母的 lcm 以消除分数：

$64 \cdot \cfrac{160-16x-8\pi x }{16} +64 \cdot \cfrac{16\pi x}{64} = 0$

$4\cdot ( 160-16x-8\pi x) +1\cdot 16\pi x= 0$

$640-64x -32 \pi x +16\pi x= 0$

$-64x -32 \pi x +16\pi x= -640$

$-64x -16 \pi x = -640$

$(-64 -16 \pi) x = -640$

$x=\cfrac{-640}{-64 -16 \pi} = 5,6$

步骤4：研究函数的单调性并确定函数的最大值或最小值。

为了研究函数的单调性，我们表示在右侧找到的临界点：

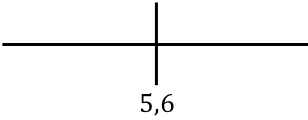
现在我们评估每个区间内导数的符号，以确定函数是递增还是递减。因此，我们在每个区间取一个点（不是临界点），并查看此时导数的符号：

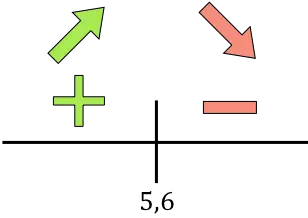
$A'(0)=\cfrac{160-16\cdot 0-8\pi \cdot 0 }{16} +\cfrac{16\pi \cdot 0}{64} = 10 +0 = 10 \ \rightarrow \ \bm{+}$

$A'(6)=\cfrac{160-16\cdot 6-8\pi \cdot 6 }{16} +\cfrac{16\pi \cdot 6}{64} = -5,42 +4,71 = -0,71 \ \rightarrow \ \bm{-}$

如果导数为正，则表示函数在增，如果导数为负，则表示函数在减。因此，增长区间和下降区间为：

生长：

$\bm{(-\infty , 5,6)}$

减少：

$\bm{(5,6,+\infty)}$

该函数在 x=5.6 处从增加变为减少，因此x=5.6 是该函数的最大值。

然而，

$x=5,6$

是形成最大表面的值。现在我们计算的值

$y :$

$y = \cfrac{40-2\cdot 5,6- \pi \cdot 5,6}{4} = 2,80$

因此，构成最大表面积的值为：

$\bm{x = 5,60} \ \mathbf{m}$

$\bm{y = 2,80} \ \mathbf{m}$

问题6

我们要建造一个面积为54 cm ²的圆柱形水箱。确定圆柱体的底面半径和高度，使体积最大。

查看解决方案

步骤1：设置要优化的功能。

圆柱体的体积用以下公式计算：

$V= A_{base}\cdot h$

底面积是圆，所以它的公式是

$A_{\text{base}}=\pi r^2$

。因此，圆柱体的体积公式为：

$V= \pi r^2 \cdot h$

我们已经有了优化的功能。但这取决于两个变量（

$r$

和

$h$

），而它只能依赖于一个。然而，声明告诉我们，圆柱体的面积必须是 54 cm ² ，所以我们要利用这个条件来找到之间的关系

$r$

和

$h .$

要计算圆柱体的面积，必须将其侧面积与两个底面的面积相加：

$A_{cilindro} = A_{lateral}+2A_{base} = 2\pi r h + 2\pi r^2$

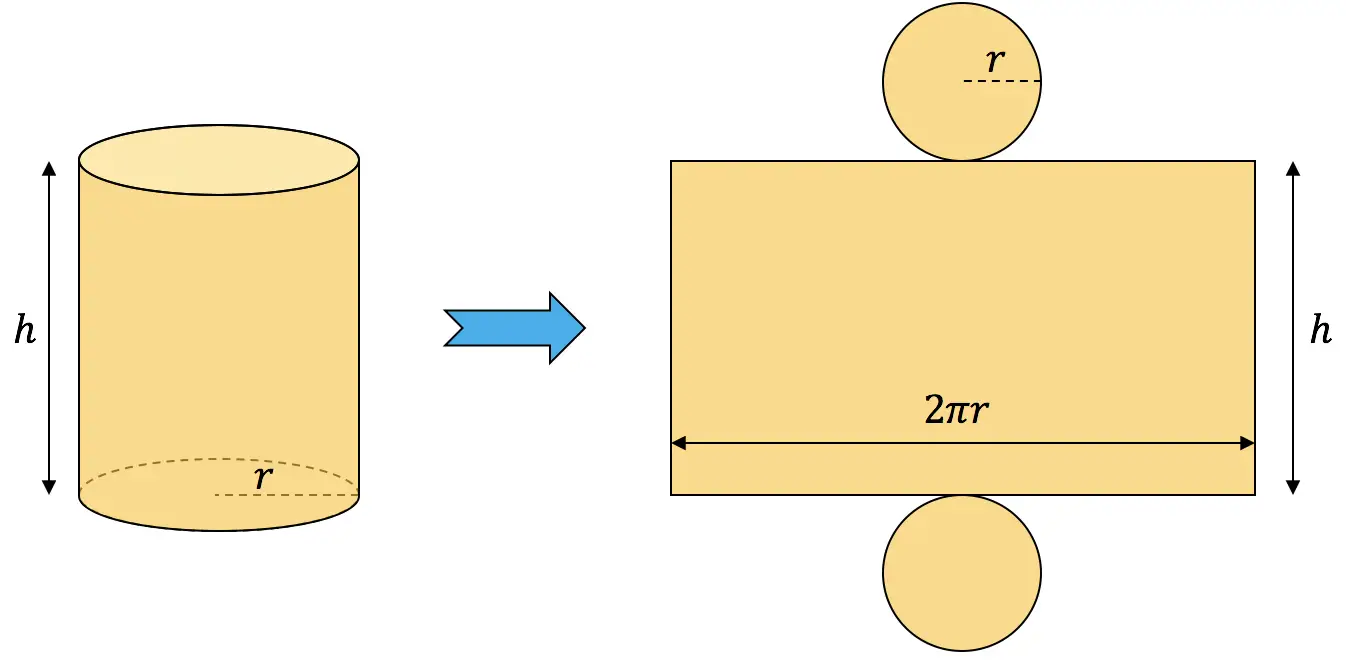
圆柱体的面积必须为54 cm ² ，因此我们将前面的表达式设置为等于54，以获得之间的关系

$r$

和

$h :$

$A_{cilindro} =2\pi r h + 2\pi r^2 = 54$

我们清除

$h :$

$2\pi r h = 54 - 2\pi r^2$

$h = \cfrac{54 - 2\pi r^2}{2\pi r}$

我们替换在要优化的函数中找到的表达式：

$V= \pi r^2 \cdot h \xrightarrow{h \ = \ \frac{54 - 2\pi r^2}{2\pi r} } V = \pi r^2 \cdot \cfrac{54 - 2\pi r^2}{2\pi r}$

$V = \cancel{\pi} r^{\cancel{2}} \cdot \cfrac{54 - 2\pi r^2}{2 \cancel{\pi} \cancel{r}} =r \cdot \cfrac{54 - 2\pi r^2}{2}$

$V(r) = r \cdot (27 - \pi r^2)= 27r - \pi r^3$

步骤2：计算待优化函数的导数。

$V(r)=27r - \pi r^3\ \longrightarrow \ V'(r)= 27-3 \pi r^2$

第三步：找到关键点。

为了找到函数的临界点，我们求解

$V'(r)=0:$

$V'(r)=0$

$27-3 \pi r^2=0$

$-3 \pi r^2=-27$

$r^2=\cfrac{-27}{-3\pi }$

$r^2=2,86$

$\sqrt{r^2}=\sqrt{2,86}$

$r=1,69$

步骤4：研究函数的单调性并确定函数的最大值或最小值。

为了研究函数的单调性，我们表示在数轴上找到的临界点：

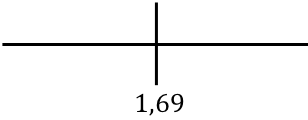
现在我们评估每个区间内导数的符号，以确定函数是递增还是递减。因此，我们在每个区间取一个点（不是临界点），并查看此时导数的符号：

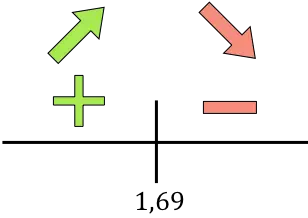
$V'(0)= 27-3 \pi\cdot 0^2 = 27-0 = +27 \ \rightarrow \ \bm{+}$

$V'(2)= 27-3 \pi \cdot 2^2 = 27-37,70 = -10,70 \ \rightarrow \ \bm{-}$

如果导数为正，则表示函数在增，如果导数为负，则表示函数在减。因此，增长区间和下降区间为：

生长：

$\bm{(-\infty,1,69)}$

减少：

$\bm{(1,69,+\infty)}$

该函数在 r=1.69 时从增加变为减少，因此r=1.69 cm 是该函数的最大值。

因此，r=1.69是使体积达到最大的半径值。现在我们计算高度：

$h = \cfrac{54 - 2\pi \cdot 1,69^2}{2\pi \cdot1,69} = \cfrac{54 - 17,94}{10,62} = 3,39$

因此，使最大音量的值是：

收音机

$\bm{= r = 1,69} \ \mathbf{cm}$

高度

$\bm{= h = 3,39} \ \mathbf{cm}$

什么是优化问题？

如何解决优化问题

优化问题的示例

优化问题已解决

问题1

问题2

问题3

问题4

问题5

问题6

发表评论 取消回复

发表评论取消回复