本页解释什么是无理函数(也称为根式函数),以及此类函数的所有特征。您还将了解如何计算根函数或无理函数的域,此外,您将能够了解如何通过示例在图表上表示它们,并通过练习和逐步解决的问题进行练习。
什么是无理(或激进)函数?
无理函数与根式函数的含义相同,因此它们共享一个定义:
无理函数,也称为根式函数,是自变量 x 位于根符号下的函数。
我们已经知道,根的结果可以是正的,也可以是负的。因此,无理(或根式)函数的表示有两条可能的曲线:
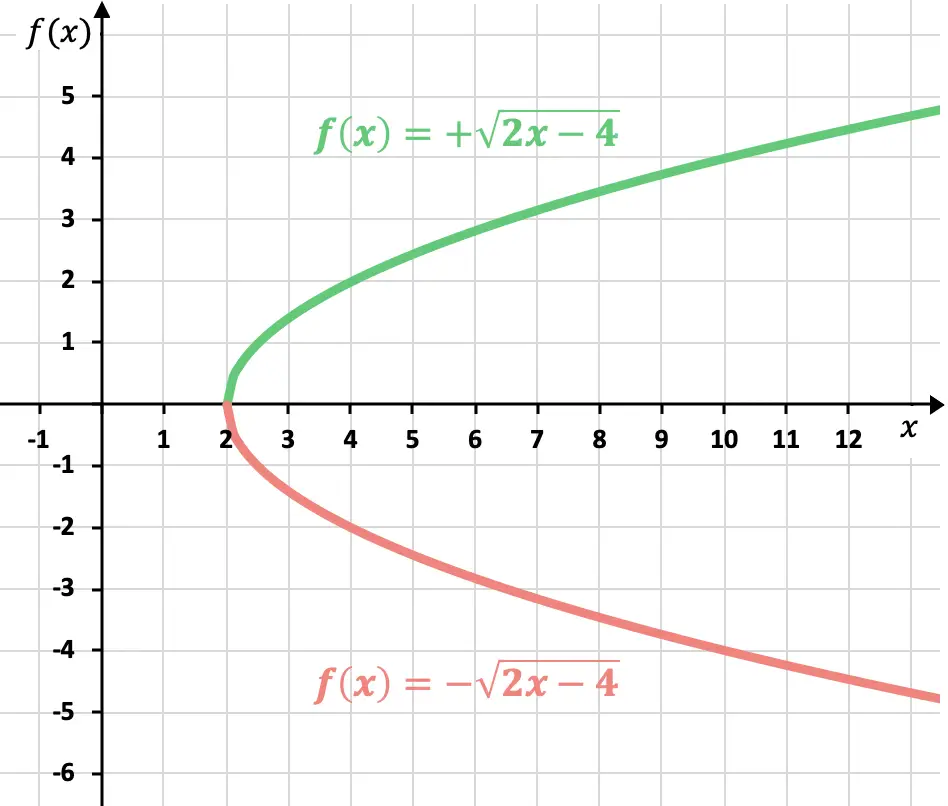
但如果没有指定符号,则应该表示正函数。
另一方面,无理函数不应与有理函数混淆。尽管它们的名称非常相似,但它们是两种完全不同类型的函数。
无理函数或根式函数的定义域
有根函数的定义域取决于根索引的奇偶性,即取决于根索引是偶数还是奇数。
具有偶数索引根的函数的域
众所周知,负数没有根(偶数索引)。因此,只要其内容等于或大于0,偶索引的根式函数就存在。
作为示例,让我们看看如何计算以下根式或无理函数的域:
![]()
这是一个激进的偶指数函数,所以我们必须看看它的内容何时为正或为零:
![]()
我们解决不等式:
![]()
因此,只要 x 大于或等于 4,该函数就会存在,并由以下区间表示:
![]()
根为奇数索引的函数的域
具有奇数索引的无理函数不存在此问题,因为存在负数的奇数索引根:
![]()
因此,对于任何x值,都存在奇索引的根函数。或者,换句话说,域仅由实数组成。
例如,我们将计算以下索引为奇数的根式函数的定义域:
![]()
由于它是一个具有奇数索引的无理函数,因此它的域由实数组成:
![]()
如何表示无理函数或激进函数
让我们通过示例了解如何在图形上表示具有根的函数。
- 在图上绘制以下根函数或无理函数:
![]()
首先要做的是找到函数的定义域。由于它是平方根,因此它包含的任何内容都必须是正数,因为负数不存在平方根。因此,只要根式函数的内容等于或大于0,根式函数就存在:
![]()
![]()
因此,函数的域由所有大于或等于 -2 的数字组成。也就是说:
![]()
一旦我们知道了函数的域,我们就创建一个值表。显然,我们计算的点越多,函数的表示就越精确。但计算域区间内的 3 或 4 个点就足够了:
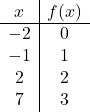
我们现在在图表上表示获得的点:
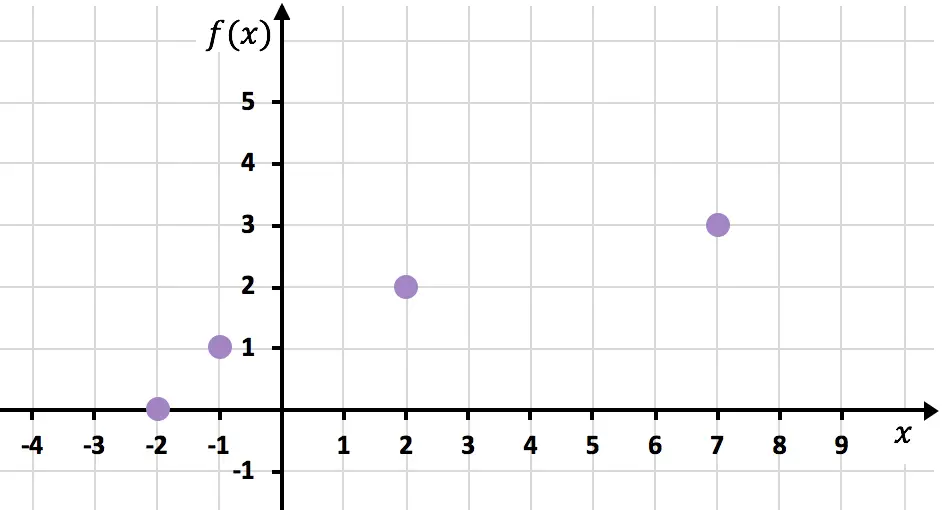
最后,我们连接这些点并延长曲线以表明函数继续增长:
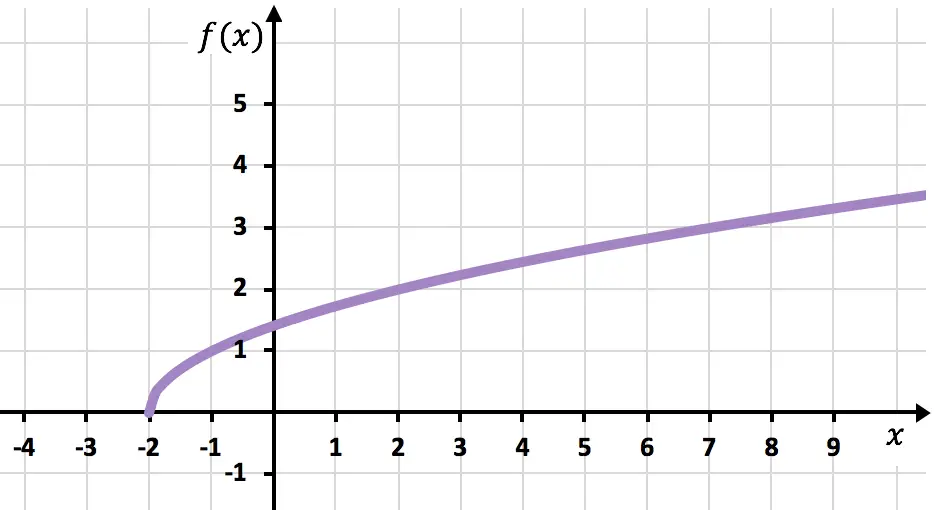
解决了无理函数或激进函数的练习
练习1
求下列根式函数的定义域:
![]()
负数的平方根不存在。因此,当根参数为正或零时,该函数将存在:
![]()
![]()
![]()
![]()
![]()
练习2
求下列无理函数的定义域:
![]()
负数的平方根没有实数解。因此,只要根的内容为正或零,该函数就存在:
![]()
![]()
![]()
请记住,如果在不等式中我们改变乘法或除法负数的两边,我们还必须旋转不等式的符号。
![]()
![]()
练习3
在图上绘制以下无理函数:
![]()
首先,我们必须计算函数的定义域:
![]()
![]()
![]()
现在我们通过给出域范围内的函数值来创建一个值数组:
![]()
![]()
![]()
![]()

最后,我们绘制点并将函数绘制在图上:
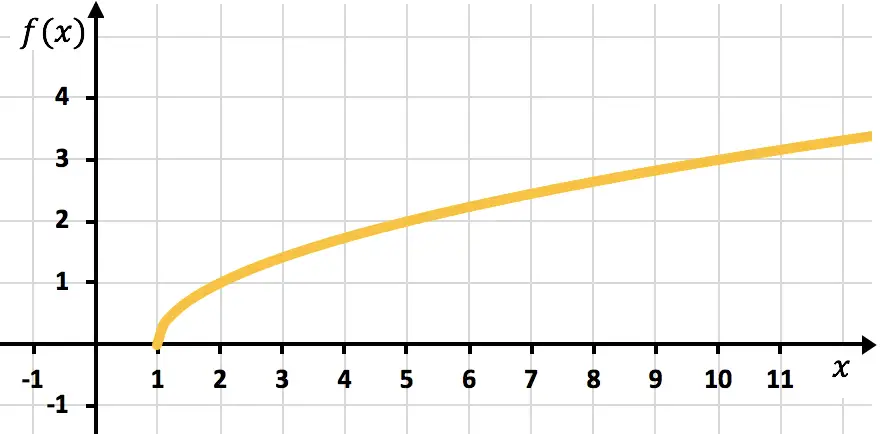
练习4
绘制以下无理函数或根式函数的图像:
![]()
首先,我们必须计算函数的定义域:
![]()
![]()
现在我们通过给出域范围内的函数值来创建一个值数组:
![]()
![]()
![]()
![]()

最后,我们绘制点并在图上绘制函数:
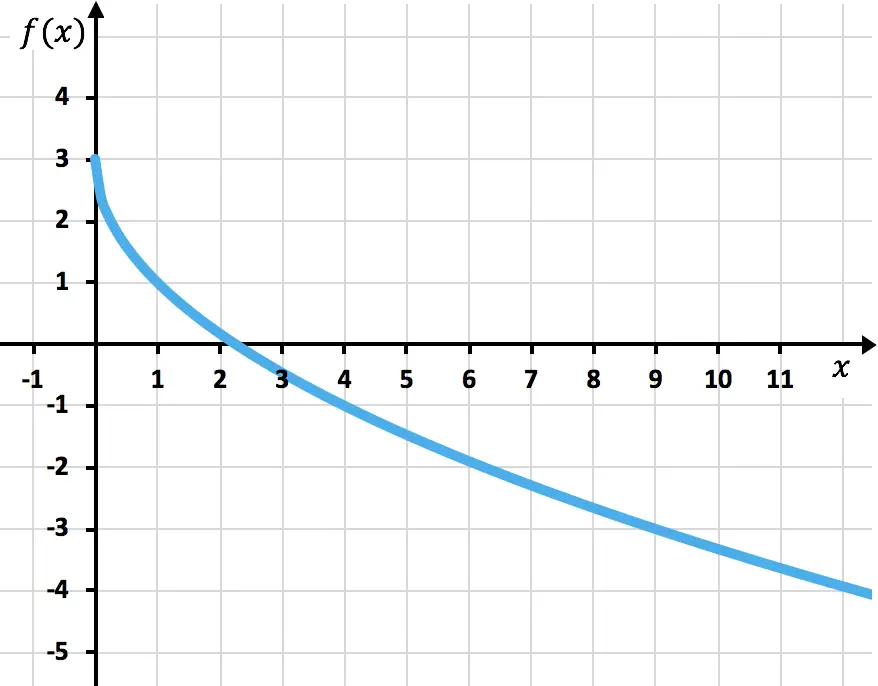
练习5
绘制以下无理函数或根式函数的图像:
![]()
在绘制函数之前,我们需要计算函数的域:
![]()
![]()
![]()
请记住,如果在不等式中我们改变了乘法或除法负数的两边,我们也必须改变不等式的符号。
![]()
![]()
现在我们通过在属于函数域的点处评估函数来构造一个值表:
![]()
![]()
![]()
![]()

最后,仅表示点并将函数绘制在图表上:
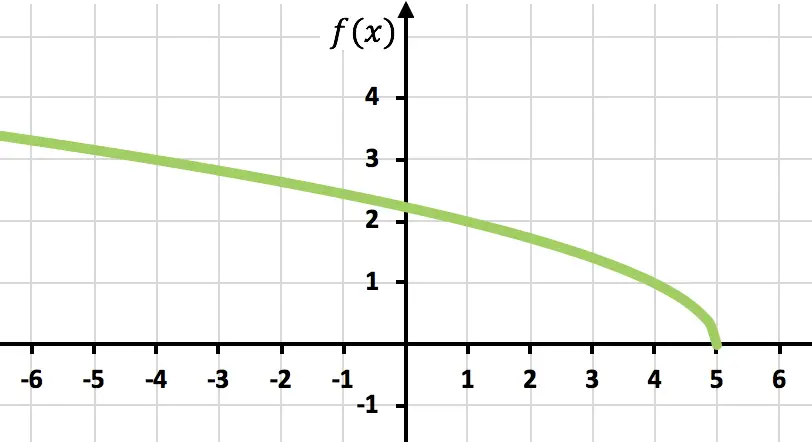
练习6
在图上绘制以下无理函数或根式函数:
![]()
我们首先要计算函数的定义域:
![]()
在这种情况下,我们得到了二阶不等式,因此我们需要应用二次方程公式来求解:
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3e5bc09c561e2790b1af96a618a015a0_l3.png)
我们将线分成三段并获得根:

我们用一个数字代替不等式的每个部分,看看哪些部分满足不等式,因此属于该域:
![x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”></p>
</p>
<p>❌</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9c9c5a39dc152cdcb902dbf0b2e5b59_l3.png)
![]()
![]()
✅
因此,尊重不等式的部分是边的部分:

因此,函数的定义域为:
![]()
一旦我们计算了函数的域,我们就构建一个值表,给出函数在域区间内的值:
![]()
![]()
![]()
![]()
![]()
![]()

最后,我们将获得的点表示在图上并绘制函数:
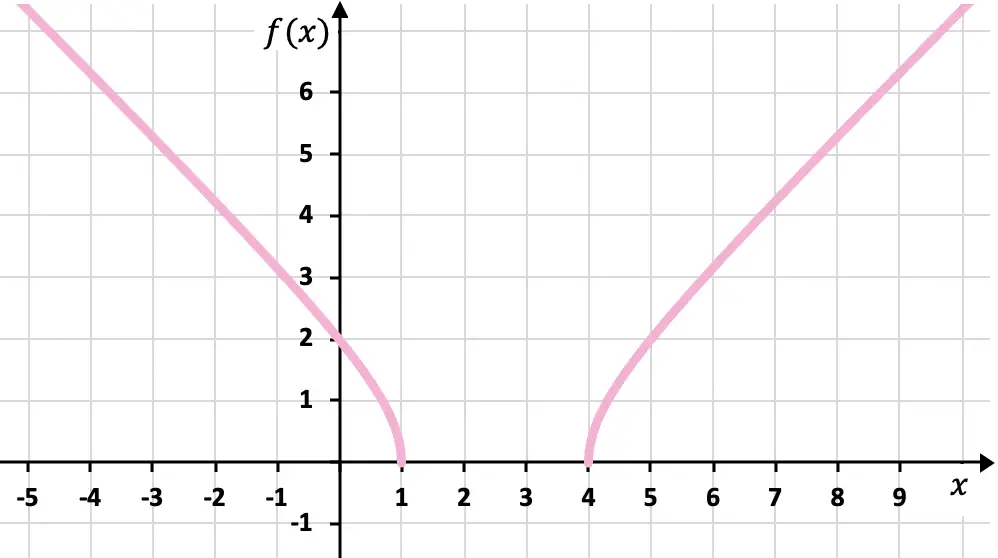
练习7
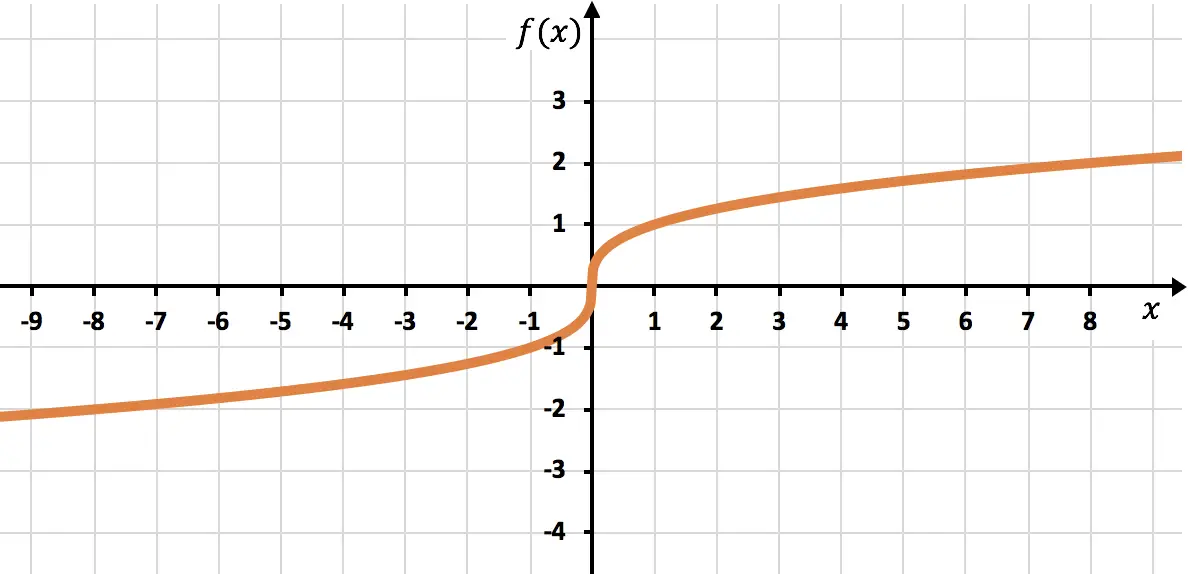
在图上表示由根形成的以下函数:
![]()
它是一个无理函数,其根具有奇数索引,因此函数的域由实数组成:
![]()
因此,我们可以取任意点来创建值表。在这种情况下,我们将寻找许多点,因为它是立方根:
![]()
![]()
![]()
![]()
![]()
![]()
![]()

最后,我们绘制找到的点并将函数绘制在图上:
练习8
解决以下与无理(或激进)函数相关的问题:
手机电池的消耗由以下函数给出:
![]()
其中消耗量以毫安 (mA) 表示,
![]()
是经过的时间(以分钟为单位)。
确定常数的值
![]()
4 分钟后消耗电流为 35 mA。
4 分钟后消耗为 35 mA,意味着当 t 为 4 时,f(t) 为 35。因此 f(4)=35。
![]()
![]()
现在我们需要求解我们得到的方程。如果你仔细观察,就会发现这是一个无理方程,因为它有根。在此类方程中,首先要做的是隔离一侧的根,在本例中该根已经被隔离。一旦分离出来,我们必须对方程两边求平方:
![]()
然后我们化简根:
![]()
我们求解方程:
![]()
![]()
![]()
最后,在无理方程中,必须验证解。因此,我们必须在开头的方程中代入 K=-1221:
![]()
![]()
![]()
![]()
由于满足等式,所以 K=-1221 是解。